P1608 路径统计
考察:最短路
思路:
dist[v]表示到v的最短距离,cnt[v]表示达到v最短距离条数.dijkstra算法里,一旦v出队,那么它的最短距离就已经确定了.因为到达点v的最短距离,一定比当前点再去扩展的距离小.所以这道题不需要担心重复遍历点v,使得此路径后面的点方法数全部+1
这里注意相同起点终点权值相同的路径算一条.
1 #include <iostream> 2 #include <cstring> 3 #include <queue> 4 #include <set> 5 using namespace std; 6 typedef pair<int,int> PII; 7 const int N = 2010; 8 bool st[N]; 9 int n,m,idx,h[N],dist[N],cnt[N]; 10 set<PII> s; 11 struct Road{ 12 int fr,to,ne,w; 13 }road[N*N]; 14 void add(int a,int b,int w) 15 { 16 road[idx].w = w,road[idx].to = b,road[idx].ne = h[a],h[a] = idx++; 17 } 18 void dijkstra() 19 { 20 memset(dist,0x3f,sizeof dist); 21 priority_queue<PII,vector<PII>,greater<PII> > q; 22 dist[1] = 0; cnt[1] = 1; 23 q.push({0,1}); 24 set<PII> s; 25 while(q.size()) 26 { 27 PII it = q.top(); 28 q.pop(); 29 int di = it.first,u = it.second; 30 if(st[u]) continue; 31 st[u] = 1; 32 s.clear(); 33 for(int i=h[u];i!=-1;i=road[i].ne) 34 { 35 int v = road[i].to,w = road[i].w; 36 if(!s.count({v,w})) s.insert({v,w}); 37 else continue; 38 if(dist[v]>dist[u]+w) 39 { 40 dist[v] = dist[u]+w; 41 cnt[v] = cnt[u]; 42 q.push({dist[v],v}); 43 }else if(dist[v]==dist[u]+w) cnt[v]+=cnt[u],q.push({dist[v],v}); 44 } 45 } 46 } 47 int main() 48 { 49 scanf("%d%d",&n,&m); 50 memset(h,-1,sizeof h); 51 while(m--) 52 { 53 int x,y,z; 54 scanf("%d%d%d",&x,&y,&z); 55 add(x,y,z); 56 } 57 dijkstra(); 58 if(cnt[n]) printf("%d %d\n",dist[n],cnt[n]); 59 else puts("No answer"); 60 return 0; 61 }
这道题里面学问太多了....补一下知识点:
1.这道题不能直接用SPFA.反例如图:
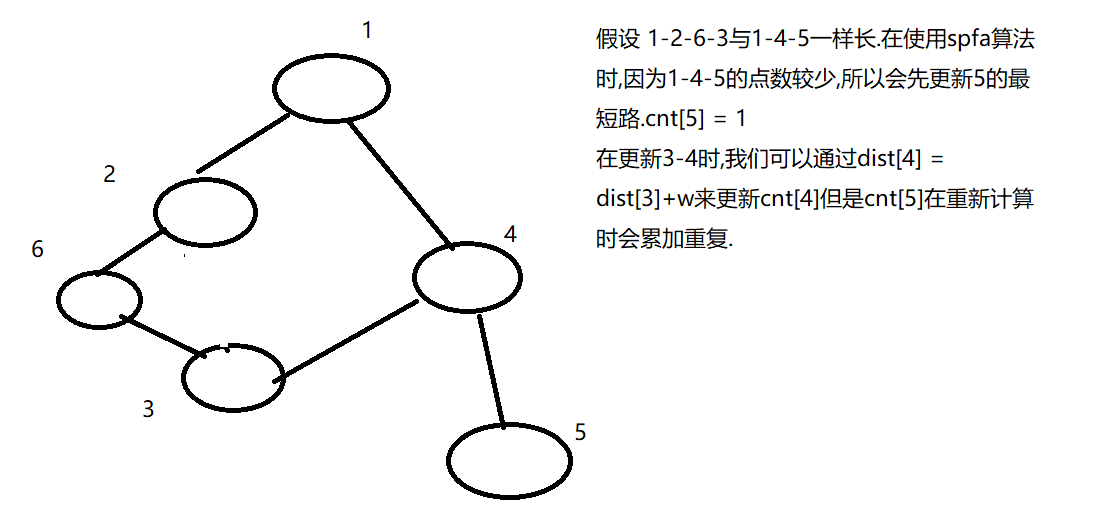
2.但这道题可以间接用SPFA算法.我们知道最短路有点类dp,而这道题实际是最优解的方案数.背包问题中我们对最优解的求法是先求出最小值是多少,然后再将所有能推到最优解的子状态累加,但这建立在拓扑序上完成,而图论问题一般有环,直接递推难以求解.所以也要具有拓扑序的图上求解.
BFS每个点只进队一次,每次都是按边的数量扩展,在边权只有1的情况下,它每次扩展都是扩展比上一层距离更远的点,因此BFS是满足拓扑序的.
Dijkstra算法,每个点只出队一次,每次都是优先扩展当前距离更小的点,再用这个点去更新其他点.每次扩展都是比上一层扩展距离更大.
SPFA算法就不能保证拓扑序,因为它每个点都可能进队出队多次.但是如果我们先跑一遍SPFA,建立有拓扑序的图,再求一遍就可以保证正确答案.
