[ZJOI2019]线段树 - 线段树、dp
Description
现在可怜手上有一棵 \([1,n]\) 上的线段树,编号为 \(1\)。这棵线段树上的所有节点的 \(tag\) 均为 \(0\)。接下来可怜进行了 \(m\) 次操作,操作有两种:
-
\(1\ l\ r\),假设可怜当前手上有 \(t\) 棵线段树,可怜会把每棵线段树复制两份(\(tag\) 数组也一起复制),原先编号为 \(i\) 的线段树复制得到的两棵编号为 \(2i-1\) 与 \(2i\),在复制结束后,可怜手上一共有 \(2t\) 棵线段树。接着,可怜会对所有编号为奇数的线段树进行一次 \(\operatorname{Modify}(root,1,n,l,r)\)。
-
\(2\),可怜定义一棵线段树的权值为它上面有多少个节点 \(tag\) 为 \(1\)。可怜想要知道她手上所有线段树的权值和是多少。
\(n,m \le 10^5.\)
Solution
经过 \(k\) 次复制后,会有 \(2^k\) 棵线段树,但是仔细观察后会发现,这 \(2^k\) 棵线段树对应的正是 \(k\) 次操作集合的所有可能子集。
继续分析,可以发现其实每次操作时,线段树上的点只有四类:
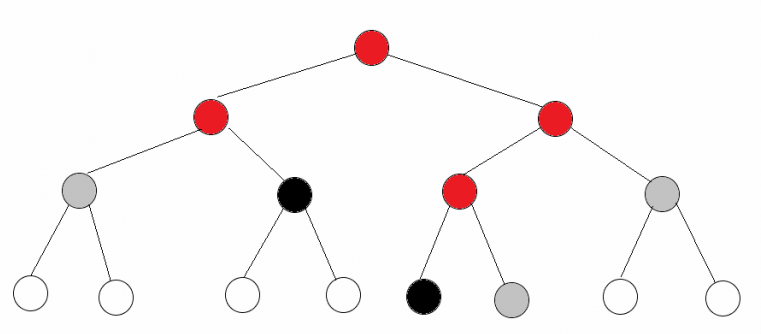
- 红色点:会被访问到,标记被下放的节点
- 黑色点:会被访问并且修改的节点
- 灰色点:会被访问到,未被修改但可能会有标记下放的节点
- 白色点:不会被访问到的点
容易想到一个 \(\text{dp}\),设 \(f_{u,i}\) 为节点 \(u\) 在第 \(i\) 次修改后 \(tag\) 为 \(1\) 的节点的个数,但是这样会发现灰色点无法转移,因为并不知道 \(u\) 到根节点的路径上是否有 \(tag\) 为 \(1\) 的节点,使得其 \(tag\) 能下放到灰色点上。
于是索性将不知道的东西定义成状态,设 \(g_{u,i}\) 表示节点 \(u\) 在第 \(i\) 次修改后从 \(u\) 到根节点的路径上有多少个至少有一个 \(tag\) 为 \(1\) 的点。
下面考虑如何进行转移:
-
红色点: 有一半点的标记会被下放,所以 \(f\) 不变,同时由于红色点到根路径的所有点标记都会被下放,所以 \(g\) 也不变。
\[\begin{cases} f_{u,i} = f_{u,i-1} \\ g_{u,i} = g_{u,i-1} \\ \end{cases} \] -
黑色点: 因为有一半的点会被修改,因此 \(f,g\) 的贡献都翻倍。
\[\begin{cases} f_{u,i} = f_{u,i-1} + 2^{i-1} \\ g_{u,i} = g_{u,i-1} + 2^{i-1} \\ \end{cases} \] -
灰色点: 这类点需要到根路径有 \(tag\) 为 \(1\) 的点才能被下放从而使自身的 \(tag\) 变为 \(1\),所以 \(f\) 直接利用 \(g\) 转移即可,而 \(g\) 本身并无变化,但由于线段树翻倍的影响,也随之翻倍。
\[\begin{cases} f_{u,i} = f_{u,i-1} + g_{u,i-1} \\ g_{u,i} = g_{u,i-1} + g_{u,i-1} \\ \end{cases} \] -
白色点: 这类点没有进行任何操作,所以 \(f,g\) 直接随着线段树翻倍而翻倍即可。
\[\begin{cases} f_{u,i} = f_{u,i-1} + f_{u,i-1} \\ g_{u,i} = g_{u,i-1} + g_{u,i-1} \\ \end{cases} \]
前三类点一次都可以在 \(O(\log n)\) 的内修改完成,而第四类点的一次修改是 \(O(n)\) 的,所以还需要打标记。


