AGC005D ~K Perm Counting - dp、计数

Desciption

如果一个排列 \(P\) 满足对于所有的 \(i\) 都有 \(|Pi-i|\ne k\)，则称排列 \(P\) 为合法的。现给出排列长度 \(n\) 和 \(k\)，求有多少种合法的排列，答案 \(924844033\) 取模。

Solution

考虑将排列放到棋盘上。例如 \(n=6,k=2\) 时，如下图所示，红色是不能选择的格子。

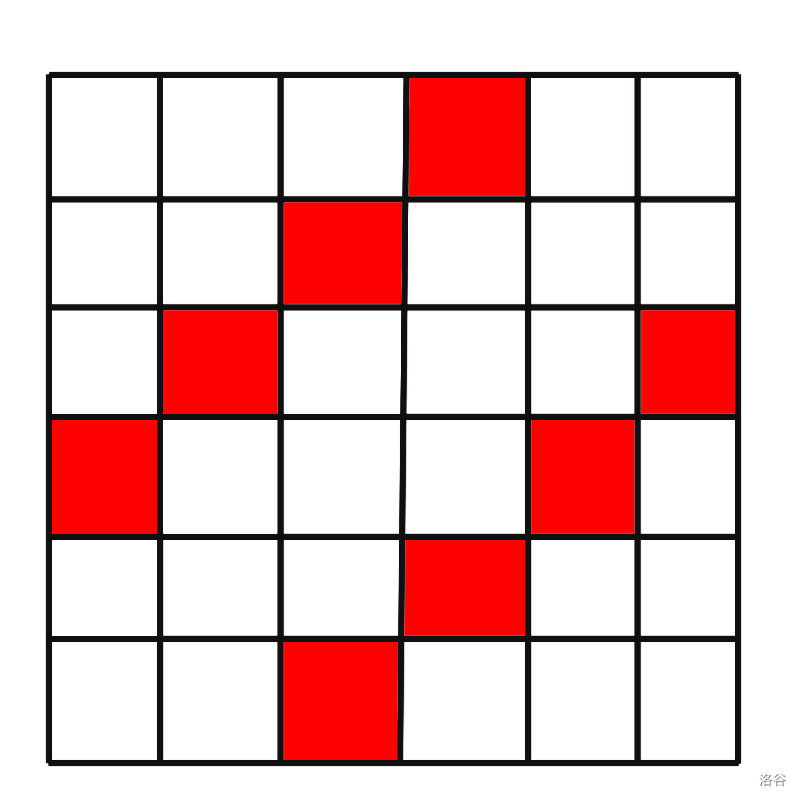然后由于合法的方案不太好计算，考虑容斥，计算不合法的方案。

设 \(f_i\) 表示选了 \(i\) 个不合法的数的方案数，答案即为

\[\sum \limits_{i=0}^{n} (-1)^i f_i (n-i)! \]

发现相互冲突的格子之间形成了 \(2k\) 条链，且链与链之间是相互独立的，于是我们可以把这些链拼起来，进行 \(dp\)。

设 \(f_{i,j,0/1}\) 表示前 \(i\) 个点，选了 \(j\) 条边，当前这个点与前面的点连边/不连边的方案数，则

\[f_{i,j,0} = f_{i-1,j,0} + f_{i-1,j,1} \\f_{i,j,1} = f_{i-1,j-1,0},i与i-1在同一条链上 \]

注意选择的点不能在同一行或同一列，也就是说在同一条链上不能有两个点相邻。

时间复杂度 \(O(N^2)\)，可以用生成函数和 \(NTT\) 优化到 \(O(N\log N)\)，但我太菜了，不会。

Code

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const int _ = 4e3 + 10;
const ll mod = 924844033;
int tot, N, K, edge[_];
ll f[_][_][2], fac[_], ans = 0;

int main() {
#ifndef ONLINE_JUDGE
	freopen("count.in", "r", stdin);
	freopen("count.out", "w", stdout);
#endif
	scanf("%d%d", &N, &K);
	fac[0] = 1;
	for (int i = 1; i <= N; ++i) fac[i] = fac[i - 1] * i % mod;
	for (int i = 1; i <= K; ++i)
		for (int t = 1; t <= 2; ++t)
			for (int j = i; j <= N; j += K) {
				++tot;
				if (j != i) edge[tot] = 1;
			}
	f[0][0][0] = 1;
	for (int i = 1; i <= N * 2; ++i) {
		for (int j = 0; j <= i / 2; ++j) {
			f[i][j][0] = (f[i][j][0] + f[i - 1][j][0] + f[i - 1][j][1]) % mod;
			if (edge[i] && j > 0) f[i][j][1] = (f[i][j][1] + f[i - 1][j - 1][0]) % mod;
		}
	}
	ll p = 1;
	for (int i = 0; i <= N; ++i) {
		ans = (ans + p * (f[N * 2][i][0] + f[N * 2][i][1]) % mod * fac[N - i] % mod + mod) % mod;
		p *= -1;
	}
	printf("%lld\n", ans);
	return 0;
}