c4w4_人脸识别和神经风格转换

特殊应用：人脸识别和神经风格转换

人脸识别

与人脸识别（Face Recognition）相关的还有活体检测（Liveness Detection）问题，在这里仅讨论前者。

人脸验证（Face Verification）和人脸识别（Face Recognition）的区别:

• 人脸验证：一般指一个1对1的问题，只需要验证输入的人脸图像是否与某个已知的身份信息对应；
• 一个更复杂的1对多的问题，需要验证输入的人脸图像是否与多个已知身份信息的某一个匹配。

一般来说，对于人脸验证可能只需要达到99%准确率就很好了；而对于人脸识别，如果匹配一张一张图片的正确概率是0.99，直到第一百次才识别到的正确大概率就是0.99¹⁰⁰，所以正确识别的概率就低了，因此就需要高单张图片匹配的准确率。

先学习人脸验证，当人脸验证正确率很高之后就可以应用到人脸识别。

One-shot学习

人脸识别所面临的一个挑战是要求系统之采集一次面部样本，就可以快速准确地识别出身份信息。即只用一个训练样本来获得准确的预测结果。这就被称为One-shot learning。

如果需要建立一个四人的人脸识别系统，根据我们前面学到的，可能想到可以建立一个卷积网络，最后用softmax输出四个类别，代表四个人。但是由于每个人可能只有一张照片作为训练集，训练出来的网络效果可能比较差。而且当要添加新的身份信息的时候，就需要重新训练模型，显然这不是个好的办法。

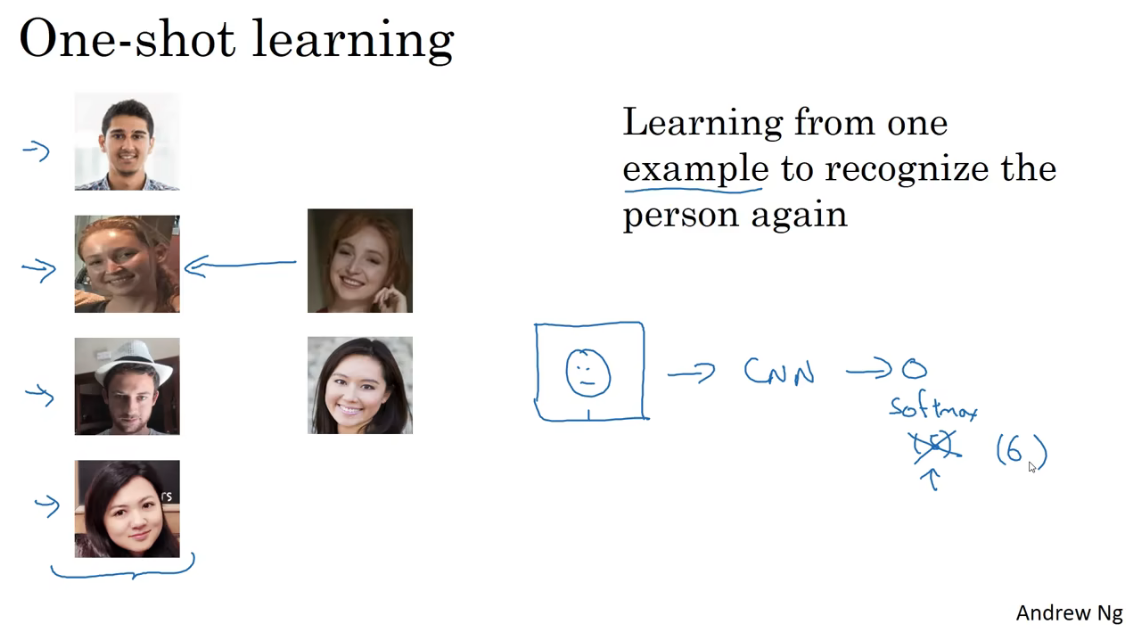
所以，为了更好的效果，网络需要学习的是一个相似Similarity函数，代表两张图片的差异度。如下图所示。当大于等于阈值$\tau$，表示为同一人；当小于$\tau$，就代表是不同的人。

Siamese 网络

实现上述Similarity函数的一种方式就是使用Siamese网络，它是一种对两个输入运行相同的卷积网络，然后对两个输出结果进行比较的网络结构。

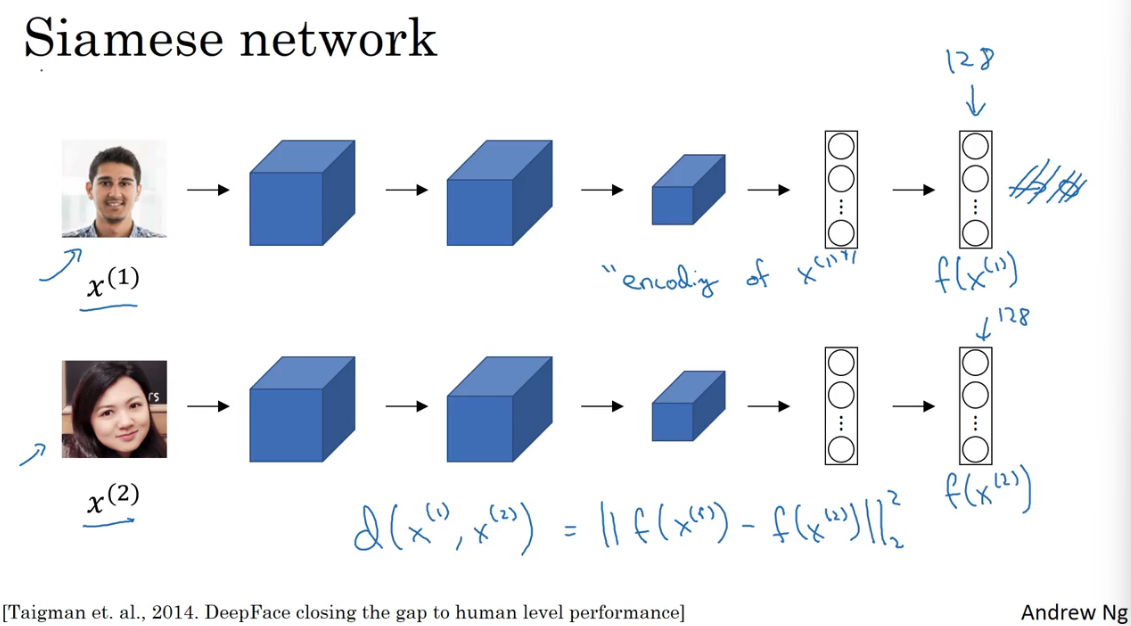
如上图中的示例，在最后的全连接层我们不用Softmax输出，而是直接得到两个特征向量$f(x^{(1)})$、$f(x^{(2)})$，称他们为$x^{(1)}$ 、$x^{(2)}$的编码。并将$x^{(1)}$ 、$x^{(2)}$的距离定义为两个编码之差的L2范数，即$d((x^{(1)}),x^{(2)})=||fx^{(1)}-fx^{(2)}||_2^2$ ，这就是Siamese网络架构。

把上面的定义推广一下就得到了图片中的对$x^{(i)}$ 、$x^{(j)}$的式子，用于人脸识别。

Triplet损失

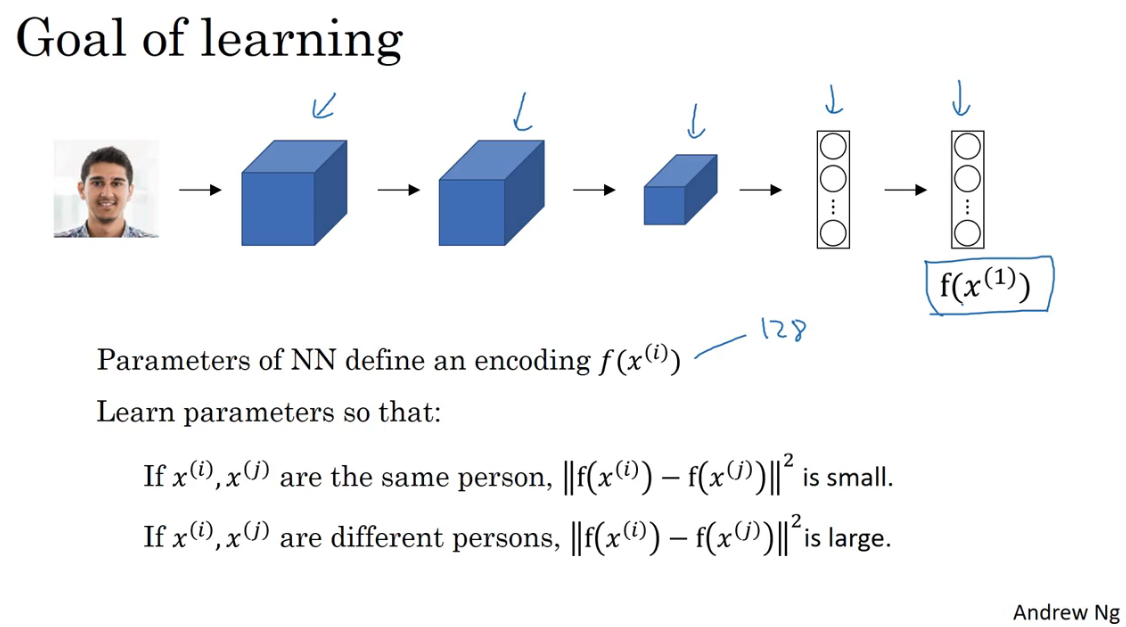
想要通过训练神经网络的参数，达到Siamese网络获得到质量人脸编码的目标，方法之一就是定义三元组损失函数然后应用梯度下降。

为了定义Triplet Loss，需要把数据给定义成三元组的形式。即用于训练的数据是包含Anchor（靶目标）、Positive（正例）、Negative（反例）这样的三元图片组。这也是Triplet这一词的含义。

Anchor和Positive是同一人脸，Anchor与Negative是不同的人。对于三元组分别取首字母代称，即A、P、N。

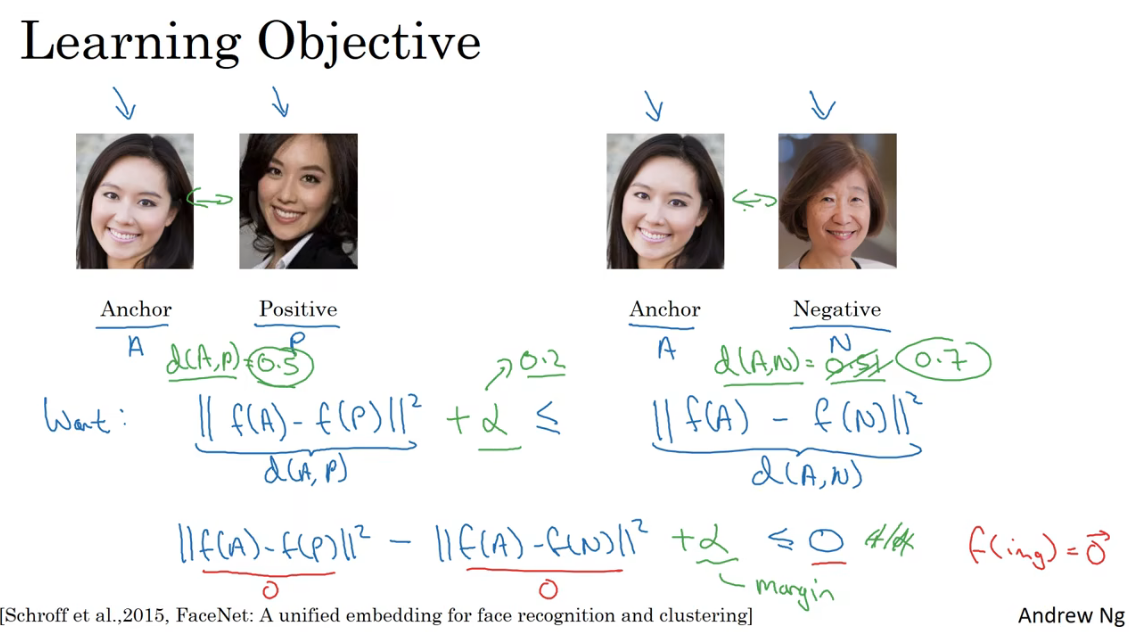
对于这样的三张图片，应该有下面所示的

$$||f(A)-f(P)||^2 + \alpha \leq ||f(A)-f(N)||^2$$

其中，$\alpha$被称为间隔(margin)他是一个超参数，用来确保当函数$f(x)$总是输出0或者恒定值时，不等式不成立。

上面的不等式表示训练好的神经网络输出对图片的编码要满足A和P的差异应当小于A和N的差异。如果没有间隔α，当网络输出图像的编码为0或为恒值时，满足A、P、N的差异要求，但是显然这种网络不是我们期望的，是无效的结果。因此引入了间隔超参数α

当满足上述不等式是，认为对人脸识别的预测就是准确的，损失就为0；不满不等式时，预测不准确，所以损失就应该是$||f(A)-f(P)||^2 + \alpha - ||f(A)-f(N)||^2$这个大于0的数字。

所以，Triplet损失函数的定义：

$$L(A,P,N)=max(||f(A)-f(P)||^2 + \alpha - ||f(A)-f(N)||^2,0)$$

那么，对于大小为$m$的训练集，代价函数为：

$$J=\sum_{i=1}^mL(A^{(i)},P^{(i)},N^{(i)})$$

通过梯度下降优化代价函数。

对于训练样本A、P、N的选择要说明的一点是，如果随机选择很容易的导师A和P非常相似，A和N差异巨大，所以很容易满足$d(A,P)+\alpha \leq d(A,N)$，导致训练出来的神经网络可能效果较差。

因此，应该选择 $$d(A,P)+\alpha \approx d(A,N)$$ 的三元组，促使模型学习不同人脸之间的关键差异。可以的做法是，人为增加 Anchor 和 Positive 的区别，缩小 Anchor 和 Negative 的区别。

二分类结构

除了Triplet Loss 以外，二分类结构也可以应用于人脸识别问题中的参数学习。与Triplet Loss不同，二分类结构输入的训练数据是两张图片，如果是同一人y=1，不是y=0。

二分类结构的具体做法是，输入两张图片，将由Siamese 网络产生的两张图片的编码作为输入，传递给同一个sigmoid单元，输出预测值。

Sigmoid单元对应的表达式为

$$\hat y = \sigma(\sum_{k=1}^k w_k|f(x^{(i)}_k)-f(x^{(j)}_k)|+b）$$

其中$w_k$和$b$是通过梯度下降算法迭代训练的参数，和在Siamese 网络中训练的参数是一套参数，绑定在一起的。

上述的表达式中处理两个图片编码的公式还可以替换成其他公式。

$$\hat y = \sigma(\sum_{k=1}^k w_k|\frac{(f(x^{(i)}_k)-f(x^{(j)}_k))^2}{f(x^{(i)}_k)+f(x^{(j)}_k)}|+b）$$

其中，$\frac{(f(x^{(i)})_k - f(x^{(j)})_k)^2}{f(x^{(i)})_k + f(x^{(j)})_k}$ 被称为 $\chi$方相似度

无论是使用Triplet损失函数的网络，还是二分类结构，可以把Siamese 网络计算好的图片编码输出$f(x)$存在数据库中，这样就不必要存储原始图片了。并且每次进行人脸识别的时候，只用再通过Siamese 网络计算出要检测图片的编码拿去比较输出结果，减少了计算量。

神经风格迁移

神经风格迁移，直观上就是将一张图片的风格应用到另外一张图像的内容上，生成具有其风格图片。

监督学习需要标签(y)，但风格迁移不需要标签(y)，所以是无监督学习。

神经风格迁移的过程涉及到三张图片：Style图片提供风格，Content图片提供内容，Generated Image是生成的图片。接下来将用S、C、G分别代表三种图片。

深度卷积网络在学习什么？

为了理解如何实现神经风格转换，首先要理解在输入图像数据后，一个深度卷积网络的的每一层都从中学到了什么。我们可以借助可视化来做到这一点。

可视化的思路：在神经网络中某一层选择一个神经元，遍历所有的训练样本，选择使得该神经元的激活函数最大限度激活的9块图像区域，使用这9块区域作为这个神经元的可视化输出。以此类推可以，可以可视化所有的神经元。

这里说的每层中的神经元是指卷积层中的每一个卷积核（filter），就拿第一层来举例，卷积核滑过图片，计算和卷积核一样大小的那块区域的卷积，然后把结果写到输出对应的格子。把这些卷积结果给到激活函数后，找这些激活函数值最大的区域是那一块。倒推会原始图片的对应区域，这就是对神经元的可视化。对于更深层的也是找到区域不断倒退到原始图片的对应区域，应该是很复杂。。

对于一层可以选择9神经元来可视化，观察这一层的神经元都学到了那些特征。

我们通过遍历所有的训练样本，找出使该层激活函数输出最大的 9 块图像区域。可以看出，浅层的隐藏层通常检测出的是原始图像的边缘、颜色、阴影等简单信息。随着层数的增加，隐藏单元能捕捉的区域更大，学习到的特征也由从边缘到纹理再到具体物体，变得更加复杂。

代价函数

为了构建神经风格迁移系统，需要为生成的 图片定义代价函数。通过最小化 cost function，来生成图片G。

图片G的需要兼顾内容图片的内容和风格图片的风格，因此代价函数由两部分组成，内容代价函数和风格代价函数。

那么，神经风格迁移生成图片 G 的代价函数如下：

$$J(G) = \alpha \cdot J_{content}(C, G) + \beta \cdot J_{style}(S, G)$$

其中，$\alpha$、$\beta$ 是用于控制相似度权重的超参数，就是希望生成图片更偏向内容还是风格。

神经风格迁移的算法步骤如下：

1. 随机生成图片 G 的所有像素点，得到一个白噪声图；
2. 使用梯度下降算法使代价函数最小化，以不断修正 G 的所有像素点。

需要注意的是，普通cost function优化的结果是网络上的参数，而神经风格转换的代价函数去优化的是随机生成G上的每一个像素点，让G的生成和原始两张图更像。所以这里的代价函数并不会针对某个固定的神经网络。

内容代价函数

上述代价函数包含一个内容代价部分和风格代价部分。我们先来讨论内容代价函数 $J_{content}(C, G)$，它表示内容图片 C 和生成图片 G 之间的相似度。

$J_{content}(C, G)$ 的计算过程如下：

• 使用一个预训练好的 CNN（例如 VGG）；

• 选择一个隐藏层 $l$ 来计算内容代价。$l$ 太小则内容图片和生成图片像素级别相似，$l$ 太大则可能只有具体物体级别的相似。因此，$l$ 一般选一个中间层；

• 设 $a^{(C)[l]}$、$a^{(G)[l]}$ 为 C 和 G 在 $l$ 层的激活，则有：

  $$J\_{content}(C, G) = \frac{1}{2}||(a^{(C)[l]} - a^{(G)[l]})||^2$$

$J_{content}(C, G)$ 越小，$a^{(C)[l]}$ 和 $a^{(G)[l]}$ 越相似。

$a^{(C)[l]}$ 和 $a^{(G)[l]}$ 就相当于在人脸识别那块提到的对输入x的编码，并定义两个编码差的第二范数的平方，来形容其差异度，与这里定义的一模一样。

风格代价函数

如何定义一张图片的风格？当我们看到一张图片，对于风格直观的感受是，图片中大量出现的内容，比如梵高的星夜这幅画，是蓝色、黄色扭曲的漩涡这样的风格。

在卷积网络中，我们用第$l$层不同通道之间激活函数的相关性(Correlation)来描述风格。

不同通道之间的激活函数的相关性代表什么？简单的理解是，对于卷积网络同一层不同通道的激活函数，从对卷积层的可视化可以得知，每一个通道学到了图片的一些特征，比如线条、颜色。如果不同的两个通道之间相关性很高（相似度很高），那也就是说这两个通道学习到的内容有很多相似点（类似的地方），那其实这就是我们对图片风格的直观感受，一些图中都有的相似处，就是风格。

对于下图，红色通道学习到了一些垂直的纹理，黄色通道学到了一些橙色的内容，所以如果每个通道都学习到了橙色的垂直纹理，就说明了图片的风格是橙色带垂直纹理。因为每个通道都学到了相似的内容，所以每个通道的激活函数相关性就高。

可以想想我们上面提到了的夜空那个例子。

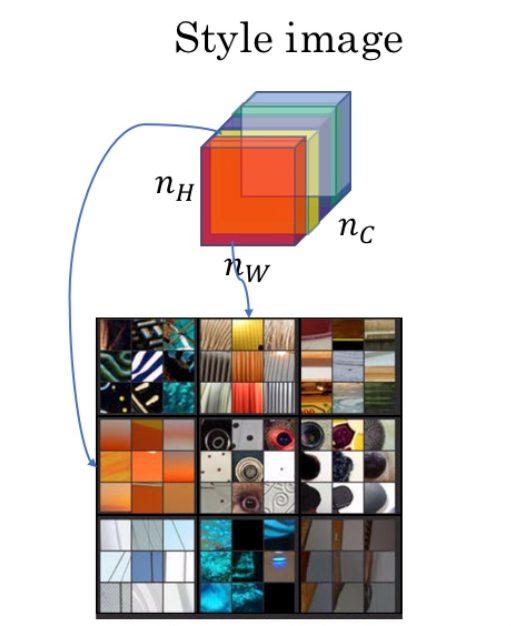
计算两个通道的相关性的具体方法如下：

对于风格图像 S，选定网络中的第 $l$ 层，则相关系数以一个 gram 矩阵的形式表示：

$$G^{[l](S)}_{kk'} = \sum^{n^{[l]}_H}_{i=1} \sum^{n^{[l]}_W}_{j=1} a^{[l](S)}_{ijk} a^{[l](S)}_{ijk'}$$

其中，$i$和 $j$ 为第 $l$ 层的高度和宽度；$k$和 $k^{'}$ 为选定的通道，其范围为 $1$到 $n^{[l]}_C$；$a^{[l](S)}_{ijk}$为激活。

同理对于图像G，有：

$$G^{[l](G)}_{kk'} = \sum^{n^{[l]}_H}_{i=1} \sum^{n^{[l]}_W}_{j=1} a^{[l](G)}_{ijk} a^{[l](G)}_{ijk'}$$

因此，第$l$层的损失函数为：

$$J^{[l]}_{style}(S, G) = \frac{1}{(2n^{[l]}_Hn^{[l]}_Wn^{[l]}_C)^2} || G^{[l](S)}_{kk'} - G^{[l](G)}_{kk^{'}}||^2_F$$

即两个风格矩阵的元素对应相减后求平方和。

$$J^{[l]}_{style}(S, G) = \frac{1}{(2n^{[l]}_Hn^{[l]}_Wn^{[l]}_C)^2} \sum_k^{n^{[l]}_C} \sum_{k'}^{n^{[l]}_C}(G^{[l](S)}_{kk'} - G^{[l](G)}_{kk'})^2$$

如果对求所有层的风格代价函数，效果会更好，所以有：

$$J^{[l]}_{style}(S, G)=\sum_{l}\lambda^{[l]}J^{[L]}_{style}(S,G)$$

其中，$\lambda$ 是用于设置不同层所占权重的超参数。

推广至一维和三维

前面我们学到的卷积网络都是在处理图片，也就是2D数据。时间上卷积网络也可以推广到1D和3D。

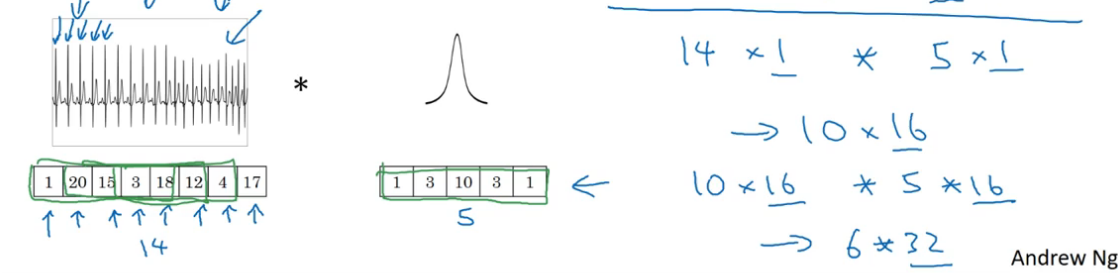
EKG 数据（心电图）是由时间序列对应的每个瞬间的电压组成，是一维数据。一般来说我们会用 RNN（循环神经网络）来处理，不过如果用卷积处理，则有：

• 输入时间序列维度：14 x 1
• 滤波器尺寸：5 x 1，滤波器个数：16
• 输出时间序列维度：10 x 16

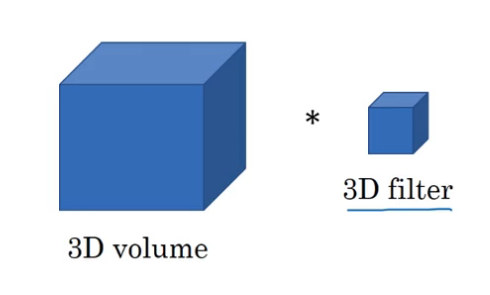
比如CT数据就是3D数据，对人体进行若干层的切片扫描，每层是一张2D的图片，所有图片组成3D数据。此时的输入数据和fitler都是3D的（注意，这里的3D和之前因多个channel画成的3D不一样）

对于三维图片的示例，有

• 输入 3D 图片维度：14 x 14 x 14 x 1
• 滤波器尺寸：5 x 5 x 5 x 1，滤波器个数：16
• 输出 3D 图片维度：10 x 10 x 10 x 16