c1w4_深层神经网络

深层神经网络

什么是深层神经网络？

深层的神经网络（Deep L-layer neural network）就是包含了更多隐藏层的神经网络。

从某种意义上来说，logistic regression可以称为一层的神经网络“1 layer NN”。当计算神经网络的层数，通常将输出层计算在内，而输出层不算，有一个隐藏层，就是2 layer NN，以此类推。当有很多的隐藏层就属于是深层的神经网络。

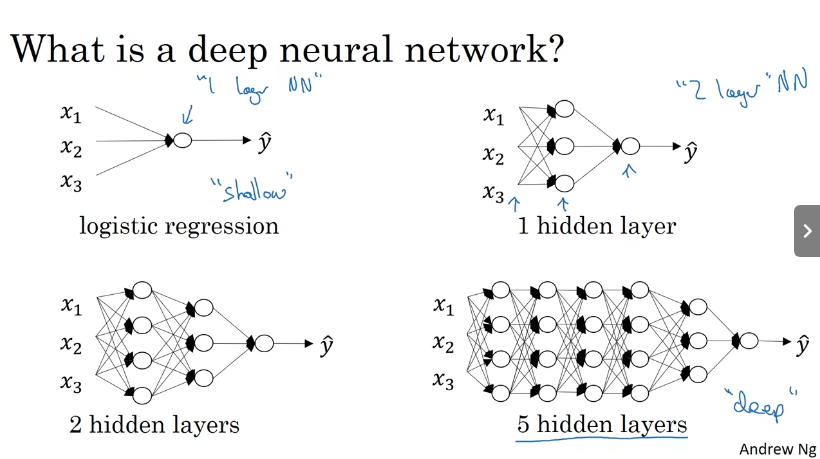
通过复杂的函数构造深层神经网络，可以学习到更多浅层网络模型注意不到的特征。

实际上当面对一些具体问题时，无法事先知道需要多深的神经网络模型。所以可以先试一试logistic regression，然后不断增加隐藏层，根据交叉验证结果取评估具体选择多少隐藏层。所以，可以把隐藏层的数量当作另一个可以自由选择数值大小的超参数。

深层神经网络的符号

深层神经网络的符号，l代表层数，n^[l]代表l层的神经单元个数，a^[l]代表l层的激活函数，W^[l]代表l层的权重参数，b^[l]代表l层的偏置参数。a^[l]=g^[l](z^[l])

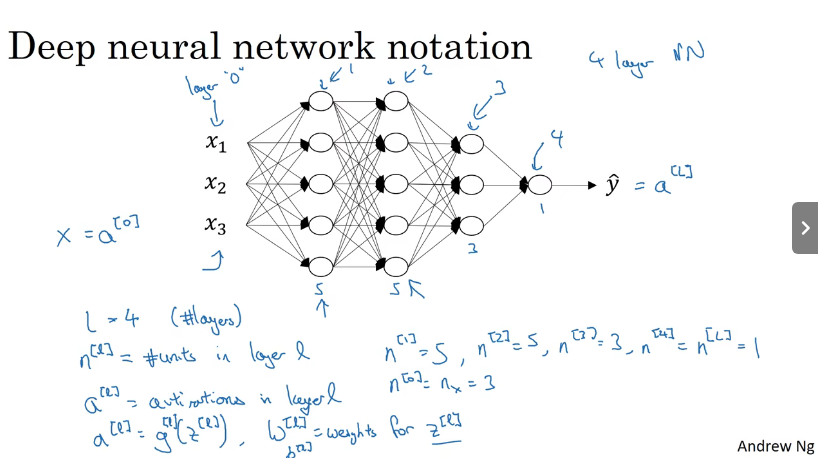
在上述例子上，l=4，n^[1]=5，n^[2]=5，n^[3]=3，n^[4]=1

深层神经网络的正向传播

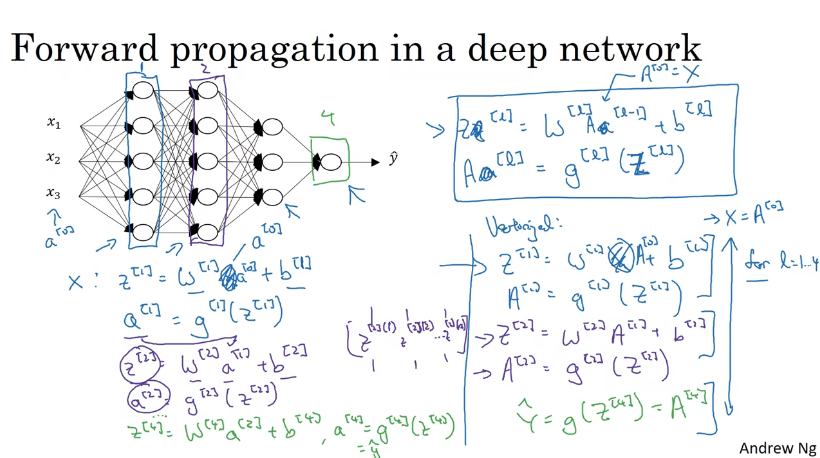
对于上面的例子，正向传播的计算如下。对于第l层的z^[l]，就是这一层的权重参数W^[l]乘上一层激活函数的输出a^[l-1]加上这层的偏置b^[l]

\[z^{[1]} = W^{[1]}a^{[0]}+b^{[1]};\quad a^{[1]}=g^{[1]}(z^{[1]})\quad --\quad Z^{[1]}=W^{[1]}A{[0]}+b^{[1]};\quad A^{[1]}=g^{[1](Z^{[1]})}\\ z^{[2]} = W^{[2]}a^{[1]}+b^{[2]};\quad a^{[2]}=g^{[2]}(z^{[2]})\quad --\quad Z^{[2]}=W^{[2]}A{[1]}+b^{[2]};\quad A^{[2]}=g^{[2](Z^{[2]})}\\ z^{[3]} = W^{[3]}a^{[2]}+b^{[3]};\quad a^{[3]}=g^{[3]}(z^{[2]})\quad --\quad Z^{[3]}=W^{[3]}A{[2]}+b^{[3]};\quad A^{[3]}=g^{[3](Z^{[3]})}\\ z^{[4]} = W^{[4]}a^{[3]}+b^{[4]};\quad a^{[4]}=g^{[2]}(z^{[4]})\quad --\quad Z^{[4]}=W^{[4]}A{[3]}+b^{[4]};\quad A^{[4]}=g^{[4](Z^{[4]})}\\ \]

由此可以归纳推导出对于第l层的正向传播公式如下。在代码中通过使用for循环，遍历layer来实现对每一层正向传播的计算。

\[z^{[l]} = W^{[l]}a^{[l-1]}+b^{[l]};\quad a^{[l]}=g^{[l]}(z^{[l]})\quad --\quad Z^{[l]}=W^{[l]}A{[l-1]}+b^{[l]};\quad A^{[l]}=g^{[l]}(Z^{[l]})\\ \]

这些步骤就是将前面浅层神经网络的步骤多重复几遍。

对矩阵维度的考虑

对于矩阵的维度，通过一个例子来推导出对于第l层的运算中z^[l]，W^[l]、a^[l-1]、b^[l]的维度大小。

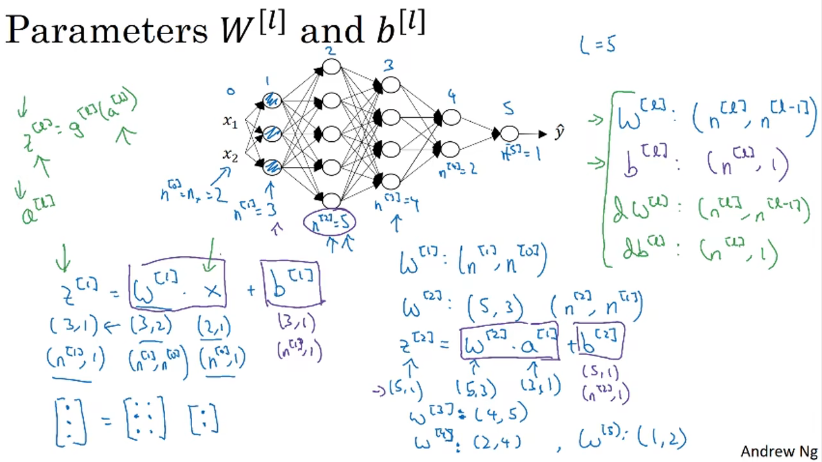
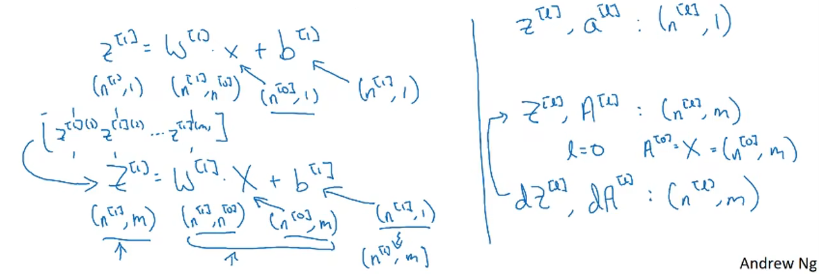
导数也和原矩阵的维度一样；在进行向量化转变以后，参数W和b的维度保持不变

\[w^{[l]}:(n^{[l]},n^{[l-1]})-dw^{[l]}:(n^{[l]},n^{[l-1]})\\ b^{[l]}:(n^{[l]},1)-db^{[l]}:(n^{[l]},1)\\ z^{[l]}:(n^{[l]},1)-Z^{[l]}:(n^{[l]},m)-dZ^{[l]}:(n^{[l]},m)\\ a^{[l]}:(n^{[l]},1)-A^{[l]}:(n^{[l]},m)-dA^{[l]}:(n^{[l]},m)\\ \]

为什么使用深层表示

在图像处理领域，深层神经网络随着层数由浅到深，神经网络提取的特征也是从边缘到局部特征到整体，由简单到复杂。如果隐藏层足够多，那么能够提取的特征就越丰富、越复杂，模型的准确率就会越高。

在语音识别领域，浅层的神经元能够检测一些简单的音调，然后较深的神经元能够检测出基本的音素，更深的神经元就能够检测出单词信息。如果网络够深，还能对短语、句子进行检测。

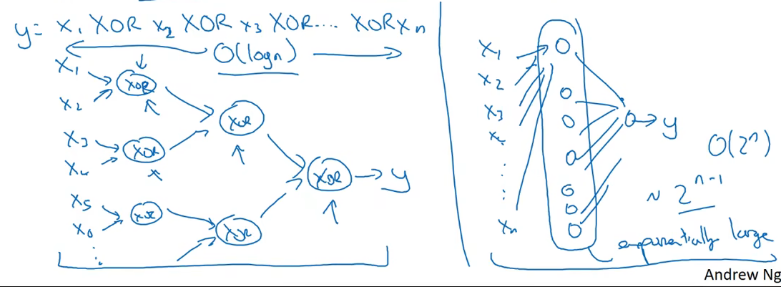
通过神经网络输入如下这样的y，通过deep layer NN，这样一个过程的神经单元的数量级是O(log_n)；而如果使用shallow layer NN，那么对应的神经单元的数量级是O(2ⁿ)。不难看出如当使用较浅层的神经网络那么需要的神经单元的数量就会很多。

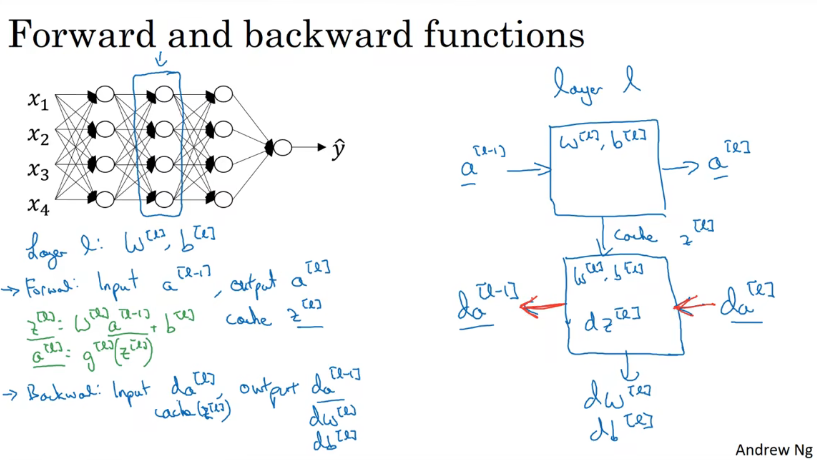
Forward and backward的公式

forward

输入：a^[l-1]

输出：a^[l]

缓存：z^[l]、W^[l]、b^[l]

\[z^{[l]} = W^{[l]}a^{[l-1]}+b^{[l]};\quad a^{[l]}=g^{[l]}(z^{[l]})\\ Z^{[l]}=W^{[l]}A{[l-1]}+b^{[l]};\quad A^{[l]}=g^{[l]}(Z^{[l]})\\ \]

backforward

输入：da^[l]

输出：da^[l-1]、dW^[l]、db^[l]

\[dz^{[l]}=da^{[l]}*g^{[l]}(z^{[l]})--dZ^{[l]}=dA^{[l]}*g^{[l]}(Z^{[l]})\\ dW^{[l]}=dz^{[l]}*a^{[l-1].T}--dW^{[l]}=\frac{1}{m}*dZ^{[l]}*A^{[l-1].T}\\ db^{[l]}=dz^{[l]}--db^{[l]}=\frac{1}{m}*np.sum(dZ^{[l]},axis=1,keepdims=True)\\ da^{[l-1]}=W^{[l].T}*dz^{[l]}--dA^{[l-1]}=W^{[l].T}*dZ^{[l]} \]

Build a deep network

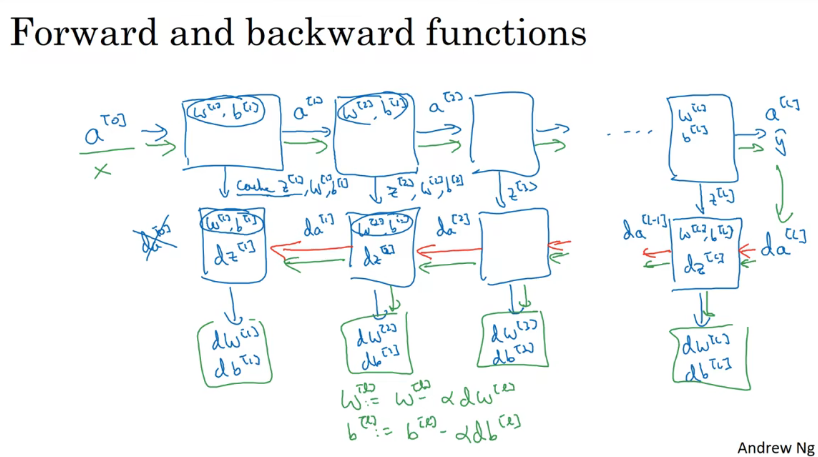
参数和超参数

参数：模型可以根据数据主动学习出的变量。比如权重参数W和偏置参数b。

超参数：超参数就是用来确定模型的参数。超参数不同，模型是不同的，那么参数也会发生相应的改变。一般通过大量的实验，根据实验结果来确定参数，也可以说是”玄学“QAQ。超参数有：学习速率\(\alpha\)、梯度下降的迭代次数、隐藏层的数量、隐藏单元的数量以及激活函数的选择等等。

对不同使用不同超参数的模型产生的结果进行评估，选择最适合的大小。

深度学习和人脑的关联性：老师说没啥大关系（not a whole lot）。balabala