图神经网络学习笔记2.1-图游走算法(同构图)
图游走类算法的目标:学习出图中每一个节点的一维表示,即node embeddings:
1.得到node embeddings之后,可以进行下游任务(节点分类等)
2.通过node embeddings可以学习节点和邻居的关系,更好的表示图结构与图特征的信息
那么,如何得到node embeddings呢?
答案是:图游走类算法,下图简单的说明了什么是图游走(图中展示的游走序列并不是全部),通过图表示学习使用图上的多次游走得到的序列,从而得到节点的一维表示(用于下游任务)
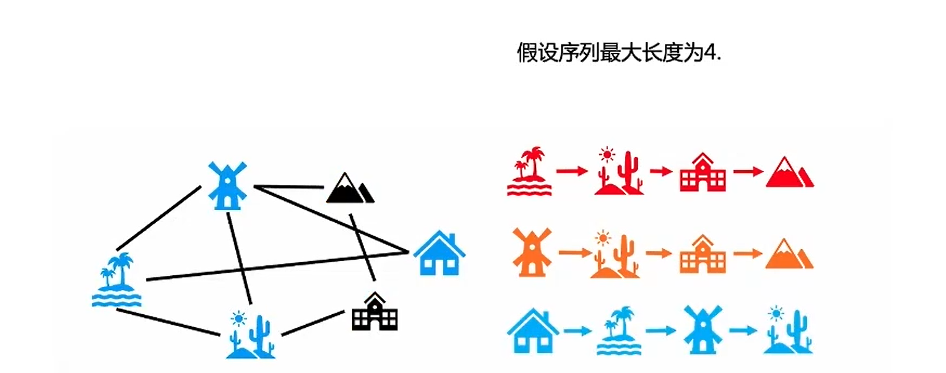
在上图中,可以将节点看作NLP中的词,将节点序列看作是NLP中的句子,下面引入NLP中的算法:word2vec。图游走类算法,最开始参考的是NLP中的word2vec模型,通过举例简单说明:
如果给出一个词语:“苹果”,它可以是水果,也可以是品牌,但在给出一些句子描述后

我们可以确定给出的“苹果”是水果而非品牌,通过这个例子可以知道词的语义是通过上下文决定的,那么word2vec是如何建立这种上下文的语义关系呢?
word2vec提出了两种训练模式:CBOW(Continuous Bag-of-Words Model)和Skip-gram (Continuous Skip-gram Model),因为图游走算法更多用到的是skip-gram,因此下面介绍skip-gram。
Sikp-gram的目的:通过中心词预测上下文,下图中的neighbors就是中心词

通过一个简单例子进行过程说明:

最后一层输出层是一个分类层,softmax:假设给定中心词orange,要预测其上下文词中的juice,计算图表中所有单词的概率,计算量很大,因此通过negative sampling(负采样)的方法进行优化

negative sampling说明:我们将样本分为正样本和负样本,如下图所示:
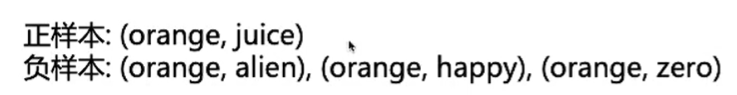
因为是二分类,因此将正样本的label标签设置为1,负样本的label标签设置为0,将softmax修改成了multiple sigmoid,sigmoid函数为二分类函数,将变量映射到0和1,数学公式如下:
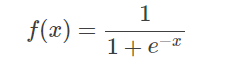
softmax层变成了多个,sigmoid层,只对正样本和选取的负样本进行分类,从而减少了计算量,通过skip-gram之后就可以得到node embeddings。
word2vec应用:图嵌入领域
通常,图中的节点会收到其邻居的影响
正式开始介绍图游走类算法:Deepwalk和node2vec(同构图游走)

在上图中,我们将NLP中的word2vec算法,应用到图嵌入领域,对于word2vec,句子是可以直接获取的,但是对于图我么,我们应该如何得到节点序列?
Deepwalk提出random walk的游走方式,如下面的例子所示,随机选取一个节点进行游走,该节点再随机选取邻居,重复以上的过程得到游走的序列,此时序列就可以类比NLP中得到的句子。
随机游走的本质:可以回头的DFS

我们可以得到下面公式:
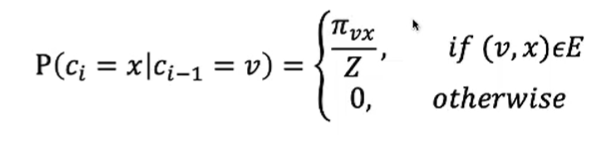
其中:
ci-1=v:当前节点
ci=x:下一个要游走的节点
pievx/Z=1/|N(v)|:N(v)表示V的邻居节点,|N(v)|表示v的邻居节点的个数。换句话说就是,等概率选择,即每一个邻居节点都有被选中的可能,且这个可能性是相同的
Deepwalk模型的整体架构:graph -> random walk + skip-gram + negative sampling,其中skip-gram -> node embeddings -> downstream task。大部分的图游走类算法都是再游走部分进行创新和改动,所以对于deepwalk算法,我们更多关注random walk这一部分。
deepwalk的缺点:它忽略了图是一个复杂的结构,而deepwalk中节点选择下一个节点的方式是均匀随机采样,且游走方式是简单直接的DFS
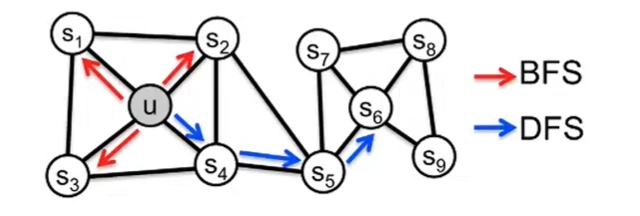
以上为图遍历的两种方法:BFS和DFS,BFS是一圈一圈散开,就像把石头扔进水面一样,而DFS是一直往前走,直到遇到死胡同再回头。
node2vec模型结合了BFS和DFS对图进行探索和学习
deepwalk是通过random walk,而node2vec则是使用bias random walk
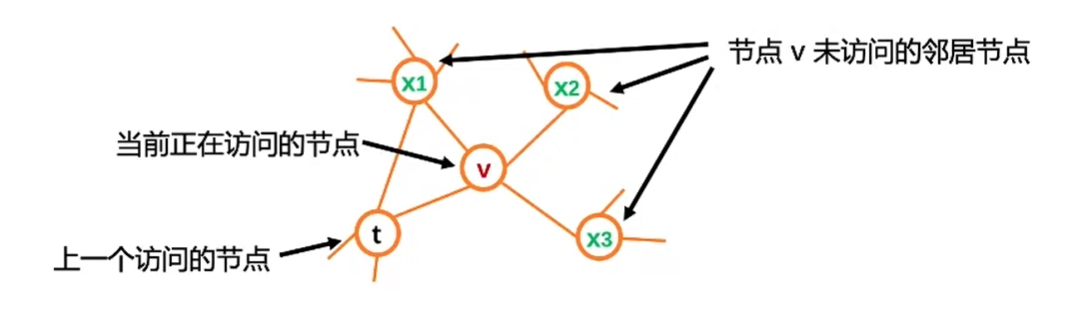
我们再次回顾deepwalk的游走方式和公式表达:
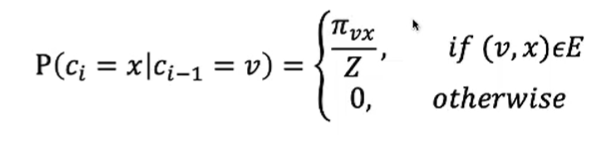
其中:
ci-1=v:当前节点
ci=x:下一个要游走的节点
pievx/Z=1/|N(v)|:N(v)表示V的邻居节点,|N(v)|表示v的邻居节点的个数。换句话说就是,等概率选择,即每一个邻居节点都有被选中的可能,且这个可能性是相同的
而node2vec中的pievx为:

可以看出,node2vec加入了边的权值,考虑了带权边,而αpq为:

其中dtx为x到t节点的距离,例如x2和x3节点需要经过v才能到达t节点,因此dtx=2,通过上述公式得到以下结果:
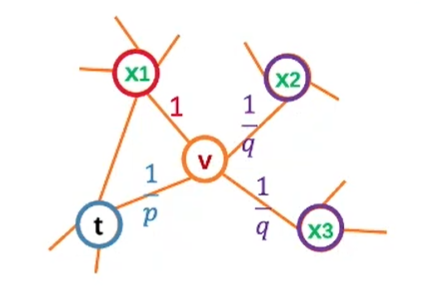
我们再继续讨论参数对于搜索的影响:
·参数p:控制随机游走以多大的概率回头
·参数q:控制随机游走偏向DFS还是BFS
q较大时(q>1),倾向于BFS
q较大时(q<1),倾向于DFS
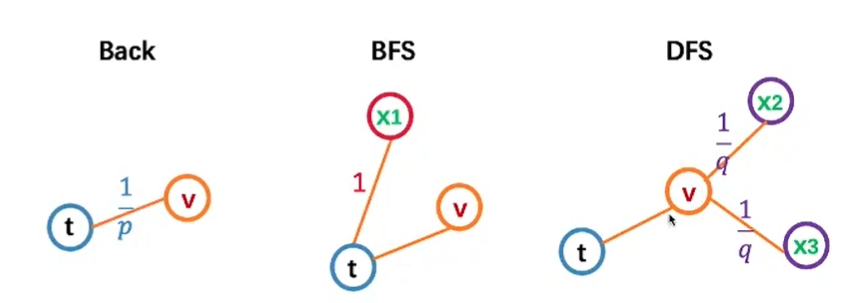
node2vec模型的整体架构:graph ->bias random walk + skip-gram + negative sampling,其中skip-gram -> node embeddings -> downstream task。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号