计算机考研之数据结构-图

数据结构-图

目录

• 数据结构-图
  • 概念
    • 定义
      • 分类
      • 属性
      • 无向图属性
      • 有向图属性
  • 存储
    • 邻接矩阵
      • 概念
      • 定义
      • 性质
    • 邻接表
      • 概念
      • 定义
      • 性质
    • 十字链表
      • 概念
      • 定义
    • 邻接多重表
      • 概念
      • 定义
  • 基本操作
  • 遍历
    • 广度优先
    • 深度优先
  • 最小生成树
    • Prim
    • kruskal
  • 最短路径
    • Dijkstra
    • Floyd
  • 拓扑排序
    • 概念
    • 算法
  • 关键路径
    • 概念
    • 算法
  • 习题

概念

定义

• 图G由点集V和边集E组成，记为G=(V,E)。
• 点集不能为空，边集可以为空。
• |V|，\(V=v_1,\cdots,v_n\)表示图点的个数，也称为图的阶。
• |E|，\(E=\{(u,v),u\in V,v\in V\}\)表示图边的个数。

有向图

• 弧是点的有序对，记做<v,u>。
• <v,u>中，v 为弧尾，w 为弧头，称点 v 到点 u 的弧，或 v 邻接到 u。

无向图

• 边是点的无序对，记做(v,u)或(u,v)。
• (v,u)中，称 v 和 u 互为邻接。

分类

简单图，图G满足：

• 不存在重复边。
• 不存在点到自身的边。

多重图，非简单图即为多重图。

属性

路径，点 u 到 点 v 的路是，u,a,b,c,d,...,v 的一个点序列。
路径长度，路径上边的个数。
回路(环)，路径中，第一个点和最后一个点相同。
简单路径，路径中，点序列不重复。
简单回路，回路中，点序列不重复。
距离，点 u 到 点 v 的最短路径。若不存在则路径为无穷大(∞)。

子图，有两个图 G=(V,E) 和 G'=(V',E')，\(V'\in V,E'\in E\) 则 G' 是 G 的子图。
生成子图，子图满足 V(G')=V(G)。

生成树，连通图中包含所有点的一个极小连通子图。

• 若图中点为 n 则其生成树有 n-1 条边。

生成森林，非连通图中所有连通分量的生成树。

带权图(网)，边上有数值的图。

无向图属性

完全图或简单完全图，无向图中，任意两个点都存在边。

• 无向完全图中，n 个点有 n(n-1)/2 条边。

连通，无向图中，点 v 到 点 u 之间有路径存在，则 v,w 是连通的。
连通图，图中任意两点都连通。
连通分量，非连通图中的极大连通子图为连通分量。

• 若一个图有 n 个点，但是只有 n-1 条边，那么必为非连通图。

点的度，与该点相连边的个数。记为TD(V)。

• 无向图全部点的度之和等于边数量的两倍，因为每条边与两个点相连。

有向图属性

有向完全图，在有向图中，任意两个点之间都存在方向相反的弧。

• 有向完全图中，n 个点 n(n-1) 条边。

强连通、强连通图、强连通分量，有向图中与无向图相对的概念。
出度，入度，出度为是以点为起点的弧的数量，记为 ID(v)。入度是以点为终点的弧的数量记为 OD(v)。TD(v)=ID(v)+OD(v)。

• 有向图全部点的出度之和与入度之和等于弧的数量。

存储

邻接矩阵

概念

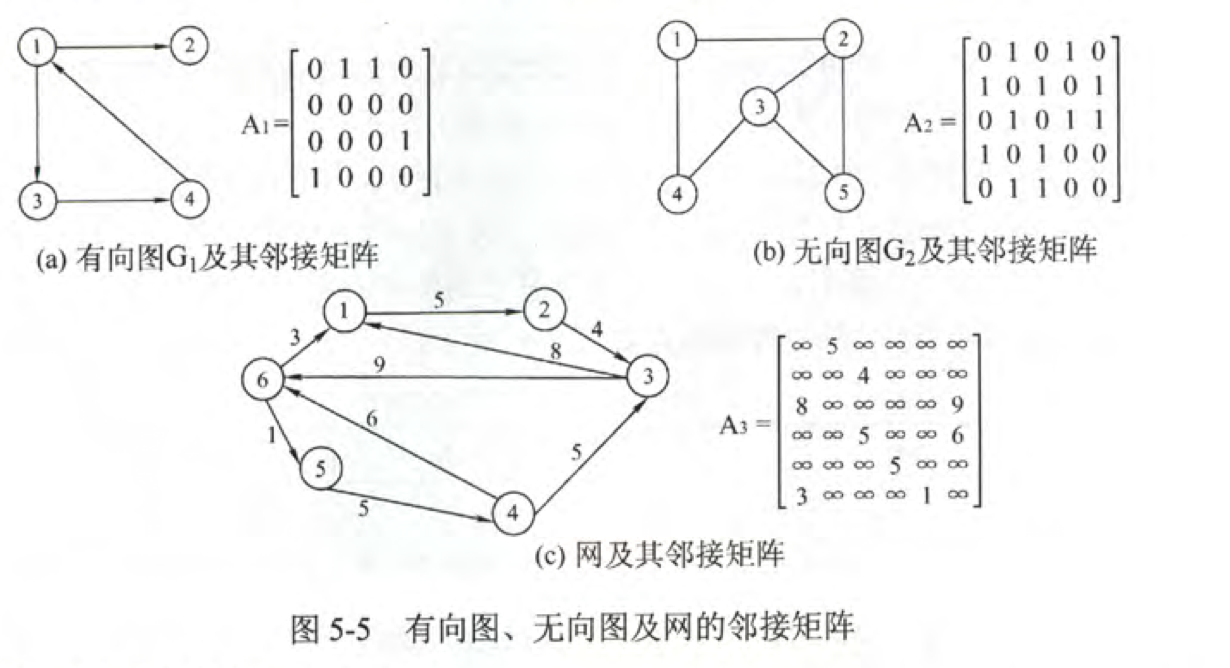
邻接矩阵即使用一个矩阵来记录点与点之间的连接信息。

对于结点数为 n 的图 G=(V,E)的邻接矩阵A 是 nxn 的矩阵。

• A[i][j]=1，若(vi,vj)或<vi,vj>或(vi,vj)是E(G)中的边。
• A[i][j]=1，若(vi,vj)或<vi,vj>或(vi,vj)不是E(G)中的边。

对带权图而言，若顶点vi，vj相连则邻接矩阵中存着该边对应的权值，若不相连则用无穷大表示。

• A[i][j]=\(w_{ij}\)，若(vi,vj)或<vi,vj>或(vi,vj)是E(G)中的边。
• A[i][j]=0或∞，若(vi,vj)或<vi,vj>或(vi,vj)不是E(G)中的边。
  

定义

# define MAXSIZE 
typedef struct {
    int vexs [MAXSIZE];
    int edges[MAXSIZE][MAXSIZE];
    int vexnum, arcnum; // 点和边的数量
}MGraph;

性质

1. 无向图的邻接矩阵为对称矩阵，可以只用上或下三角。
2. 对于无向图，邻接矩阵的第 i 行（列）非零元素的个数正好是第 i 个顶点的度 。
3. 对于有向图，邻接矩阵的第 i 行（列）非零元素的个数正好是第 i 个顶点的出度（入度）。
4. 邻接矩阵容易确定点之间是否相连，但是确定边的个数需要遍历。
5. 稠密图适合使用邻接矩阵。

邻接表

概念

对每个顶点建立一个单链表，然后所有顶点的单链表使用顺序存储。
顶点表由顶点域(data)和指向第一条邻边的指针(firstarc)构成。
边表，由邻接点域(adjvex)和指向下一条邻接边的指针域(nextarc)构成。

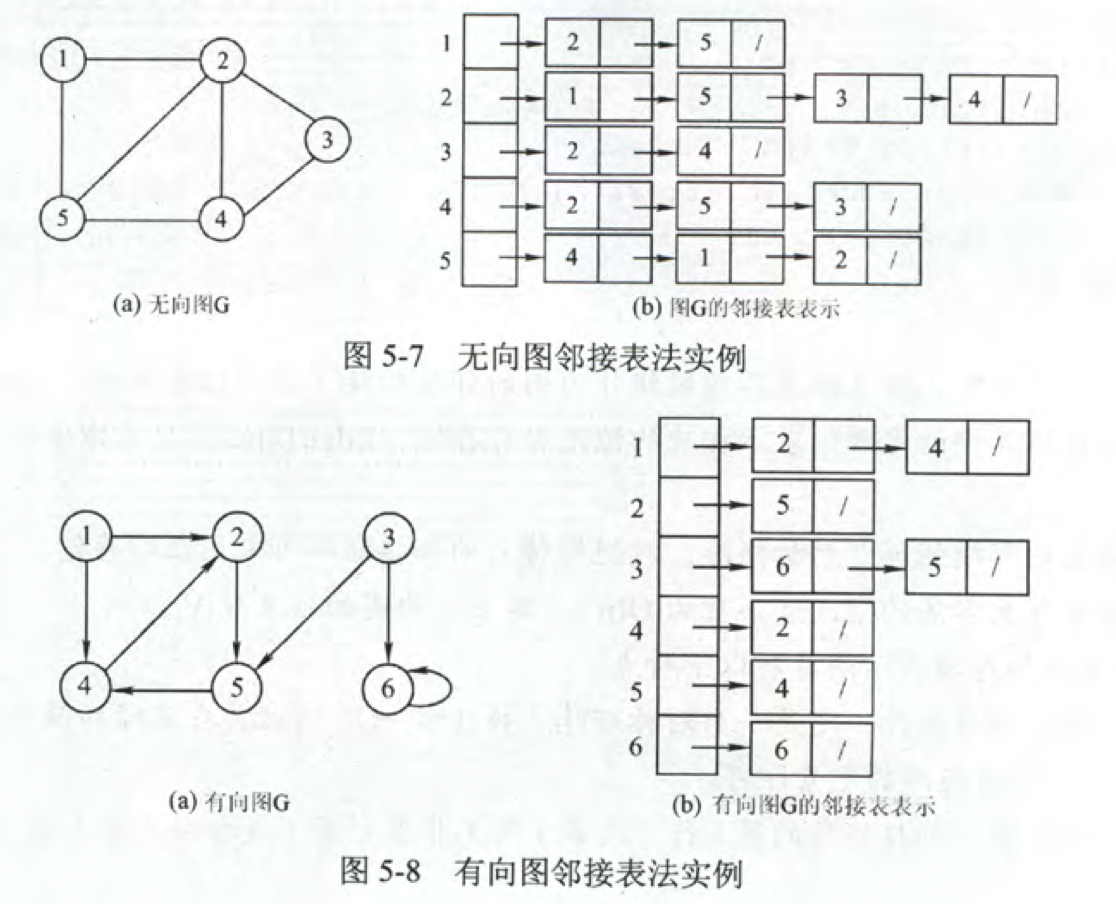
定义

typedef struct ArcNode{  // 边结点
    int adjvex; // 边指向的点
    struct ArcNode *next; //指向的下一条边
}ArcNode;

typedef struct VNnode{ //顶点节点
    int data;
    ArcNode *first;
}VNode, AdjList[MAX]

typedef struct { //邻接表
    AdjList vertices;
    int vexnum, arcnum;
} ALGraph;

性质

1. 若G为无向图，则所需的存储空间为O(|V|+2|E|)，若G为有向图，则所需的存储空间为O(|V|+|E|)。前者倍数是后者两倍是因为每条边在邻接表中出现了两次。
2. 邻接表法比较适合于稀疏图。
3. 点找边很容易，点找边不容易。
4. 邻接表的表示不唯一

十字链表

概念

有向图的一种表示方式。
十字链表中每个弧和顶点都对应有一个结点。

• 弧结点：tailvex, headvex, hlink, tlink, info
  • headvex, tailvex 分别指示头域和尾域。
  • hlink, tlink 链域指向弧头和弧尾相同的下一条弧。
  • info 指向该弧相关的信息。
• 点结点：data, firstin, firstout
  • 以该点为弧头或弧尾的第一个结点。

定义

typedef struct ArcNode{
    int tailvex, headvex;
    struct ArcNode *hlink, *tlink;
    //InfoType info;
} ArcNode;
typedef struct VNode{
    int data;
    ArcNode *firstin, *firstout;
}VNode;
typeder struct{
    VNode xlist[MAX];
    int vexnum, arcnum;
} GLGrapha;

邻接多重表

概念

邻接多重表是无向图的一种链式存储方式。

边结点：

• mark 标志域，用于标记该边是否被搜索过。
• ivex, jvex 该边的两个顶点所在位置。
• ilink 指向下一条依附点 ivex 的边。
• jlink 指向下一条依附点 jvex 的边。
• info 边相关信息的指针域。

点结点：

• data 数据域
• firstedge 指向第一条依附于改点的边。

邻接多重表中，依附于同一点的边串联在同一链表中，由于每条边都依附于两个点，所以每个点会在边中出现两次。

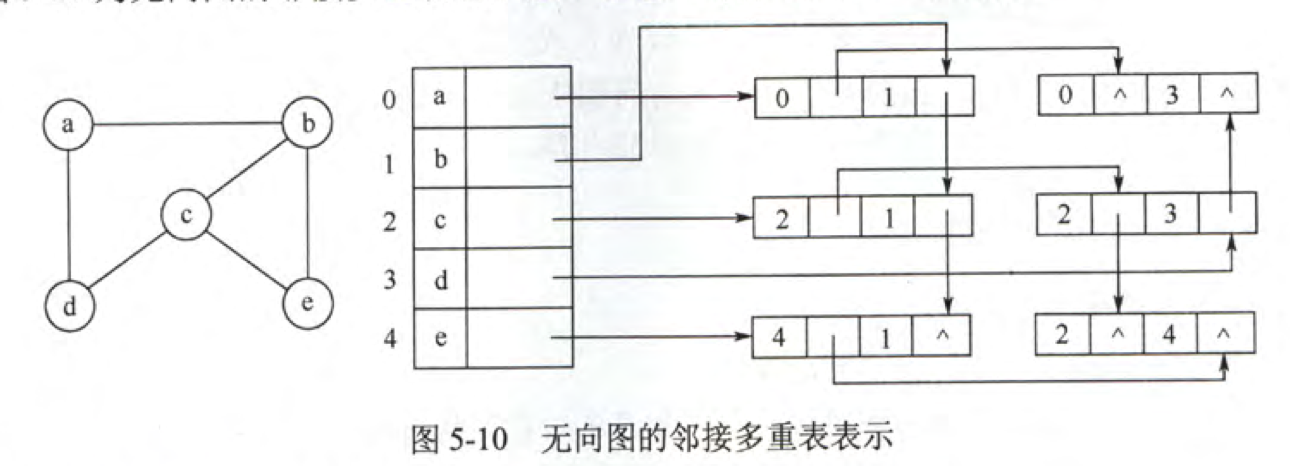
定义

typedef struct ArcNode{
    bool mark;
    int ivex, jvex;
    struct ArcNode *ilink, *jlink;
    // InfoType info;
}ArcNode;
typedef struct VNode{
    int data;
    ArcNode *firstedge;
}VNode;
typedef struct {
    VNode adjmulist[MAX];
    int vexnum, arcnum;
} AMLGraph;

基本操作

• Adjacent(G,x,y)，判断图是否存在边(x,y)或<x,y>。
• Neighbors，列出图中与 x 邻接的边。
• InsertVertex(G,x)，在图中插入顶点 x。
• DeleteVertex(G,x)，在图中删除顶点 x。
• AddEdge(G,x,y)，如果(x,y)或<x,y>不存在，则添加。
• RemoveEdge(G,x,y)，如果(x,y)或<x,y>存在，则删除。
• FirstNeighbor(G,x)，求图中顶点 x 的第一个邻接点。存在返回顶点号，不存在返回-1。
• NextNeighbor(G,x,y)，返回除x的的下一个邻接点，不存在返回-1；
• GetEdgeValue(G,x,y)，获得(x,y)或<x,y>的权值。
• SetEdgeValue(G,x,y)，设置(x,y)或<x,y>的权值。

遍历

广度优先

广度优先搜索(BFS)有点类似于二叉树的层序遍历算法。从某个顶点 v 开始遍历与 v 邻近的 w1,w2,3...，然后遍历与 w1,w2,3...wi 邻近的点。

由于 BFS 是一种分层的搜索算法，所以必须要借助一个辅助的空间。

//初始化操作
bool visited[MAX];
for(int i=0;i<G.vexnum;i++) visited[i]=FALSE;

void BFSTraverse(Graph G){
    InitQueue(Q);
    for(int i=0;i<G.vexnum;i++){
        if(!visited[i])
            BFS(G, i);
    }
}

void BFS(Graph G, int v){
    visit(v);
    visited[v]=TRUE;
    Enqueue(Q,v);
    while(!isEmpty(Q)){
        Dequeue(Q,v);
        for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w)){
            if(!visited[w]){
                visit[w];
                visited[w]=TRUE;
                EnQueue(Q,w);
            }
        }
    }
}

时间复杂度分析：
邻接表：O(|V|+|E|)
邻接矩阵:O(|V|^2)

深度优先

//初始化操作
bool visited[MAX];
for(int v=0;v<G.vexnum;v++) visited[v]=FALSE;

void DFSTraverse(Graph G){
    for(int v=0;v<G.vexnum;v++){
        if(!visited[v])
            DFS(G,v);
    }
}

void DFS(Graph G,int v){
    visit(v);
    visited[v]=TRUE;
    for(w=FistNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))
        if(!visited[w]) 
            DFS(G,w)
}

最小生成树

一个连通图的生成树是图的极小连通子图，即包含图中所有顶点，且只包含尽可能少的边的树。
对于一个带权的连通图，生成树不同，对应的权值也不同，权值最小的那棵生成树就是最小生成树。

对于最小生成树，有如下性质：

1. 最小生成树不唯一，但是对应的权值唯一。
2. 边数为顶点数减一。

构造最小生成树有多种算法，但是一般会用到以下性质：
若 G 是一个带权连通无向图，U 是 点集 V 的一个非空子集。若(u,v)其中 u∈U，v∈V-U，是一条具有最小权值的边，则必定存在一棵包含边(u,v)的最小生成树。

通用算法如下：

MST(G){
    T=NULL;
    while T未形成生成树;
        do 找到一条最小代价边(u,v)且加入 T 后不会产生回路;
            T=T∪(u,v)
}

Prim

Prim算法的执行非常类似于寻找图最短路径的Dijkstra算法。
从某个顶点出发遍历选取周围最短的边。

//伪代码描述
void Prim(G,T){
    T=∅;
    U={w}; //w为任意顶点
    while((V-U)!=∅){
        找到(u,v),u∈U,v∈(V-U),且权值最小;
        T=T∪{(u,t)};
        U=U∪{v}
    }
}

以邻接矩阵为例：

void Prim(MGraph G)
{
    int sum = 0;
    int cost[MAXSIZE];
    int vexset[MAXSIZE];
    for(int i=0;i<G.vexnum;i++) cost[i]=G.edges[0][i];
    for(int i=0;i<G.vexnum;i++) vexset[i] = FALSE;
    vexset[0]=TRUE;

    for(int i=1;i<G.vexnum;i++)
    {
        int mincost=INF;
        int minvex;
        int curvex;
        for(int j=0;j<G.vexnum;j++)
        {
            if(vexset[j]==FALSE&&cost[j]<mincost)
            {
                mincost=cost[j];
                minvex=j;
            }
            vexset[minvex]=TRUE;
            curvex = minvex;
        }
        sum+=mincost;
        for(int j=0;j<G.vexnum;j++)
            if(vexset[j]==FALSE&&G.edges[curvex][j]<cost[j])
                cost[j]=G.edges[curvex][j]
    }
}

Prim算法的复杂度为O(|V|^2)不依赖于|E|，所以适合于边稠密的图。

构造过程：

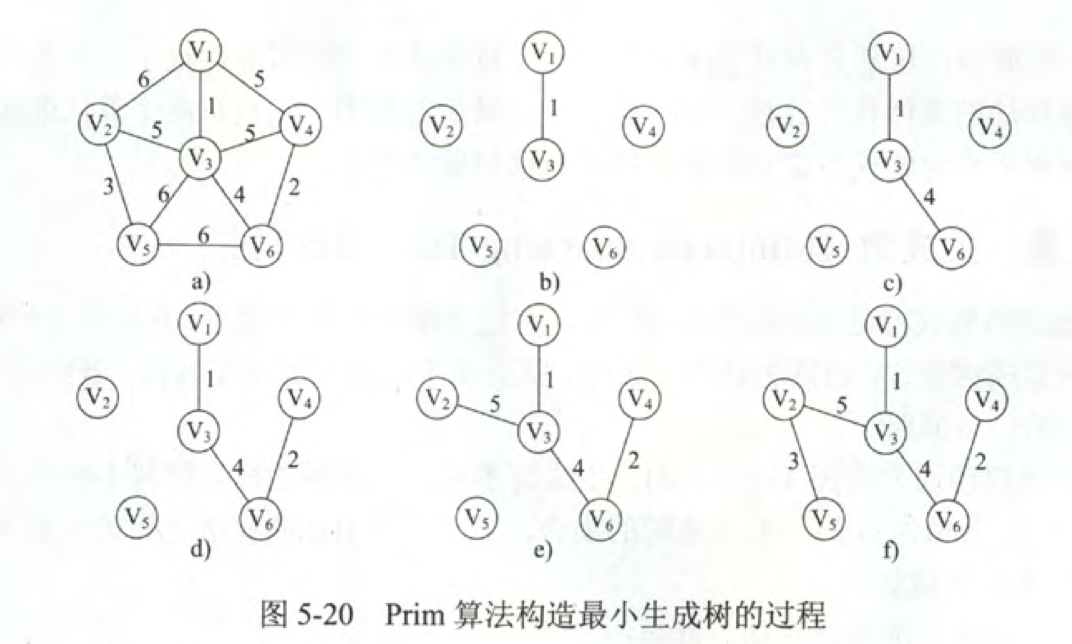
kruskal

kruskal所做的事情跟prim是反过来的，kruskal算法对边进行排序，依次选出最短的边连到顶点上。

//伪代码描述
void Kruskal(V,T){
    T=V;
    numS=n; //连通分量数
    while(nums>1){
        从E选出权值最小的边(v,u);
        if(v和u属于T中不同的连通分量){
            T=∪{(v,u)};
            nums--;
        }
    }
}

同样以邻接矩阵为例。

typedef struct
{
    int v1,v2;
    int w;
} Road;
Road road[MAXSIZE];
int v[MAXSIZE];
int getRoot(int x)
{
    while(x!=v[x]) x=v[x];
    return x;
}
void Kruskal(MGraph G, Road road[])
{
    int sum=0;
    for(int i=0;i<G.vexnum;i++) v[i]=i;
    sort(road,G.arcnum);
    for(int i=0;i<G.arcnum;i++)
    {
        int v1=getRoot(road[i].v1);
        int v2=getRoot(road[i].v2);
        if(v1!=v2)
        {
            v[v1]=v2;
            sum+=road[i].w;
        }
    }
}

kruskal算法的复杂度为O(|E|log|E|)适合边少点多的图。

构造过程：

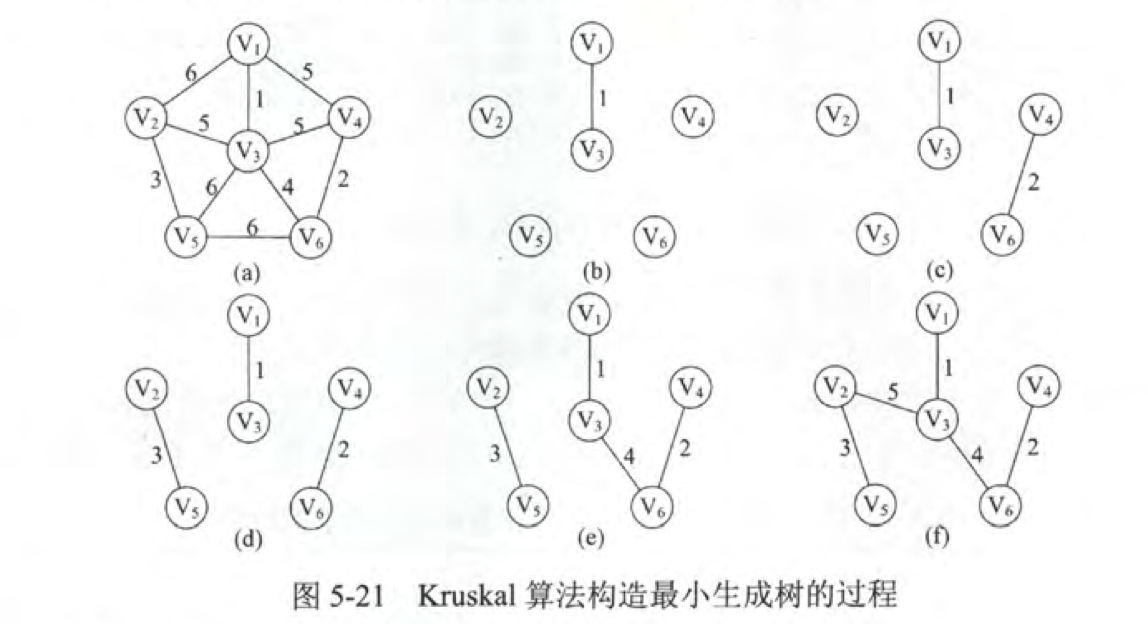
最短路径

最短路径算法一般会利用最短路径的一条性质，即：两点间的最短路径也包含了路径上其他顶点间的最短路径。

Dijkstra

Dijkstra 算法一般用于求单源最短路径问题。即一个顶点到其他顶点间的最短路径。

这里我们需要用到三个辅助数组：

• dist[vi]，从 v0 到每个顶点 vi 的最短路径长度。
• path[vi]，保存从 v0 到 vi 最短路径上的前一个顶点。
• set[]，标记点是否被并入最短路径。

执行过程：

• 初始化：
  • 选定源点 v0。
  • dist[vi]：若 v0 到 vi 之间若存在边，则为边上的权值，否则为∞。
  • path[vi]：若 v0 到 vi 之间存在边，则 path[vi]=v0，否则为-1。
  • set[v0]=TRUE，其余为 FALSE。
• 执行：
  1. 从当前的 dist[]数组中选出最小值 dist[vu]。
  2. 将 set[vu] 置为TRUE。
  3. 检测所有 set[vi]==FALSE 的点。
  4. 比较 dist[vi] 和 dist[vu]+w 的大小，w 为 <vu,vi>的权值。
  5. 如果 dist[vu]+w<dist[vi]
  6. 更新 path[] 并将 vu 加入路径中
  7. 直到遍历完所有的顶点(n-1次)

结合图来理解就是：

void Dijkstra(MGraph G, int v)
{
    int set[MAXSIZE];
    int dist[MAXSIZE];
    int path[MAXSIZE];
    int min;
    int curvex;
    for(int i=0;i<G.vexnum;i++)
    {
        dist[i]=G.edges[v][i];
        set[i]=FALSE;
        if(G.edges[v][i]<INF) path[i]=v;
        else path[i]=-1;
    }
    set[v]=TRUE;path[v]=-1;
    
    for(int i=0;i<G.vexnum-1;i++)
    {
        min=INF;
        for(int j=0;j<G.vexnum;j++)
        {
            if(set[j]==FALSE;&&dist[j]<min)
            {
                curvex=j;
                min=dist[j];
            }
            set[curvex]=TRUE;
        }
        for(int j=0;j<G.vexnum;j++)
        {
            if(set[j]==FALSE&&(dist[curvex]+G.edges[curvex][j])<dist[j])
            {
                dist[j]=dist[u]+G.edges[curvex][j];
                path[j]=curvex;
            }
        }
    }
}

复杂度分析：从代码可以很容易看出来这里有两层的for循环，时间复杂度为O(n^2)。
适用性：不适用于带有负权值的图。

Floyd

floyd算法是求图中任意两个顶点间的最短距离。

过程：

• 初始化一个矩阵A，\(A^{(-1)}\)[i][j]=G.edges[i][j]。
• 迭代n轮：\(A^{(k)}\)=Min{\(A^{(k-1)}\)[i][j], \(A^{(k-1)}\)[i][k]+\(A^{(k-1)}\)[k][j]}

\(A^{(k)}\)矩阵存储了前K个节点之间的最短路径，基于最短路径的性质，第K轮迭代的时候会求出第K个节点到其他K-1个节点的最短路径。

图解：

void Floyd(MGraph G, int Path[][MAXSIZE])
{
    int A[MAXSIZE][MAXSIZE];
    for(int i=0;i<G.vexnum;i++)
        for(int j=0;j<G.vexnum;j++)
        {
            A[i][j]=G.edges[i][j];
            Path[i][j]=-1;
        }

    for(int k=0;k<G.vexnum;k++)
        for(int i=0;i<G.vexnum;i++)
            for(int j=0;j<G.vexnum;j++)
                if(A[i][j]>A[i][k]+A[k][j])
                {
                    A[i][j]=A[i][k]+A[k][j];
                    Path[i][j]=k;
                }
}

复杂度分析：主循环为三个for，O(n^3)。
适用性分析：允许图带有负权边，但是不能有负权边构成的回路。

拓扑排序

概念

• DAG，有向无环图。
• AOV网，用<Vi,Vj>表示 Vi 先于 Vj 的关系构成的DAG。即每个点表示一种活动，活动有先后顺序。
• 拓扑排序，满足以下关系的DAG，即求AOV网中可能的活动顺序：
  • 每个顶点只出现一次。
  • 若顶点 A 在顶点 B 之前，则不存在 B 到 A 的路径。

算法

一种比较常用的拓扑排序算法：

1. 从DAG图中选出一个没有前驱的顶点删除。
2. 从图中删除所有以该点为起点的边。
3. 重复1,2。直到图为空。若不为空则必有环。

最终得到的拓扑排序结果为：1,2,4,3,5。

关键路径

概念

在带权有向图中，若权值表示活动开销则为AOE网。
AOE网的性质：

1. 只有顶点的的事件发生后，后继的顶点的事件才能发生。
2. 只有顶点的所有前驱事件发生完后，才能进行该顶点的事件。

源点：AOE 中仅有一个入度为0的顶点。
汇点：AOE 中仅有一个出度为0的顶点。

关键路径：从源点到汇点的所有路径中路径长度最大的。
关键路径长度：完成整个工程的最短时间。
关键活动：关键路径上的活动。

算法

先定义几个量：

1. ve(k)，事件 vk 最早发生时间。决定了所有从 vj 开始的活动能开工的最早时间。
   • ve(源点)=0。
   • ve(k)=Max{ve(j)+Weight(vj,vk)}。
   • 注意从前往后算。
2. vl(k)，事件 vk 最迟发生的时间。保证所指向的事件 vi 能在 ve(i)之前完成。
   • vl(汇点)=ve(汇点)。
   • vl(k)=Min{vl(k)-Weight(vj,vk)}。
   • 注意从后往前算。
3. e(i)，活动 ai 最早开始的时间。
   • 若边<vk,vj>表示活动 ai，则有 e(i)=ve(k)。
4. l(i)，活动 ai 最迟开始时间。
   • l(i)=vl(i)-Weight(vk, vj)。
5. d(i)，活动完成的时间余量。
   • d(i)=l(i)-e(i)。
   • l(i)=e(i)则为关键活动。

求关键路径算法如下：

1. 求 AOE 网中所有事件的 ve()
2. 求 AOE 网中所有事件的 vl()
3. 求 AOE 网中所有活动的 e()
4. 求 AOE 网中所有活动的 l()
5. 求 AOE 网中所有活动的 d()
6. 所有 d()=0的活动构成关键路径

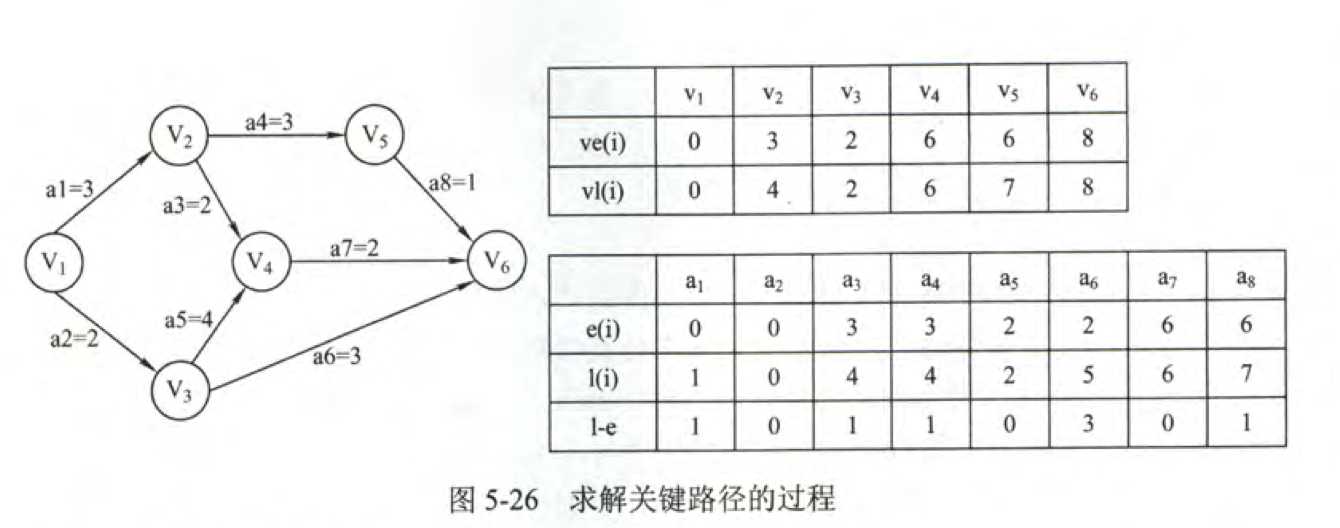
可以求得关键路径为(v1,v3,v4,v6)

习题