深度学习-无监督
原:http://www.cnblogs.com/DjangoBlog/p/6476332.html
综述
如果已经有一个足够强大的机器学习算法,为了获得更好的性能,最靠谱的方法之一是给这个算法以更多的数据。机器学习界甚至有个说法:“有时候胜出者并非有最好的算法,而是有更多的数据。”
人们总是可以尝试获取更多的已标注数据,但是这样做成本往往很高。例如研究人员已经花了相当的精力在使用类似 AMT(Amazon Mechanical Turk) 这样的工具上,以期获取更大的训练数据集。相比大量研究人员通过手工方式构建特征,用众包的方式让多人手工标数据是一个进步,但是我们可以做得更好。具体的说,如果算法能够从未标注数据中学习,那么我们就可以轻易地获取大量无标注数据,并从中学习。自学习和无监督特征学习就是这种的算法。尽管一个单一的未标注样本蕴含的信息比一个已标注的样本要少,但是如果能获取大量无标注数据(比如从互联网上下载随机的、无标注的图像、音频剪辑或者是文本),并且算法能够有效的利用它们,那么相比大规模的手工构建特征和标数据,算法将会取得更好的性能。
在自学习和无监督特征学习问题上,可以给算法以大量的未标注数据,学习出较好的特征描述。在尝试解决一个具体的分类问题时,可以基于这些学习出的特征描述和任意的(可能比较少的)已标注数据,使用有监督学习方法完成分类。
在一些拥有大量未标注数据和少量的已标注数据的场景中,上述思想可能是最有效的。即使在只有已标注数据的情况下(这时我们通常忽略训练数据的类标号进行特征学习),以上想法也能得到很好的结果。
特征学习
我们已经了解到如何使用一个自编码器(autoencoder)从无标注数据中学习特征。具体来说,假定有一个无标注的训练数据集 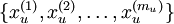 (下标
(下标 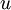 代表“不带类标”)。现在用它们训练一个稀疏自编码器(可能需要首先对这些数据做白化或其它适当的预处理)。
代表“不带类标”)。现在用它们训练一个稀疏自编码器(可能需要首先对这些数据做白化或其它适当的预处理)。
利用训练得到的模型参数 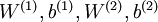 ,给定任意的输入数据
,给定任意的输入数据  ,可以计算隐藏单元的激活量(activations)
,可以计算隐藏单元的激活量(activations) 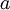 。如前所述,相比原始输入
。如前所述,相比原始输入  来说,
来说,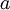 可能是一个更好的特征描述。下图的神经网络描述了特征(激活量
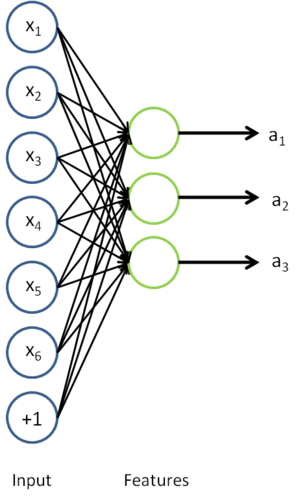
可能是一个更好的特征描述。下图的神经网络描述了特征(激活量 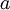 )的计算。
)的计算。
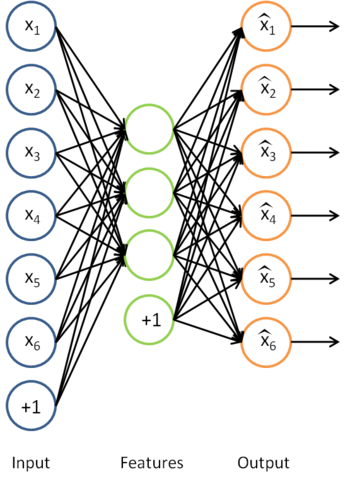
这实际上就是之前得到的稀疏自编码器,在这里去掉了最后一层。
假定有大小为 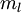 的已标注训练集
的已标注训练集 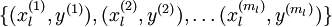 (下标
(下标  表示“带类标”),我们可以为输入数据找到更好的特征描述。例如,可以将
表示“带类标”),我们可以为输入数据找到更好的特征描述。例如,可以将 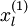 输入到稀疏自编码器,得到隐藏单元激活量
输入到稀疏自编码器,得到隐藏单元激活量 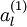 。接下来,可以直接使用
。接下来,可以直接使用 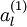 来代替原始数据
来代替原始数据 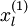 (“替代表示”,Replacement Representation)。也可以合二为一,使用新的向量
(“替代表示”,Replacement Representation)。也可以合二为一,使用新的向量 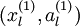 来代替原始数据
来代替原始数据 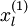 (“级联表示”,Concatenation Representation)。
(“级联表示”,Concatenation Representation)。
经过变换后,训练集就变成 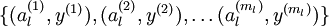 或者是
或者是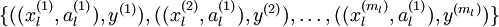 (取决于使用
(取决于使用 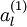 替换
替换 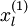 还是将二者合并)。在实践中,将
还是将二者合并)。在实践中,将 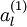 和
和 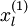 合并通常表现的更好。但是考虑到内存和计算的成本,也可以使用替换操作。
合并通常表现的更好。但是考虑到内存和计算的成本,也可以使用替换操作。
最终,可以训练出一个有监督学习算法(例如 svm, logistic regression 等),得到一个判别函数对 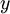 值进行预测。预测过程如下:给定一个测试样本
值进行预测。预测过程如下:给定一个测试样本 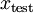 ,重复之前的过程,将其送入稀疏自编码器,得到
,重复之前的过程,将其送入稀疏自编码器,得到 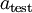 。然后将
。然后将 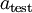 (或者
(或者 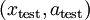 )送入分类器中,得到预测值。
)送入分类器中,得到预测值。
数据预处理
在特征学习阶段,我们从未标注训练集 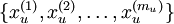 中学习,这一过程中可能计算了各种数据预处理参数。例如计算数据均值并且对数据做均值标准化(mean normalization);或者对原始数据做主成分分析(PCA),然后将原始数据表示为
中学习,这一过程中可能计算了各种数据预处理参数。例如计算数据均值并且对数据做均值标准化(mean normalization);或者对原始数据做主成分分析(PCA),然后将原始数据表示为 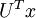 (又或者使用 PCA 白化或 ZCA 白化)。这样的话,有必要将这些参数保存起来,并且在后面的训练和测试阶段使用同样的参数,以保证数据进入稀疏自编码神经网络之前经过了同样的变换。例如,如果对未标注数据集进行PCA预处理,就必须将得到的矩阵
(又或者使用 PCA 白化或 ZCA 白化)。这样的话,有必要将这些参数保存起来,并且在后面的训练和测试阶段使用同样的参数,以保证数据进入稀疏自编码神经网络之前经过了同样的变换。例如,如果对未标注数据集进行PCA预处理,就必须将得到的矩阵 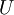 保存起来,并且应用到有标注训练集和测试集上;而不能使用有标注训练集重新估计出一个不同的矩阵
保存起来,并且应用到有标注训练集和测试集上;而不能使用有标注训练集重新估计出一个不同的矩阵 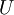 (也不能重新计算均值并做均值标准化),否则的话可能得到一个完全不一致的数据预处理操作,导致进入自编码器的数据分布迥异于训练自编码器时的数据分布。
(也不能重新计算均值并做均值标准化),否则的话可能得到一个完全不一致的数据预处理操作,导致进入自编码器的数据分布迥异于训练自编码器时的数据分布。
无监督特征学习的术语
有两种常见的无监督特征学习方式,区别在于你有什么样的未标注数据。自学习(self-taught learning) 是其中更为一般的、更强大的学习方式,它不要求未标注数据 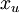 和已标注数据
和已标注数据 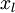 来自同样的分布。另外一种带限制性的方式也被称为半监督学习,它要求
来自同样的分布。另外一种带限制性的方式也被称为半监督学习,它要求 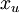 和
和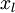 服从同样的分布。下面通过例子解释二者的区别。
服从同样的分布。下面通过例子解释二者的区别。
假定有一个计算机视觉方面的任务,目标是区分汽车和摩托车图像;也即训练样本里面要么是汽车的图像,要么是摩托车的图像。哪里可以获取大量的未标注数据呢?最简单的方式可能是从互联网上下载一些随机的图像数据集,在这些数据上训练出一个稀疏自编码器,从中得到有用的特征。这个例子里,未标注数据完全来自于一个和已标注数据不同的分布(未标注数据集中,或许其中一些图像包含汽车或者摩托车,但是不是所有的图像都如此)。这种情形被称为自学习。
相反,如果有大量的未标注图像数据,要么是汽车图像,要么是摩托车图像,仅仅是缺失了类标号(没有标注每张图片到底是汽车还是摩托车)。也可以用这些未标注数据来学习特征。这种方式,即要求未标注样本和带标注样本服从相同的分布,有时候被称为半监督学习。在实践中,常常无法找到满足这种要求的未标注数据(到哪里找到一个每张图像不是汽车就是摩托车,只是丢失了类标号的图像数据库?)因此,自学习在无标注数据集的特征学习中应用更广。
中英文对照
- 自我学习/自学习 self-taught learning
- 无监督特征学习 unsupervised feature learning
- 自编码器 autoencoder
- 白化 whitening
- 激活量 activation
- 稀疏自编码器 sparse autoencoder
- 半监督学习 semi-supervised learning
中文译者
张灵(lingzhang001@outlook.com),晓风(xiaofeng.zhb@alibaba-inc.com),王文中(wangwenzhong@ymail.com)
从自我学习到深层网络
在前一节中,我们利用自编码器来学习输入至 softmax 或 logistic 回归分类器的特征。这些特征仅利用未标注数据学习获得。在本节中,我们描述如何利用已标注数据进行微调,从而进一步优化这些特征。如果有大量已标注数据,通过微调就可以显著提升分类器的性能。
在自我学习中,我们首先利用未标注数据训练一个稀疏自编码器。随后,给定一个新样本  ,我们通过隐含层提取出特征
,我们通过隐含层提取出特征 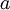 。上述过程图示如下:
。上述过程图示如下:
我们感兴趣的是分类问题,目标是预测样本的类别标号 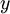 。我们拥有标注数据集
。我们拥有标注数据集 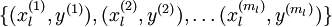 ,包含
,包含 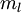 个标注样本。此前我们已经说明,可以利用稀疏自编码器获得的特征
个标注样本。此前我们已经说明,可以利用稀疏自编码器获得的特征 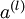 来替代原始特征。这样就可获得训练数据集
来替代原始特征。这样就可获得训练数据集 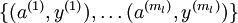 。最终,我们训练出一个从特征
。最终,我们训练出一个从特征 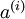 到类标号
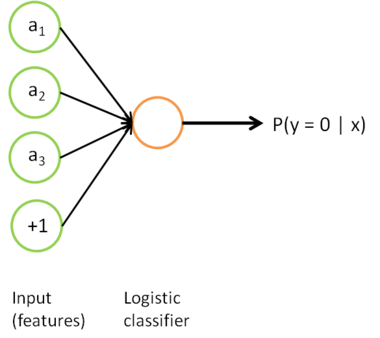
到类标号 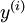 的 logistic 分类器。为说明这一过程,我们按照神经网络一节中的方式,用下图描述 logistic 回归单元(橘黄色)。
的 logistic 分类器。为说明这一过程,我们按照神经网络一节中的方式,用下图描述 logistic 回归单元(橘黄色)。
考虑利用这个方法所学到的分类器(输入-输出映射)。它描述了一个把测试样本  映射到预测值
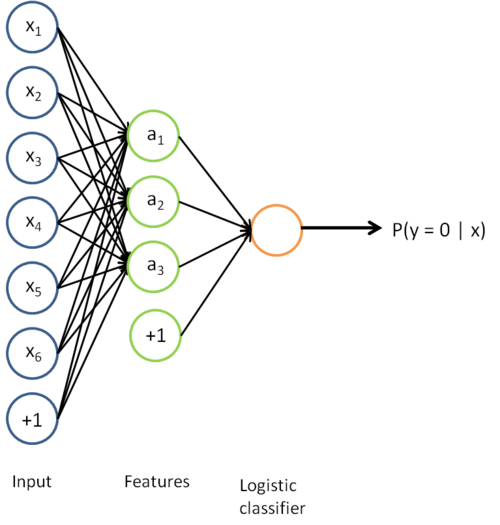
映射到预测值 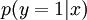 的函数。将此前的两张图片结合起来,就得到该函数的图形表示。也即,最终的分类器可以表示为:
的函数。将此前的两张图片结合起来,就得到该函数的图形表示。也即,最终的分类器可以表示为:
该模型的参数通过两个步骤训练获得:在该网络的第一层,将输入  映射至隐藏单元激活量
映射至隐藏单元激活量 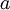 的权值
的权值 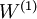 可以通过稀疏自编码器训练过程获得。在第二层,将隐藏单元
可以通过稀疏自编码器训练过程获得。在第二层,将隐藏单元 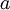 映射至输出
映射至输出 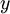 的权值
的权值 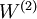 可以通过 logistic 回归或 softmax 回归训练获得。
可以通过 logistic 回归或 softmax 回归训练获得。
这个最终分类器整体上显然是一个大的神经网络。因此,在训练获得模型最初参数(利用自动编码器训练第一层,利用 logistic/softmax 回归训练第二层)之后,我们可以进一步修正模型参数,进而降低训练误差。具体来说,我们可以对参数进行微调,在现有参数的基础上采用梯度下降或者 L-BFGS 来降低已标注样本集 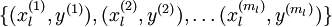 上的训练误差。
上的训练误差。
使用微调时,初始的非监督特征学习步骤(也就是自动编码器和logistic分类器训练)有时候被称为预训练。微调的作用在于,已标注数据集也可以用来修正权值 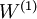 ,这样可以对隐藏单元所提取的特征
,这样可以对隐藏单元所提取的特征 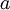 做进一步调整。
做进一步调整。
到现在为止,我们描述上述过程时,都假设采用了“替代 (Replacement)”表示而不是“级联 (Concatenation)”表示。在替代表示中,logistic 分类器所看到的训练样本格式为 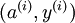 ;而在级联表示中,分类器所看到的训练样本格式为
;而在级联表示中,分类器所看到的训练样本格式为 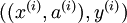 。对级联表示同样可以进行微调(在级联表示神经网络中,输入值
。对级联表示同样可以进行微调(在级联表示神经网络中,输入值 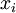 也直接被输入至 logistic 分类器。对此前的神经网络示意图稍加更改,即可获得其示意图。具体的说,第一层的输入节点除了与隐层联接之外,还将越过隐层,与第三层输出节点直接相连)。但是对于微调来说,级联表示相对于替代表示几乎没有优势。因此,如果需要开展微调,我们通常使用替代表示的网络(但是如果不开展微调,级联表示的效果有时候会好得多)。
也直接被输入至 logistic 分类器。对此前的神经网络示意图稍加更改,即可获得其示意图。具体的说,第一层的输入节点除了与隐层联接之外,还将越过隐层,与第三层输出节点直接相连)。但是对于微调来说,级联表示相对于替代表示几乎没有优势。因此,如果需要开展微调,我们通常使用替代表示的网络(但是如果不开展微调,级联表示的效果有时候会好得多)。
在什么时候应用微调?通常仅在有大量已标注训练数据的情况下使用。在这样的情况下,微调能显著提升分类器性能。然而,如果有大量未标注数据集(用于非监督特征学习/预训练),却只有相对较少的已标注训练集,微调的作用非常有限。
中英文对照
- 自我学习 self-taught learning
- 深层网络 deep networks
- 微调 fine-tune
- 稀疏自编码器 sparse autoencoder
- 梯度下降 gradient descent
- 非监督特征学习 unsupervised feature learning
- 预训练 pre-training