AUC及其计算

概念

AUC（Area Under Curve）被定义为ROC曲线下与坐标轴围成的面积，显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围在0.5和1之间。AUC越接近1.0，检测方法真实性越高;等于0.5时，则真实性最低，无应用价值.
AUC:（ROC曲线下方的面积大小）
参考：百度百科

含义理解二 ： AUC（are under curve)是一个模型的评价指标，用于分类任务。
那么这个指标代表什么呢？这个指标想表达的含义，简单来说其实就是随机抽出一对样本（一个正样本，一个负样本），然后用训练得到的分类器来对这两个样本进行预测，预测得到正样本的概率大于负样本概率的概率。
参考

AUC的计算方法

1. 方法一 ： 定义计算 -> 计算面积 -> 不好实现

2. 方法二： 从概率的角度进行实现
   有如下公式：
   

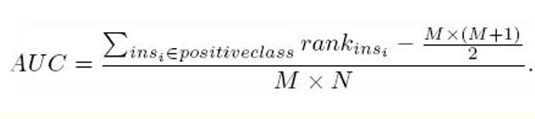
公式解释：
首先对score从大到小排序，然后令最大score对应的sample 的rank为n，第二大score对应sample的rank为n-1，以此类推。然后把所有的正类样本的rank相加，再减去M-1种两个正样本组合的情况。得到的就是所有的样本中有多少对正类样本的score大于负类样本的score。然后再除以M×N

代码实现：

import numpy as np

def calculate_auc(y, p):
    '''
    y: 真实Label的向量 ndarray
    p: 预测为正例的概率的向量 ndarray
    '''
    # 保证相同概率的0排在1前面
    tmp = np.array(sorted(zip(y, p), key=lambda x:(x[1], -x[0]), reverse=True))
    neg = 0
    pos = 0
    for i in y:
        if i == 0:
            neg += 1
        elif i == 1:
            pos += 1
    loss = 0
    neglst = np.array([])
    for i in range(len(tmp)):
        if tmp[i][0] == 1:
            loss += np.sum(neglst == tmp[i][1]) / 2 + np.sum(neglst != tmp[i][1])
        else:
            neglst = np.append(neglst, tmp[i][1])
            
    return 1 - loss / (neg*pos)

参考：
https://blog.csdn.net/lieyingkub99/article/details/81266664

https://blog.csdn.net/renzhentinghai/article/details/81095857

https://blog.csdn.net/jose_M/article/details/105587339?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.pc_relevant_is_cache&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.pc_relevant_is_cache

时间匆匆，简单记录~