二叉树中两个节点的最近公共祖先

一、递归版本

思想：假设根结点为root，其中给定的两个结点分别为A和B，它们分别都不为null。如果当前结点p为null，那么直接返回null，如果当前结点p是给定的结点中的其中一个结点，那么直接返回当前结点p(如果p是根结点，程序一次就返回了，下面的递归也不会出现)。如果当前节点不是A和B中的一个，那么需要分别去查找p的左右子树，看看是否包含A或者B，查询左右子树后，如果查询左子树和查询右子树的结果都不为null，说明当前结点p就是最近的公共祖先。否则，如果查询左子树结果为null，那么返回查询右子树的结果。反之，返回查询左子树的结果。

public static TreeNode getParent(TreeNode root, TreeNode node1,TreeNode node2) {
        if(root == null || node1 == null ||  node2 == null) return null;
        //这里可以换成if(root == node1 || root == node2),我只是为了方便测试才这样写
        if(root.val == node1.val || root.val == node2.val) return root;
        TreeNode left = getParent(root.left,node1,node2);
        TreeNode right = getParent(root.right,node1,node2);
        //如果左右子树都能找到，那么当前节点就是最近的公共祖先节点
        if(left != null && right != null) return root;
        //如果左子树上没有，那么返回右子树的查找结果
        if(left == null) return right;
        //否则返回左子树的查找结果
        else return left;
    }

二、非递归版本

思想：这里提供一种思路，代码就不演示了。因为这个思想的实现代码和查找从根到某个结点的路径的思想一样。首先，我们找出一条从根到A的路径保存到栈或者数组，相同的方式找到一条从根到B的路径也保存到栈或者数组(参考我的另一篇博客：查找从根到某结点的路径)。然后开始遍历这两个数组，找到第一次下标相同但是值不同的那么数的下标，这个下标的前一个数就是最近公共祖先。我举个例子：

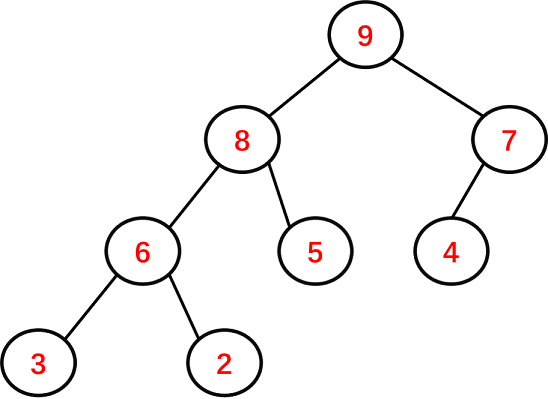
假设A为结点3，B为结点4，那么从根到A的路径为9---8---6---3，从根到B的路径为9---7---4，遍历这个两个数组，发现9 == 9，而8 ！= 7，所以9就是最近公共祖先。