如何从复杂度角度保证加密算法安全性？
Basing Cryptography on Intractable Computation
read The Joy of Cryptography
如何定义一个安全的加密算法？
我们经常讨论如何进行加密，如何设计算法来从理论上保证“不可破解”。但是从实践上来说，假如对方能够以无限的算力来猜测，那么他最终都会猜到正确的答案。
因此现代的一切加密方案几乎都是基于不存在无限（或接近无限）算力的假设，来为暴力破解之路制造困难。我们经常要量化地描述这种困难程度，因此引入一个\(\lambda\)作为Security Parameter来描述。对于一个问题，如果猜测者需要猜测\(2^\lambda\)次才能得到正确答案，那么就可以拿\(\lambda\)来描述这个问题的求解难度。
但是显然，即使我们能够量化地定义求解的难度，但是我们依然没有划清界限：我们应该设计一个多难的问题才能被视作”不可破解“的呢？答案是：当问题求解的计算复杂性随着加密对象的长度增长而指数增长时，我们可以认为该问题是”不可破解“的。同时我们也应该注意到，在这种情形下保持复杂度的指数增长是理论上能够达到的最大的增长能力。
对于一个数值型的加密对象，比如一个数字\(N\)，需要注意其在传统二进制计算机中的所谓长度是\(log_2^N\)，而在量子计算机中不一定，这也导致有时同一个加密问题在量子计算机中更容易被破解
而在求解的时间复杂度之外，我们也应该考虑到或许存在一个究极幸运儿能够在有限次的猜测中正中目标。通常来说，猜测成功的概率和求解的时间复杂度之间存在单纯的反比关系，因此我们可以将极高的时间复杂度与极低的猜测成功概率划等号。因此，我们也能类似地定义猜测成功率也应该时呈现指数趋近于零的，进一步可以表示为概率\(f(\lambda)\)可忽略，当且仅当\(f(\lambda)p(\lambda)\)随\(\lambda\)增大而趋近于0对任何一个多项式\(p(\lambda)\)成立。
指数级别的求解难度足以保证加密的安全性吗？
回到我们对安全性的定义（即我们应该无法通过函数的输出情况来分辨不同的函数），我们可以进一步放宽我们的限制：
-
函数被请求的次数仅在多项式范围内
-
两个函数的响应之间的差异只要不超过我们对”可忽略“的定义即可
这两点其实本质差不多
考虑A和B两个函数，A随机生成一个n位二进制字符串，并返回布尔值描述其是否与输入值是否相同，B则永远返回false。因为我们只能请求\(n\)的多项式可描述的次数，而实质的差异是指数级别的，这使得我们发现不了这两个函数有什么区别。从另一个更加直观的方面来说，我们发现A和B输出有差异的概率特别小，以至于我们不大可能在多项式级别的尝试中发现，因此该概率可忽略
对于多项式级别的次数q，我们可以证明以下不等式，揭示了两个程序可区分概率的上限定义
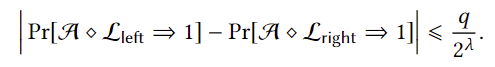
同时，既然我们讨论的是现实场景下的问题，那么就要考虑如果出现特殊情况（比如存储关键变量的电位突然翻转）时，会如何影响上述的可区分概率。假设系统关键变量bad会在出现突发情况时翻转以至于使得函数输出改变，我们可以证明以下不等式，揭示了可区分概率绝不会大于系统出问题的概率，这足以保证安全性。
不重复的猜测会对加密算法安全性产生什么影响？
上文中我们在讨论猜测行为时，认为猜测者是在可行空间内多次放回取样，那如果不放回取样呢？既然不放回取样使得猜测序列没有重复项，那么一定会降低猜测难度。我们必须要证明，在整个猜测序列中，重复项所占的比重是”可忽略“的。
首先让我们放下这个目标，来考虑一个经典问题：你邀请了很多朋友（假如q个）来参加你的生日派对，那么他们之中有两人生日恰好同一天（假设一年有N天）的概率是多少？这个概率是\(1-(1-\frac{1}{N})*...*(1-\frac{q}{N})\)，事实上，当N=365时，q=23时概率就能超过50%，q=70时概率就能超过99.99%！
这和我们的目标有什么关系？我们每请一位朋友来派对，就相当于调用了一次函数；当我们发现有两位朋友的生日相同，就相当于发现函数的输出相同；N就相当于我们的结果空间，而q就是猜测次数。我们需要证明，当一年的长度可以被指数空间所描述时，我们仅邀请多项式级别数量的朋友来派对，是无法发现有两人恰好同一天生日的。
我们可以证明生日派对问题的概率满足以下上下界：
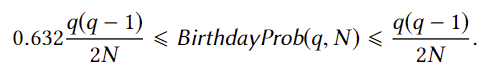
由于q是多项式级别的，因此\(q^2\)也是多项式级别的，而\(N\)是指数级别的，也就是说发现同一天生日的人的概率满足我们对”可忽略“的定义！这就意味着即使我们从猜测序列中去除重复项，也不会影响对安全性的判断！
我们再讨论一种情况：此时我们每次放回取样，但是会避开特定的元素（这个集合的长度应该是多项式级别的，假设第i次取样会避开特定的\(n_i\)个元素），那么最终我们可以得到在原放回取回函数和新的函数之间尝试\(q\)次，发现函数输出存在差异的概率是\(\prod_{i}^{q}(1-\frac{n_i}{N})\)，可以证明这个概率同样符合”可忽略“定义。机智的你一定能发现，假如我们设\(n_i=i-1\)，那么这就和生日派对问题完全一样了！
