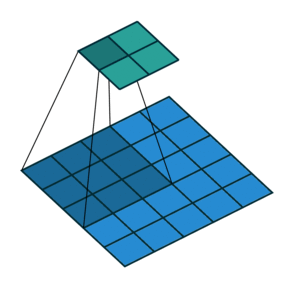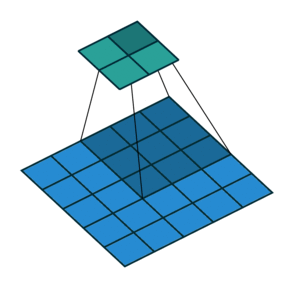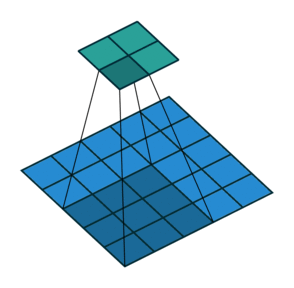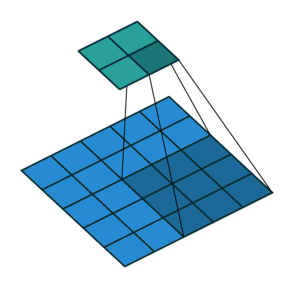
卷积神经网络卷积核滑窗计算

1. 定义背景

• 卷积核（Kernel/Filter）：一个小矩阵，用于提取特定的特征，比如边缘、纹理等。
• 图像：可以表示为一个二维矩阵，其中每个元素是像素值。

操作步骤：

1. 卷积核覆盖到图像的某一区域（子矩阵）。
2. 卷积核和图像的子矩阵对应位置逐元素相乘。
3. 将乘积求和，得到一个单一值。
4. 按一定步幅（stride）移动卷积核，重复上述操作，生成一个输出矩阵（特征图）

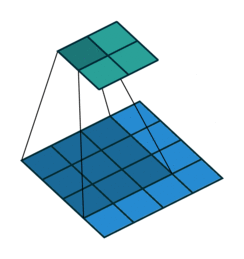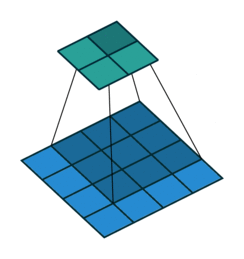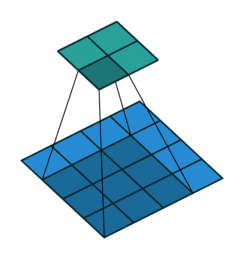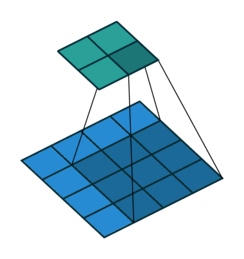
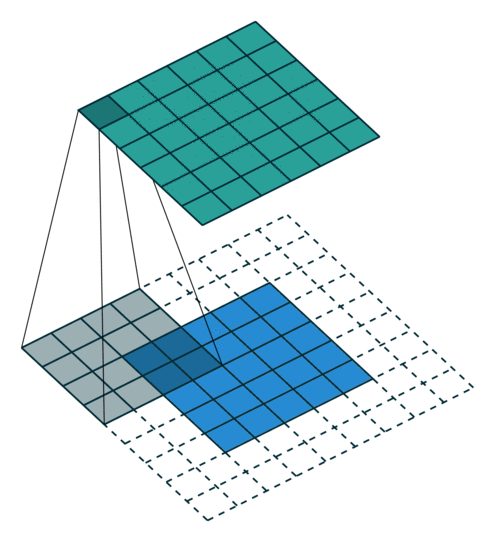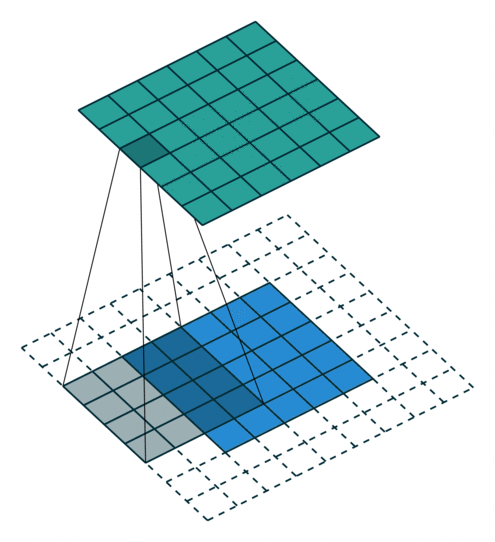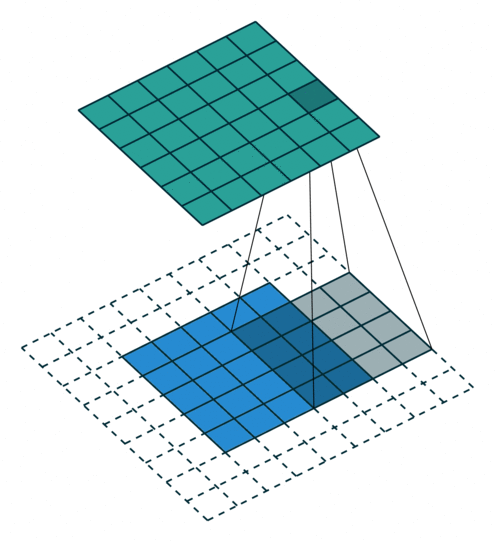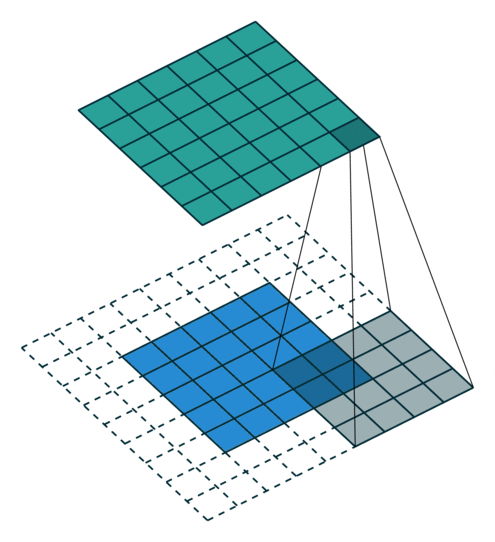
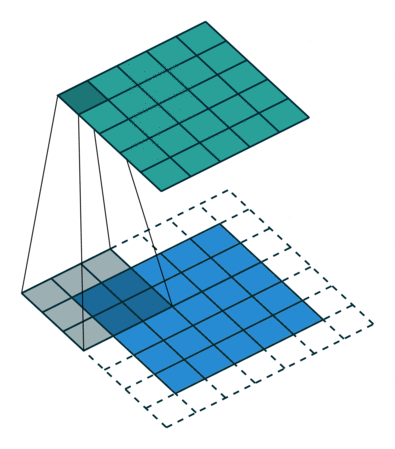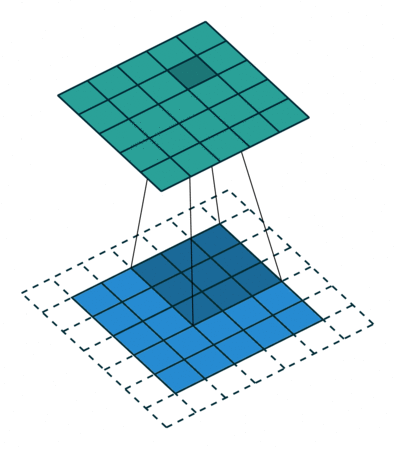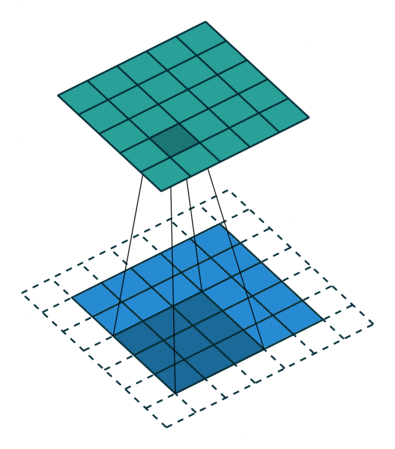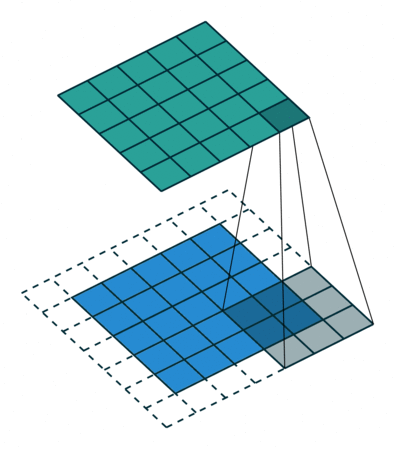
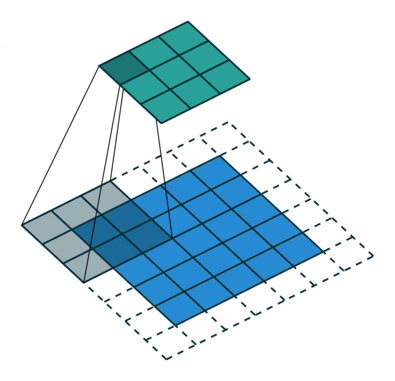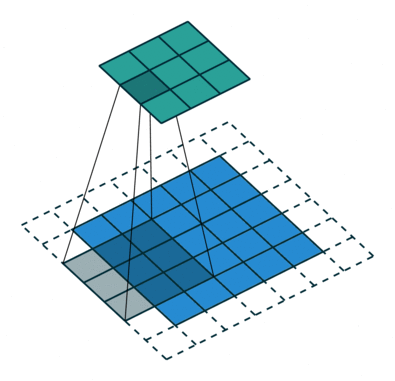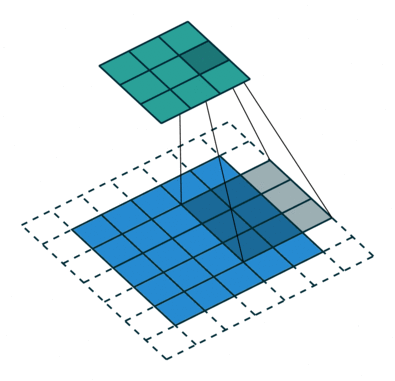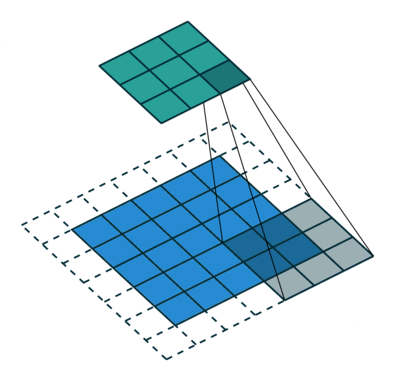
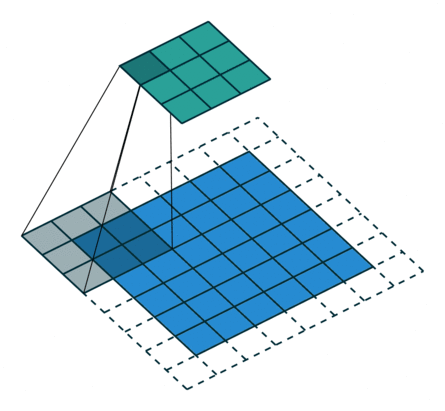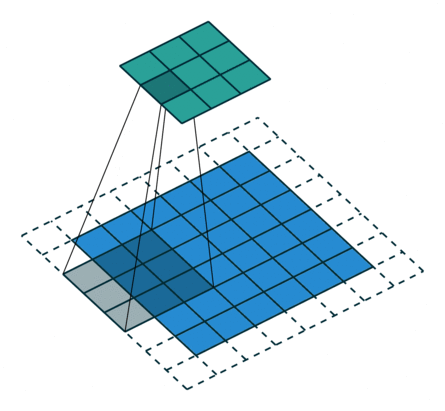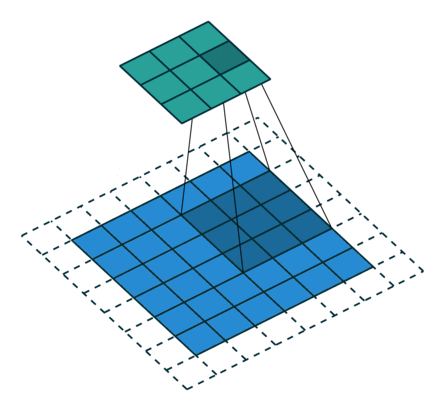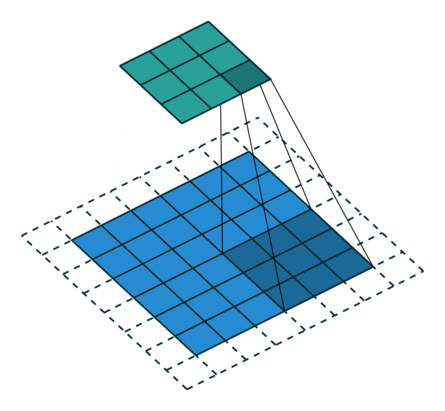
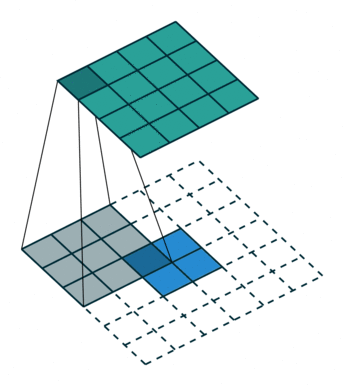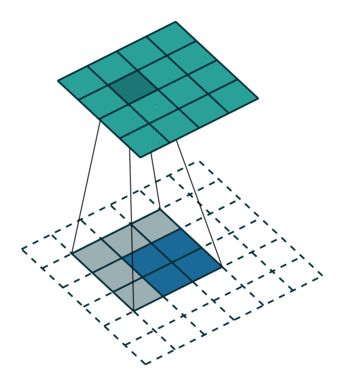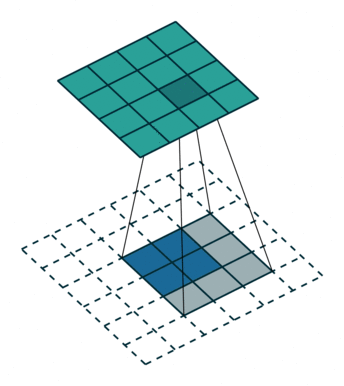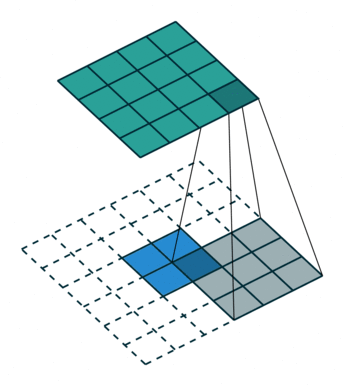
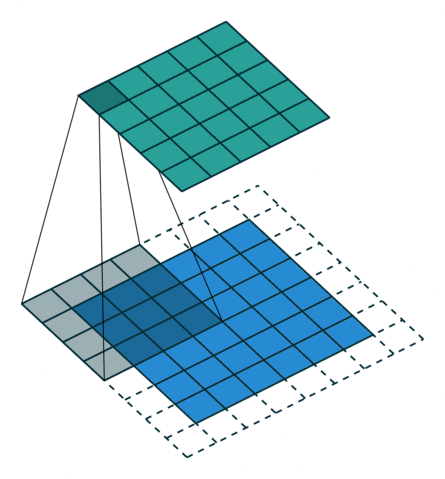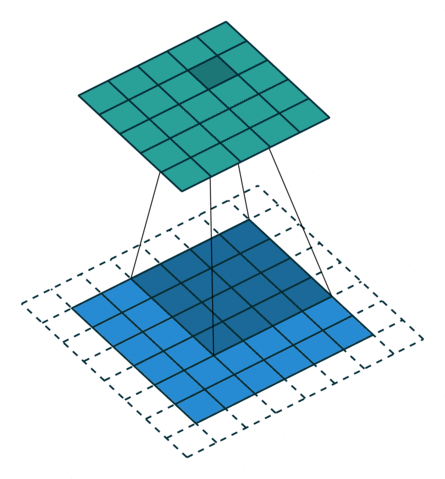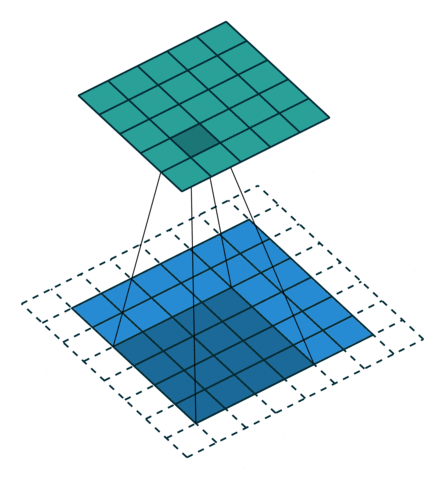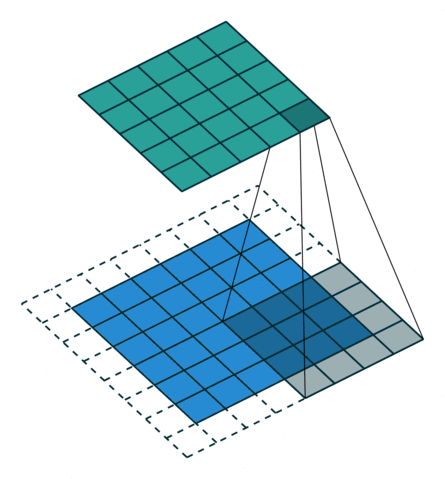
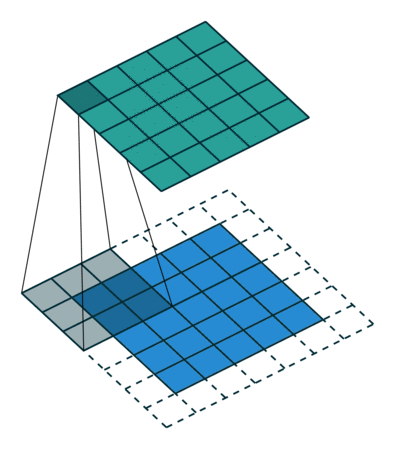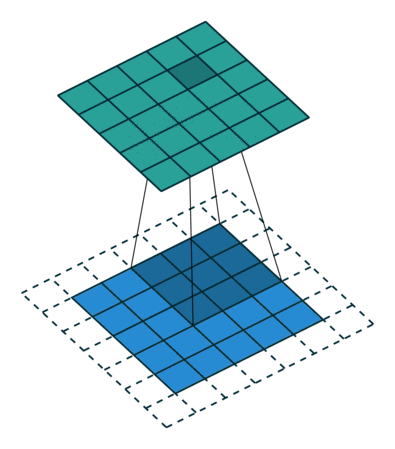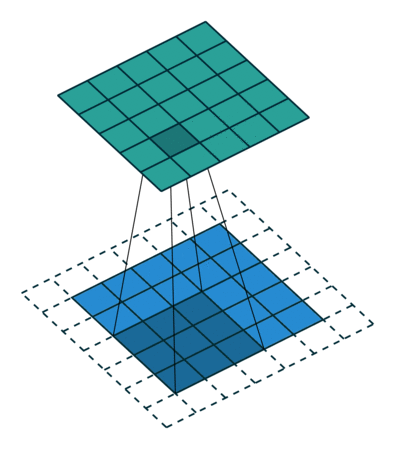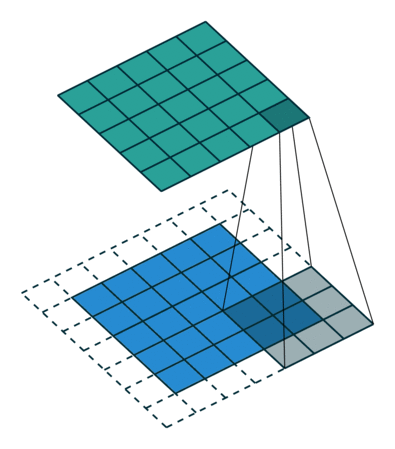
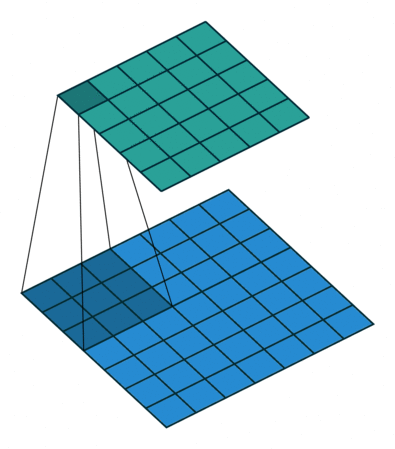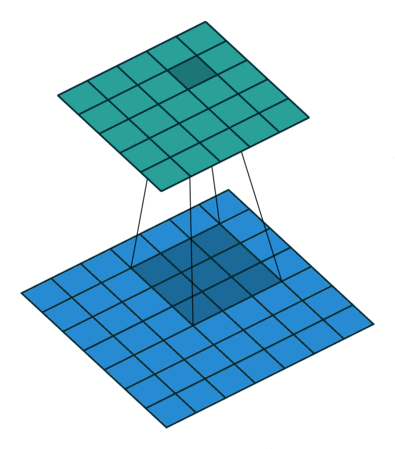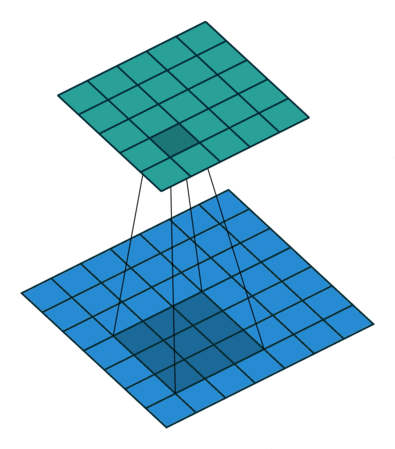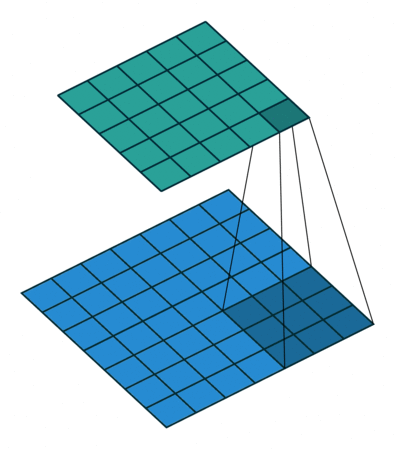
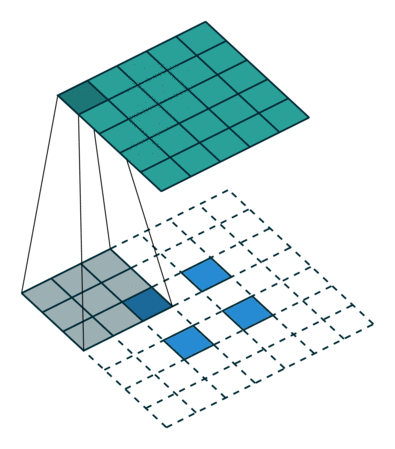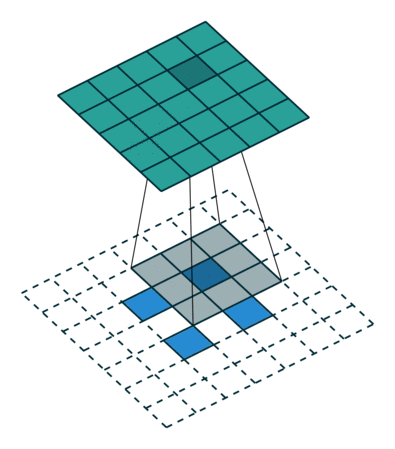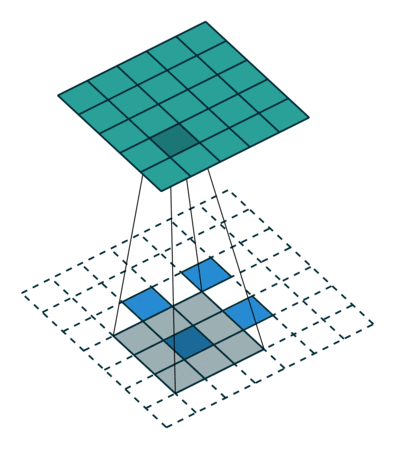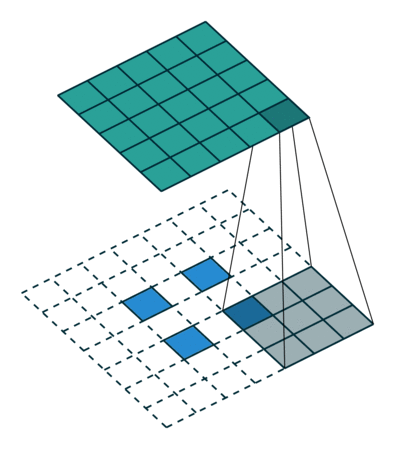
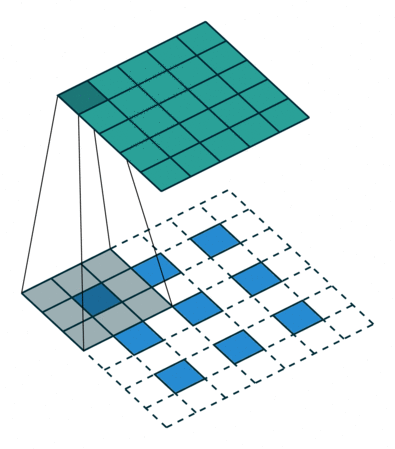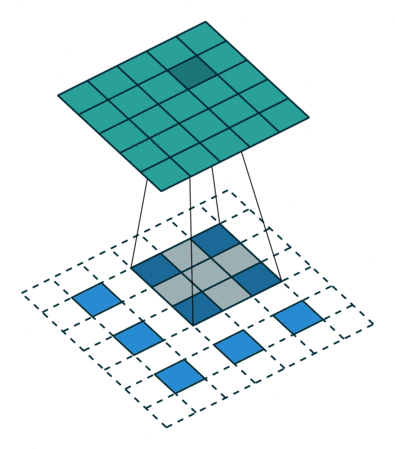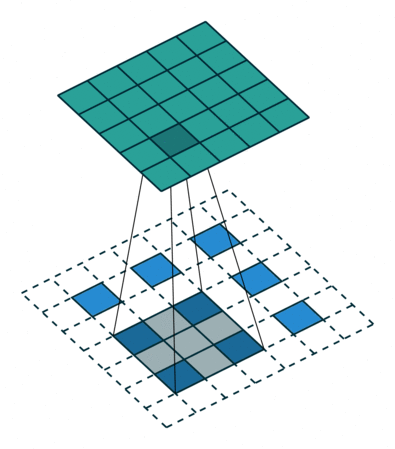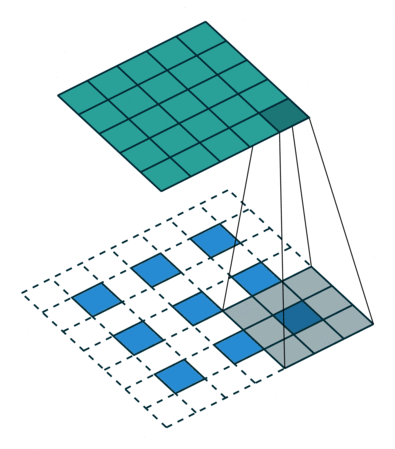
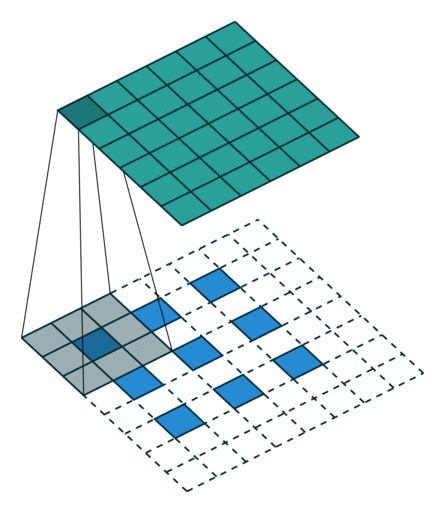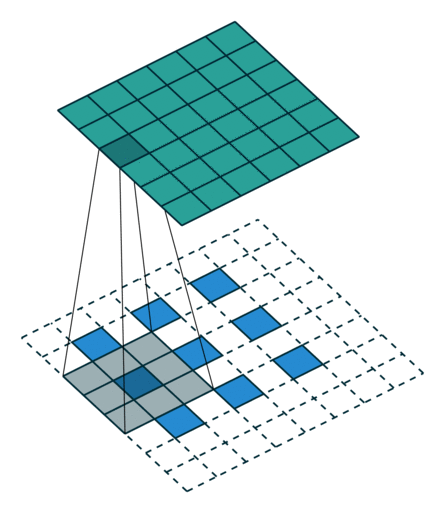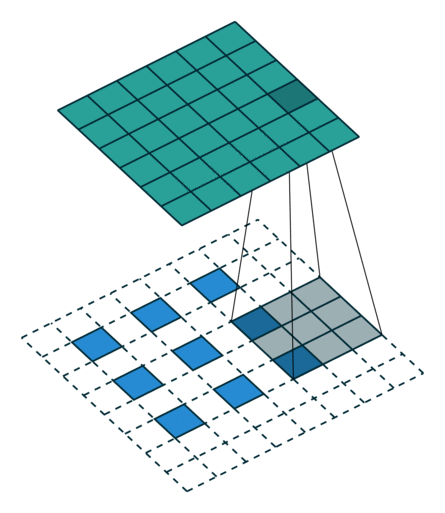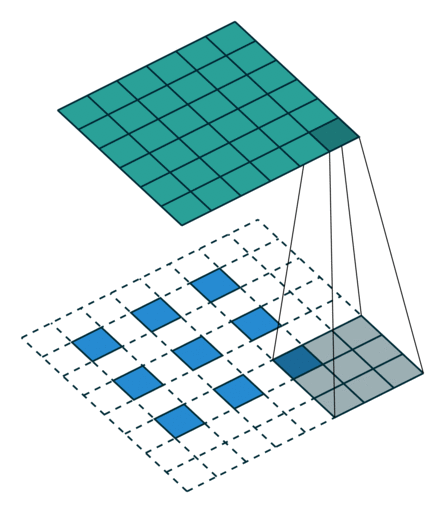
卷积动画

蓝色是输入矩阵，青色是输出矩阵

No padding, no strides	Arbitrary padding, no strides	Half padding, no strides	Full padding, no strides
No padding, strides	Padding, strides	Padding, strides (odd)

 

 

转置卷积动画

蓝色是输入矩阵，青色是输出矩阵

 

No padding, no strides, transposed	Arbitrary padding, no strides, transposed	Half padding, no strides, transposed	Full padding, no strides, transposed
No padding, strides, transposed	Padding, strides, transposed	Padding, strides, transposed (odd)

 

 

假设：

• 图像矩阵：

​

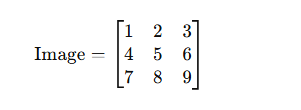
• 卷积核：

 

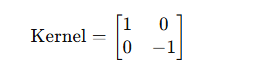
• 卷积操作采用：
  • 步幅 stride=1 
  • 无填充（padding）。

---

第一步：计算第一个位置

卷积核与图像左上角的 2×2  子矩阵重叠：

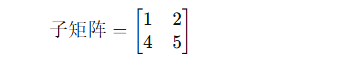
然后子矩阵和卷积核矩阵点乘：

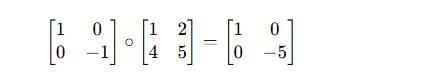
然后求和：

1+0+0−5=−4

输出矩阵第一个元素为 −4。

 

 

---

第二步：计算第二个位置

卷积核向右移动一步，与图像的另一个 2×2 子矩阵重叠：

点乘：

然后求和：

2+0+0−6=−4

输出矩阵第二个元素为 -4

---

 

第三步：计算第三个位置（下一行）

卷积核继续按步幅移动，重复上述操作，最终生成一个 ：

输出矩阵

---

 

最终输出矩阵

输出矩阵的大小取决于输入图像、卷积核的大小以及步幅、填充。对于本例，最终输出为：

卷积操作的数学本质

卷积核和子矩阵之间的逐元素相乘求和，可以看成是向量化的内积运算。如上面例中的

上面卷积核，子矩阵都是一个2x2的矩阵，卷积核向量化 A =（1 ,0 , 0 ,-1） 子矩阵向量化 B =（2 , 3, 5, 6）

A和B 内积运算 = 卷积核和子矩阵逐元素相乘求和 。

将这些乘积求和后，得到的值代表该局部区域的“特征强度”或“关系量”，并存储在输出特征矩阵中对应的位置。比如上面给出的卷积运算

所以卷积计算也就是针对子矩阵的特定转换，比如：

平均滤波器

 这种滤波器对图像的高频部分（比如边缘和细节）产生衰减，而保留低频成分（整体亮度和大范围变化）。因为局部区域卷积计算后新的值都是相邻9个像素灰度值的和。使原图中的差异变得平缓。

高通滤波器（增强边缘）

 这种滤波器对高频部分的响应更强，突出图像的边缘和快速变化的区域。局部区域的9个像素点中心点值增大8倍然后减去周围8个点的值，扩大中心点与周围像素的差异化。

卷积操作的应用

滑动窗口的算法，比如卷积操作，其抑制某些波段（或者增强某些波段）的能力源于卷积核的设计和它对输入信号的频率响应。这是信号处理和滤波理论的核心概念。

 

 

水平边缘检测

 上图是一个6x6的像素值的图片，计算机中该图片的灰度值矩阵为：

 

 

​

水平边缘检测卷积核（kernel）为：

Step 1: 窗口位置和计算公式

取3×3 子矩阵：

逐元素与卷积核相乘并求和：

 

---

Step 2: 完整特征矩阵计算

依次计算每个滑动窗口的卷积值：

类似计算下去，得到完整的 4×4 的特征矩阵：

---

特征矩阵

为什么结果一致？

• 卷积核的设计（检测水平边缘）和图像的结构使得每个位置的水平边缘强度相同，因此特征矩阵中的值一致。

​​

计算机