代码随想录——动态规划31打家劫舍III（树状DP）

合集 - 代码随想录(35)

1.代码随想录-逆波兰式、滑动窗口最大值2024-10-292.代码随想录-栈与队列-有效的括号（括号匹配）2024-10-263.代码随想录——栈与队列8-前K个高频元素2024-10-304.二叉树的递归遍历和迭代遍历2024-11-085.代码随想录——二叉树-11.完全二叉树的节点个数2024-11-116.代码随想录——二叉树-12.平衡二叉树2024-11-117.代码随想录——二叉树17-路径总和2024-11-138.代码随想录——二叉树19.最大二叉树2024-11-219.代码随想录——二叉树21、合并二叉树（附：递归算法复杂度分析）2024-11-2210.代码随想录——二叉树23、验证二叉搜索树2024-11-2211.代码随想录——25二叉搜索树的最小绝对值差（递归遍历如何记录前后两个指针）2024-11-2512.代码随想录——25.二叉搜索树中的众数2024-11-2513.代码随想录——26、二叉(搜索)树的最近公共祖先2024-11-2614.代码随想录——回溯8、组合总和II2024-12-0415.代码随想录——回溯9.分割回文串2024-12-0516.代码随想录——回溯19重新安排行程2024-12-1217.代码随想录——回溯 N皇后2024-12-1418.代码随想录——贪心8.跳跃游戏II2024-12-1619.代码随想录——贪心9.K次取反后最大化的数组和 && std::sort函数的第三个参数说明2024-12-1620.代码随想录——贪心13.分发糖果2024-12-1721.代码随想录——贪心算法：根据身高重建队列 & Vector原理2024-12-2322.代码随想录——贪心算法22单调递增的数字2024-12-2523.代码随想录——贪心23监控二叉树2024-12-2624.代码随想录——动态规划5.周总结2024-12-2625.代码随想录——动态规划9不同的二叉搜索树2024-12-2826.代码随想录——动态规划01背包2024-12-2927.代码随想录——动态规划13.分割等和子集2024-12-2928.代码随想录——动态规划14最后一块石头的重量II（01背包）2024-12-3029.动态规划——dp的含义归类（完全背包和01背包区别）01-1930.动态规划——26单词拆分01-1931.代码随想录——动态规划背包问题总结01-19

32.代码随想录——动态规划31打家劫舍III（树状DP）01-20

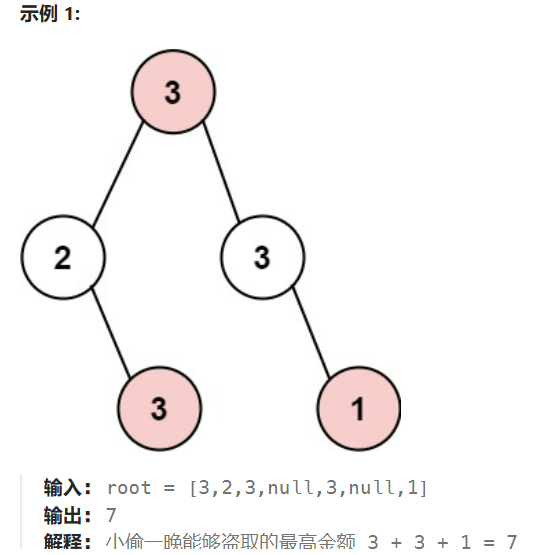
33.代码随想录——动态规划、股票问题01-2334.代码随想录——单调栈02-0535.回溯总结02-11

收起

这道题目是 打家劫舍 III（House Robber III），是打家劫舍系列问题的变种。问题描述如下：

小偷发现了一个新的区域，这个区域的所有房屋排列类似于一棵二叉树。如果两个直接相连的房屋在同一晚被打劫，房屋会自动报警。给定这棵二叉树的根节点 root，求在不触发警报的情况下，小偷能够盗取的最高金额。

---

题目思路

1. 问题分析

• 每个节点（房屋）有两个状态：偷 或 不偷。
• 如果偷了当前节点，则不能偷其直接子节点（左子节点和右子节点）。
• 如果不偷当前节点，则可以偷其子节点，也可以选择不偷子节点。
• 目标是找到一种偷窃方案，使得总金额最大。

---

2. 解题方法

这道题有两种常见的解法：

1. 记忆化搜索 + 递归
2. 树形动态规划（树形DP）

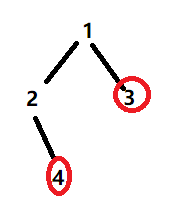
不能用层序遍历化为一维数组再套用前面的打家劫舍。如以下情况不能解决

---

方法一：记忆化搜索 + 递归

思路

• 对于每个节点，有两种选择：
  1. 偷当前节点：不能偷其左右子节点，但可以偷其孙子节点（左右子节点的子节点）。
  2. 不偷当前节点：可以考虑偷其左右子节点。
• 使用递归计算这两种选择的最大值。
• 记忆化搜索：每次偷爷爷节点时，又要重新计算孙子节点。但在此之前孙子节点已经计算过了。为了避免重复计算，使用 unordered_map<TreeNode*, int> 进行记忆化存储。

之前记忆化搜索一般使用数组（如斐波那契数列）缓存。但二叉树不适合拿数组当缓存，我们这次使用哈希表来存储结果

代码实现

class Solution {
public:
    unordered_map<TreeNode*, int> mp; // 记忆化存储

    int rob(TreeNode* root) {
        if (root == nullptr) return 0; // 空节点，返回0
        if (mp[root]) return mp[root]; // 如果已经计算过，直接返回

        // 偷当前节点
        int val1 = root->val;
        if (root->left) val1 += rob(root->left->left) + rob(root->left->right); // 偷孙子节点
        if (root->right) val1 += rob(root->right->left) + rob(root->right->right); // 偷孙子节点

        // 不偷当前节点
        int val2 = rob(root->left) + rob(root->right); // 偷子节点

        mp[root] = max(val1, val2); // 记录当前节点的最大值
        return mp[root];
    }
};

复杂度分析

• 时间复杂度：O(n)，其中 n 是节点数量。每个节点只会被计算一次。
• 空间复杂度：O(n)，用于存储记忆化结果和递归栈。

---

方法二：树形动态规划（树形DP）

方法一还要考虑孙子节点，能不能只考虑儿子——>记录每个节点选/不选的状态最大值

思路

• 对于每个节点，返回一个长度为 2 的数组 dp：
  • dp[0]：不偷当前节点时的最大金额。
  • dp[1]：偷当前节点时的最大金额。
• 通过后序遍历（左右根）计算每个节点的 dp 值。
• 最终结果是根节点的 dp[0] 和 dp[1] 的最大值。

代码实现

• 树形DP在树上进行状态转移，因此需要递归实现

class Solution {
public:
    int rob(TreeNode* root) {
        vector<int> result = robTree(root);
        return max(result[0], result[1]); // 返回偷或不偷根节点的最大值
    }

    vector<int> robTree(TreeNode* root) {
        if (root == nullptr) return {0, 0}; // 空节点，返回 {0, 0}

        vector<int> left = robTree(root->left); // 左子树的 dp 值
        vector<int> right = robTree(root->right); // 右子树的 dp 值

        // 不偷当前节点：左右子树可偷可不偷
        int val0 = max(left[0], left[1]) + max(right[0], right[1]);
        // 偷当前节点：左右子树不可偷
        int val1 = root->val + left[0] + right[0];

        return {val0, val1}; // 返回当前节点的 dp 值
    }
};

复杂度分析

• 时间复杂度：O(n)，每个节点只会被访问一次。
• 空间复杂度：O(n)，递归栈的深度最大为树的高度。

---

方法对比

方法	优点	缺点
记忆化搜索 + 递归	直观，易于理解	需要额外的空间存储记忆化结果
树形DP	空间效率更高，无需额外存储	需要理解状态转移方程

---

总结

• 记忆化搜索 + 递归：通过递归遍历树，同时使用 unordered_map 存储中间结果，避免重复计算。
• 树形DP：通过后序遍历，返回每个节点的状态值（偷或不偷），最终选择最大值。

两种方法的时间复杂度都是 O(n)，但树形DP的空间效率更高，推荐使用树形DP。