用python来炒股<三> 炒股交易系统(法则)

逢高买入法

I.假设处在在一段上升行情中，a 处买入后，在e处为最高点，当价格再次跌至d处全部卖出。

1. 若全程仅购入单份x且在a处，则获利为 (d- a)* x = 3px

2. 若全程在每个分点均购入x，则获利为3px+2px = 5px

   另外，若考虑分摊成本量，即近似认为将x 总量分散为x/5, 则获利为3p*x/5 +2p*x/5 =px

因此，单位总量不变的情况下，普通上涨行情中不适合分批多次买入

II. 假设在一段极强的行情中，a处之后在第13个节点时为最高点。同样的可以得出：

1. 全程单次买入获利为 (12p -1p)x =11px

2. 全程分段买入获利为(12-1)px/13 +(12-2)px/13 + .... +(12-10)px/13 = 55px/13

 

 

逢低买入法

假设在一段下跌行情中，每到一个低点买入

1. 单笔买入时在b处回升，则获利为 0px =0 

2. 分笔买入时在b处回升，则获利为 0px/2+1px/2 =px/2

若出现极低行情 至e处

1. 单笔买入在e处回升，则获利为 (d-a)x = -3px

2. 分笔买入在e处回升，则获利为-3px/5-2px/5-1px/5+0px/5+1px/5 = -px

进一步认为，在下跌途中分批买入能减小损失

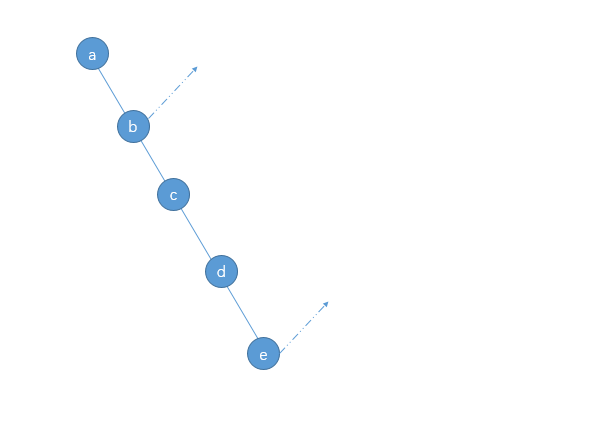
 若存在行情震荡

1. 逢高买入法：a为起点，需c处，d处买入，截至e处时，总获利 (e-a)x+(e-c)x+(e-d)x 。当e = a时，此时获利简化为 （a-c）px +（a-d）px < 0 

2. 逢低买入法：a为起点，在b处买入，总获利为(e-b)x+(e-a)x 。当e =a 时，此时获利简化为 (a-b)x >0

3. 单笔买入：a为起点，其他位置不参与，截止e处时，总获利(e-a)x。当e =a时，此时获利简化为 0 

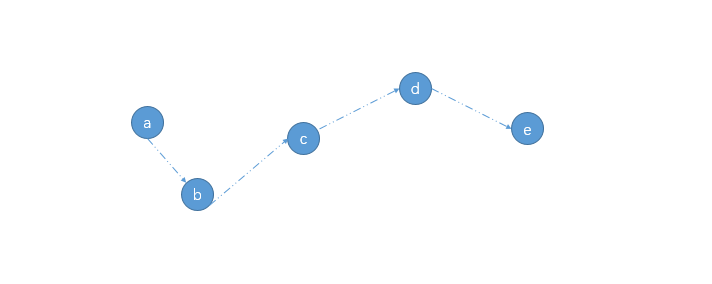
 若为普通的震荡上行行情

 

 

 

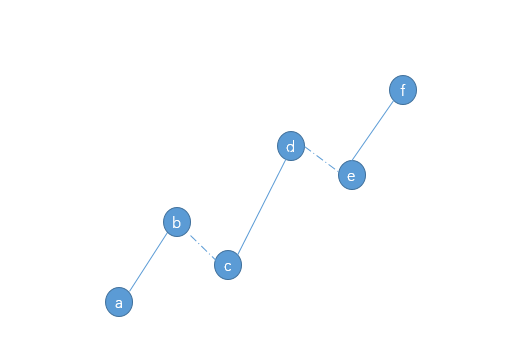
1. 逢高买入法：a为起点，需b处，d处买入，截至f处时，总获利S逢高 (f-a)x+(f-b)x+(f-d)x 。

2. 逢低买入法：a为起点，在c处, e处买入，总获利为S逢低= (f-e)x+(f-c)x+(f-a)x 。

由于c<b, e<d, 则S逢低》 S逢高，说明为相比较而言，在普通行情上涨过程中不适合追高，但更适合回调买入

3. 单笔买入：a为起点，其他位置不参与，截止f处时，总获利S单买 = (f-a)x

考虑到行情初期，不太重仓操作，因此S逢低实际中的x 单位为θx, 即为了 (f-a) > θ[(f-a)+(f-c)+(f-e)]

当资金划分为o等分，且完全投入，θ(a+c+e)>a, 其中θ<=1/3, c+e>2a

总结：只要c，e 不跌破前期a 点，单笔买入更划算。

意义：

单笔上升或者震荡上升的行情，最佳建仓仅有一次，且需重仓。若错过最近重仓位置，则在回调且不跌破前最佳位置点最为适宜。