一阶低通滤波算法在电机控制中的使用

前言

推导的思路是从物理电路到软件实现

一阶RC滤波器

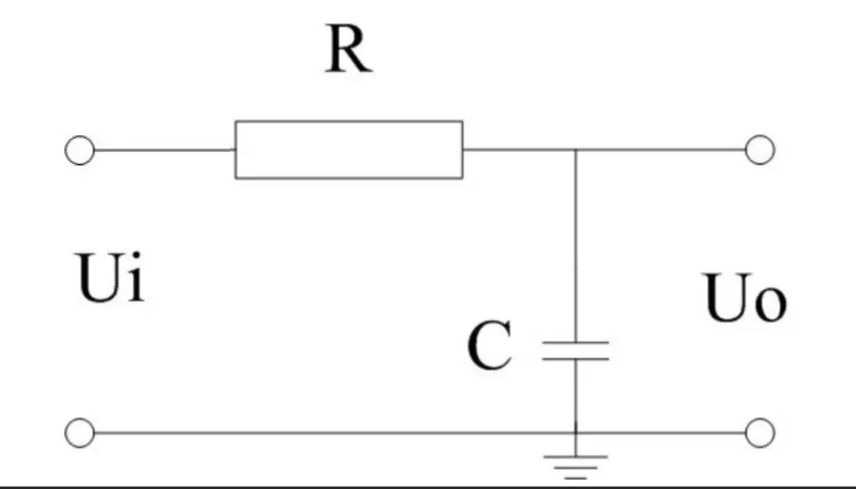
从这个经典的电路开始分析，首先是输入\(u_1\)和输出\(u_2\) 的表达式

由公式

\(i(t) = \frac{C du(t)}{dt}\)

\(u(t) = \frac{L di(t)}{dt}\)

\(u_i = RC*\frac{d u_o(t)}{dt}+u_o\)

首先转到S域

\(u_i(s) = RCSu_o(s)+u_o(s)\)

传递函数\(\frac{u_o(s)}{u_i(s)} = \frac{1}{RCS+1}\)

一个问题，为啥\(\frac{1}{RC}被称为截止频率\)：

求解该传递函数的幅频响应 \(|H(jw)| = |\frac{1}{RCjw+1}| = \frac{1}{1+(RCw)^2}\)

当\(\frac{u_o(s)}{u_i(s)} = \sqrt{\frac{1}{2}}\) 时此时的频率就称为截至频率，也就是上面表达式中\(RCw = 1\)；也就是当输入的频率 \(w=\frac{1}{RC}\)
注意这里 \(w\) 的单位是\(rad/s\) 转换成 \(hz\), \(2πrad/s = 1hz\)

离散化

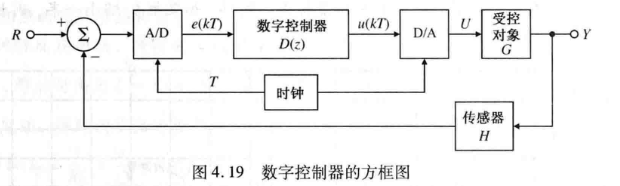
离散化的推导，Z变换的由来，S域变换到Z域，

离散化方法

$Z = e^{-TS}$ 根据位移定理就是相当于离散的采样。

• 前向差分 变换后不能保证系统的稳定 \(S = \frac{Z-1}{T_s}\)

• 后向差分 \(S = \frac{Z-1}{ZT_s}\)

• 双线性变换 （tustin方法）\(S = \frac{2(Z-1)}{T_s(Z+1)}\)

• 零极点匹配法

• 改进的零极点匹配法

示例

我们在S域根据传递函数进行控制器的设计，然后使用把S域转换到Z域中离散化，最后在由Z域转化时域的微分方程，完成设计。在进行后向差分或双极性变换的时候需要注意一个技巧，需要把Z的指数全部变换成负数的，（分子分母同除以最高的Z的指数项）这样就可以比较直观的套用Z变换的位移定理，\(Z^{-1}Y(Z) = y(t-1)\),以此类推。
那么就以上面是一阶级低通滤波器为例,设计一个带宽是100HZ的低通滤波器。

\(\frac{u_o(s)}{u_i(s)} = \frac{1}{RCS+1}\)

这里使用matlab辅助计算，使用tustin的方式逼近

T = sym('T') 
z = sym('z');
RC = sym('RC');
s = (2*(1-z^(-1)))/(T*(1+z^(-1)));
% f = 100*2*pi;%带宽100hz
% RC = 1/f;
G(z) = (1/(1+RC*s))
G1 = simplify(G)
[num, den] = numden(G);

运行结果\(G1(Z) = \frac{u_o(Z)}{u_i(Z)}= \frac{T*(Z + 1)}{T - 2*RC + 2*RC*Z + T*Z} =\frac{T*(1+Z^{-1})}{T*Z^{-1}-2*RC*Z^(-1)+2*RC+T}\)
转换成差分方程
\(T*u_o(Z)*Z^{-1}-2*RC*u_o(Z)*Z^{-1}+2*RC*u_o(Z)+T*u_o(Z) = T*u_i(Z)+T*u_i(Z)Z^{-1}\)

\(T*u_o(t-1)-2*RC*u_o(t-1)+2*RC*u_o(t)+T*u_o(t) = T*u_i(t)+T*u_i(t-1)\)

\(u_o(t) = \frac{T}{2RC+T}*u_i(t)+\frac{T}{2RC+T}*u_i(t-1)+ \frac{2RC-T}{2RC+T}u_o(t-1)\)

simulink 仿真

• 仿真模型，采样时间0.001s，带宽100hz

  

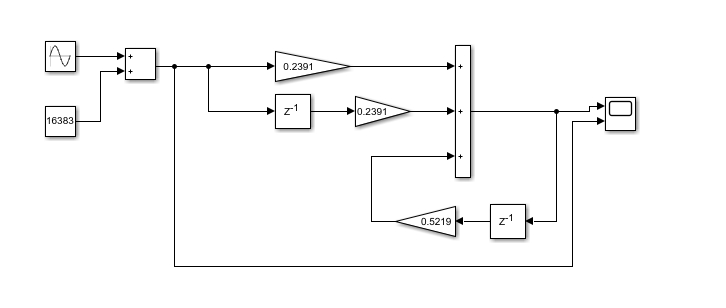
• 伯德图

  

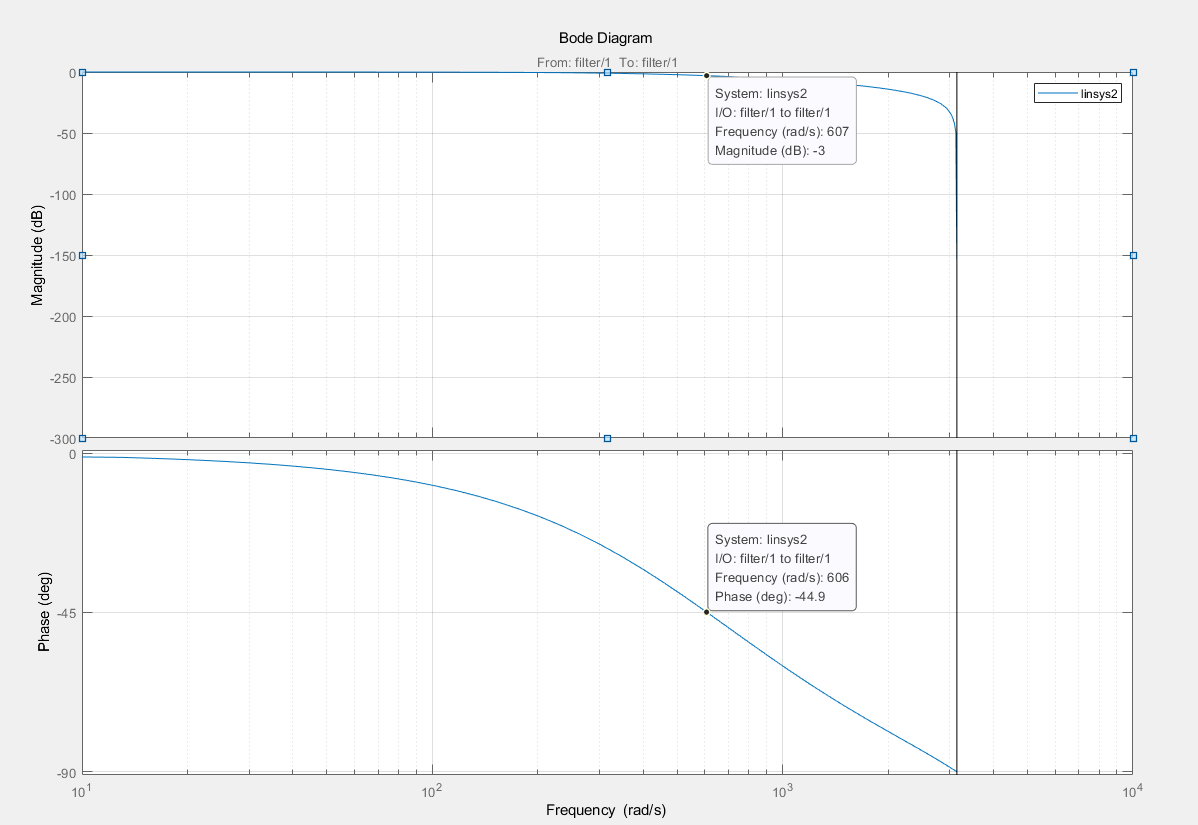
前向差分变换后不能保证系统的稳定，比较常用的是后向差分和双线性变换

C语言实现

/*参考上面simulink仿真实现即可*/