遗传算法
基本概念
- 染色体:待解决的数学问题的一个可行解成为染色体。
- 基因:一个可行解一般由多个元素构成,那么这每一个元素就被称为染色体上的一个基因。
- 适应度函数:执行优胜劣汰的函数。将适应度高的染色体留下,将适应度低的染色体淘汰掉。从而经过若干次迭代后染色体的质量将越来越优良。
- 交叉:两个染色体生成一个新的染色体,新染色体上的基因由轮盘赌算法完成。在每完成一次进化后,都要计算每一条染色体的适应度,然后采用公式计算每一条染色体的适应度概率。那么在进行交叉过程时,就需要根据这个概率来选择父母染色体。适应度比较大的染色体被选中的概率就越高。这也就是为什么遗传算法能保留优良基因的原因。(染色体i被选择的概率 = 染色体i的适应度 / 所有染色体的适应度之和)
- 变异:交叉能保证每次进化留下优良的基因,但它仅仅是对原有的结果集进行选择,基因还是那么几个,只不过交换了他们的组合顺序。这只能保证经过N次进化后,计算结果更接近于局部最优解,而永远没办法达到全局最优解,为了解决这一个问题,我们需要引入变异。变异很好理解。当我们通过交叉生成了一条新的染色体后,需要在新染色体上随机选择若干个基因,然后随机修改基因的值,从而给现有的染色体引入了新的基因,突破了当前搜索的限制,更有利于算法寻找到全局最优解。
- 选择:淘汰fw个体,选出优秀个体传给下一代。
- 表现型:输入的值。
- 基因型:将输入值编码后的值。故表现型通过编码变成基因型,基因型通过解码变成表现型。
- 编码方式:分为二进制编码,实数编码和符号编码。
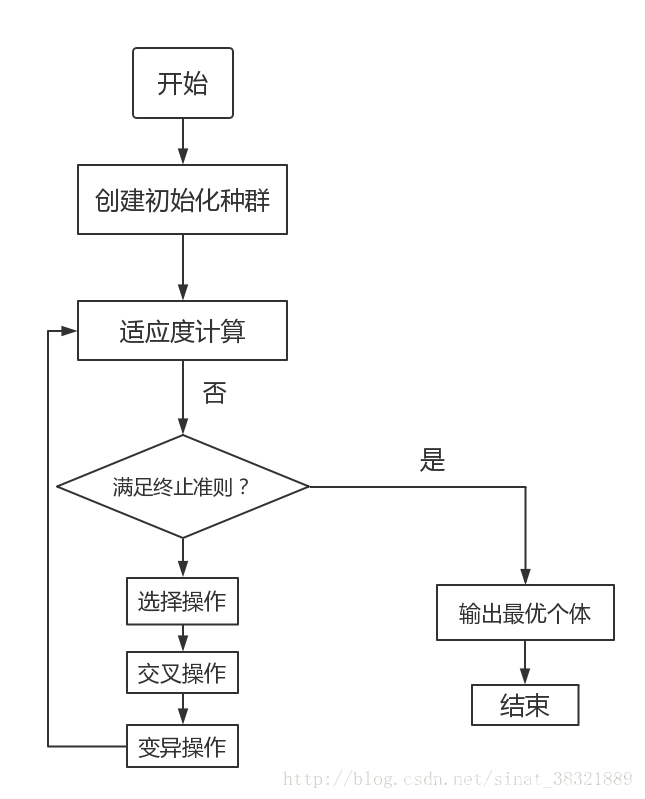
算法
流程
- 在算法初始阶段,它会随机生成一组可行解,也就是第一代染色体。
- 然后采用适应度函数分别计算每一条染色体的适应程度,并根据适应程度计算每一条染色体在下一次进化中被选中的概率。
- 通过“交叉”,生成N-M条染色体;
- 再对交叉后生成的N-M条染色体进行“变异”操作;
- 然后使用“复制”的方式生成M条染色体;
流程图如下:
遗传算法工具箱
从界面运行 APP - Optimization app,然后从 Solver 菜单选择ga - Genetic Algorithm。
遗传算法工具箱是求最小值的,最大值的话就添负号。
代码
求 $f(x)=x+10sin(5x)+7cos(4x),x∈[0,10] $ 的最大值。
步骤
- 初始化种群
- 计算目标函数值和适应度值:目标函数的结果可以是负数,但是适应度值不能为负数。因为后面会用轮盘赌法算概率,如果适应度值为负数的话,概率也为负数。母猪会上树概率都不可能为负数。所以,要进行处理,当目标函数为负数时候适应度值要为0。
- 选择,交叉,变异
- 求最优个体,并记录
- 继续下一次迭代,直到迭代结束
- 根据每一次迭代的最优个体,再找出其中的最优个体,即为最优解
主程序
clear
clc
popsize=20; %群体大小
chromlength=10; %字符串长度(个体长度)
pc=0.6; %交叉概率,只有在随机数小于pc时,才会产生交叉
pm=0.001; %变异概率
times = 2000 % 遗传次数
pop=initpop(popsize,chromlength); %随机产生初始群体
for i=1:times
[objvalue]=calobjvalue(pop); %计算目标函数
fitvalue=calfitvalue(objvalue); %计算群体中每个个体的适应度
[newpop]=selection(pop,fitvalue); % 选择
[newpop1]=crossover(newpop,pc); % 交叉
[newpop2]=mutation(newpop1,pm); % 变异
[objvalue]=calobjvalue(newpop2); %计算目标函数
fitvalue=calfitvalue(objvalue); %计算群体中每个个体的适应度
[bestindividual,bestfit]=best(newpop2,fitvalue); %求出群体中适应值最大的个体及其适应值
y(i)=bestfit; %返回的 y 是自适应度值,而非函数值
x(i)=decodebinary(bestindividual)*10/1023; %将自变量解码成十进制
pop=newpop2;
end
fplot('x+10*sin(5*x)+7*cos(4*x)',[0 10])
hold on
plot(x,y,'r*')
hold on
[z ,index]=max(y); % 计算所有最优良个体中的最优良个体
x5=x(index) % 计算最大值对应的x值
ymax=z
初始化 initpop.m
根据种群大小和个体长度构造个全为0和1的随机二进制编码基因的种群,同时这个种群每一横行表示一个个体。此例的矩阵为20*10。
function pop=initpop(popsize,chromlength)
pop=round(rand(popsize,chromlength));
计算目标函数值 calobjvalue.m
将基因型转换为表现型。
function [objvalue]=calobjvalue(pop)
temp1=decodebinary(pop); % 将pop每行转化成十进制数
x=temp1*10/1023; % 得到十进制数在0~1023之间,通过变换得到x属于0~10的值
objvalue=x+10*sin(5*x)+7*cos(4*x); % 通过x的值计算目标函数值
如果是和神经网络连用的话,神经网络输入值归一化的值就在0到1之间,所以只用将转换的十进制数除以1023然后就可以代入网络中。
除了把二进制数看作是二进制整数外,我还有个思路就是把二进制数看成小数,这样的话转换成十进制数的时候本来就在0~1之间,这样就不用再处理了。
二进制转换为十进制 decodebinary.m
sum函数第二个参数不写默认是1,表示对每一列求和得到行向量。如果第二个参数输入2,则表示对每一行求和得到列向量。
function pop2=decodebinary(pop)
[px,py]=size(pop); %求pop行和列数
for i=1:py
pop1(:,i)=2.^(py-i).*pop(:,i);
end
pop2=sum(pop1,2); %求pop1的每行之和
适应度函数 calfitvalue.m
如果目标函数值大于等于0,适应度是目标函数值。如果目标函数值小于0,适应度就是0。
function fitvalue=calfitvalue(objvalue)
[px,py]=size(objvalue); %目标值有正有负
for i=1:px
if objvalue(i)>0
temp=objvalue(i);
else
temp=0.0;
end
fitvalue(i)=temp;
end
fitvalue=fitvalue';
选择 selection.m
这坨代码的思路是除掉fw个体,重复添加优秀个体,越优秀的个体添加的次数可能性越大。
function [newpop]=selection(pop,fitvalue)
totalfit=sum(fitvalue); %求适应值之和
fitvalue=fitvalue/totalfit; %单个个体被选择的概率,轮盘赌算法的公式
fitvalue=cumsum(fitvalue); % 累加是为了将分布律转换为分布函数然后可以比较
[px,py]=size(pop); %20*10
ms=sort(rand(px,1)); % 将随机数从小到大排列
fitin=1;
newin=1;
while newin<=px % 直到20个随机数被走完才跳出循环
if(ms(newin))<fitvalue(fitin) % 概率小于分布函数,优良个体被选择
newpop(newin,:)=pop(fitin,:);
newin=newin+1;
else % 概率大于分布函数,个体被淘汰,继续选择下一个个体
fitin=fitin+1;
end
end
如果这群个体中某个概率较大,则累加的数在累加到它的时候增量较大,它的增量较大几率大于随机数的增量,这个增量较大的个体会有更大的几率多次被选中。
除了上面的代码外,
交叉 crossover.m
交叉我还以为是基因的交叉,没想到是碱基对的交叉。将原来两个个体交叉出现两个新个体,然后用这两个新个体来替换掉原来的两个个体放入新的种群中。
function [newpop]=crossover(pop,pc) % pc=0.6 pc是交叉概率
[px,py]=size(pop); % px是种群数量,py是编码长度
newpop=ones(size(pop)); % 生成一群全为1的种群
for i=1:2:px-1 % 步长为2,是将相邻的两个个体进行交叉
if(rand<pc) % 如果随机数小于交叉概率,则发生了交叉
cpoint=round(rand*py); % cpoint: 0-10的随机数
newpop(i,:)=[pop(i,1:cpoint),pop(i+1,cpoint+1:py)]; % 交叉操作
newpop(i+1,:)=[pop(i+1,1:cpoint),pop(i,cpoint+1:py)]; % 交叉操作
else % 没有发生交叉newpop保持原有pop的个体
newpop(i,:)=pop(i,:);
newpop(i+1,:)=pop(i+1,:);
end
end
变异 mutation.m
随机选取一个位置,将该位置的0变成1或1变成0。
function [newpop]=mutation(pop,pm) % pop是种群,pm是变异概率
[px,py]=size(pop);
newpop=ones(size(pop));
for i=1:px
if(rand<pm) % 随机数小于变异概率,发生了变异
mpoint=round(rand*py); % 产生的变异点在1-10之间
if mpoint<=0 % 可以写成 mpoint == 0 ,因为这个值不可能小于0,但是可以等于0
mpoint=1; % mpoint表示变异位置
end
newpop(i,:)=pop(i,:);
if any(newpop(i,mpoint))==0% 这个any意义不大,因为传入的是一个值,不是矩阵
newpop(i,mpoint)=1; % 把0变异成1
else
newpop(i,mpoint)=0; % 或者把1变异成0
end
else % 不发生变异,原来的个体还是原来的个体
newpop(i,:)=pop(i,:);
end
end
求最大适应度个体 best.m
目的:将最大适应度个体保留在一个矩阵中,然后在最大适应度个体矩阵中找出其中最大适应度个体,从而获得它的x值和y值,于是它就是最大值。
function [bestindividual,bestfit]=best(pop,fitvalue)
[px,py]=size(pop);
bestindividual=pop(1,:);
bestfit=fitvalue(1);
for i=2:px
if fitvalue(i)>bestfit
bestindividual=pop(i,:);
bestfit=fitvalue(i);
end
end
自己的一些感悟
-
关于交叉:0-1编码的交叉是截取染色体部分进行交叉,实数编码的交叉是所有染色体进行随机权值相乘交叉。
-
关于选择:如果适应度是越小越好可以将适应度取倒数(或者用一个常数除以这个数,比如10)然后再用轮盘赌算法。
-
关于变异:0-1编码的变异是将1变成0,将0变成1。实数编码就是将该数加上或减去该数与上界或下界的差或和(这个随机判定)再乘以一个比较小的数,记得实数编码要检验是否在规定边界范围内。0-1编码不用检测。关于变异有一套代码:
fg = (rand*(1-num/maxgen))^2; % num:当前迭代次数。maxgen:最大迭代次数
if pick > 0.5
% chrom:种群。i:第i个个体索引。pos:变异的位置
chrom(i, pos) = chrom(i, pos)+(chrom(i, pos)-bound(pos, 2))*fg;
else
chrom(i, pos) = chrom(i, pos)+(bound(pos, 1)-chrom(i, pos))*fg;
end
参考文章
-
十分钟搞懂遗传算法:https://zhuanlan.zhihu.com/p/33042667
-
遗传算法介绍并附上matlab代码:https://www.cnblogs.com/LoganChen/p/7509702.html
-
matlab遗传工具包:https://zhuanlan.zhihu.com/p/158600868
-
一个非常好的理解遗传算法的例子 强烈推荐入门:https://blog.csdn.net/u012422446/article/details/68061932
-
【算法】超详细的遗传算法(Genetic Algorithm)解析:https://www.jianshu.com/p/ae5157c26af9
-
遗传算法(Genetic Algorithm)原理详解和matlab代码解析实现及对应gaot工具箱实现代码:https://blog.csdn.net/qq_35608277/article/details/83785678


 浙公网安备 33010602011771号
浙公网安备 33010602011771号