基于单决策树的AdaBoost
①起源:Boosting算法
Boosting算法的目的是每次基于全部数据集,通过使用同一种分类器不同的抽取参数方法(如决策树,每次都可以抽取不同的特征维度来剖分数据集)
训练一些不同弱分类器(单次分类错误率>0.5),然后将其组合起来,综合评估(默认认为每个分类器权重等价)进行分类。
AdaBoost算法进行了对其进行了改进。
一、每次训练分类器时,给予每条数据用于计算误差的不同权重D。
二、每个分类器,给予用于分类的不同权重alpha。
两种权的使用,使得AdaBoost在组合分类器时,能够根据当前的训练情况做一些调整。
②弱分类器:单决策树
单决策树应该是AdaBoost中使用最多的弱分类器。硬伤是单决策树是个0/1二类分类器。(实际是-1/+1二类)
一般决策树是通过DFS,连续选择不同维度多深度划分数据集。
单决策树就是一般决策树的1维版本,只搜dep=1就结束。
单决策树有两个好处:
一、单次分类效果很差(满足弱分类器定义)
二、根据决策属性不同,即便重复使用单决策树,也可以诞生出分类效果不同的分类器。
单决策树对于连续型数据,采用阈值(threshold)分类法。
首先确定所有数据中某个特征维度里的min/max范围。
然后采用步进的方法(每次阈值=min+当前步数*步长)来确定阈值。
基于同一个阈值,又可以把小于/大于阈值的分到不同类(2种分法)。
所以单决策树最多有【D*步数*2】种变形分类器。
②双权问题
一、分类器权alpha
定义 $\alpha = \frac{1}{2} \ln \left ( \frac{1-\varepsilon }{\varepsilon } \right )$,其中$\varepsilon$为错误率。
P.S 实际Coding时,为防止$\varepsilon$为零,通常取max($\varepsilon$,eps)
$\alpha$这个函数比较有趣,求导之后,假设每次使用新的分类器,错误率都会变小,以错误率变小为x正轴,有图像:
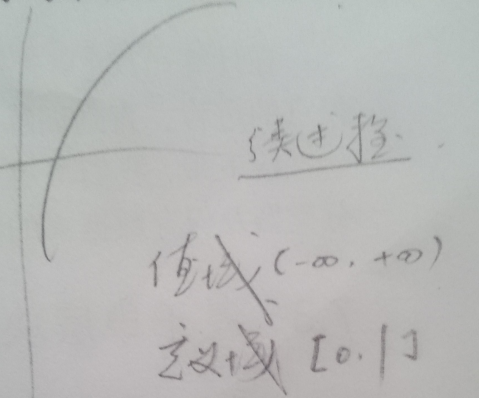
这个图像告诉我们,AdaBoost对后续分类器,给的权是逐渐变大的,因为我们有理由相信,后续分类器更科学一点。
分类器权如何使用呢?假设当前分类器的二类分类结果向量[-1,1,-1,1],那么其加权之后就是$\alpha$ * [-1,1,-1,1]。
对于二类问题,将全部分类器的加权结果累加起来,通过判断加权结果符号的正负判断分类,因为$\alpha$的值域是R,所以只能看符号判断分类。
二、数据权D
每条数据都有权D,该权实际是个概率权,总权和=1。
如果一条数据被正确分类,则$D_{i}^{new}= \frac{D_{i}^{old}*e^{-\alpha}}{Sum(D)}$
如果一条数据被错误分类,则$D_{i}^{new}= \frac{D_{i}^{old}*e^{\alpha}}{Sum(D)}$
正确分类的权会被减小,错误分类的权会被增大。有趣的是,这两个式子如果单从$\alpha$角度来看,似乎有点问题。
如果某次$\alpha$为负,那么$D_{i}^{new}= \frac{D_{i}^{old}*e^{-\alpha}}{Sum(D)}$中$D_{i}^{new}$似乎好像是变大了。
但如果你把$\alpha$的定义式拉到$D_{i}^{new}$里面,就会发现:
$\left\{\begin{matrix}
D_{i}^{new}= \frac{1}{\sqrt{e}}*\frac{1-\varepsilon }{\varepsilon }
\\
D_{i}^{new}= \sqrt{e}*\frac{1-\varepsilon }{\varepsilon}
\end{matrix}\right.$
这样,很明显就可以看出,正确分类的权确实相对于错误分类的权被减小了。
数据权D的引入,主要是采用一种新的方式计算错误率。
一般的错误率$\varepsilon=\frac{errorExamples}{allExamples}$
但是AdaBoost里对错误率也进行加权了,$\varepsilon=\sum_{i=1}^{m}D_{i}*isError?1:0$
由于D是概率权,这样算出来的也算是错误率。如果一条数据分错了、又分错了、还是分错了,那么这条数据理应得到重视,其也会导致错误率比较大。
这种加权错误率对于在单决策树里,从众多变形分类器中,选择一个错误率最低分类器,有很好的参考意义。
③算法过程
★训练过程
while(true)
{
一、构建一个错误率最低的单决策树分类器,并保存记录该分类器全部属性(α、阀值、选取维度、分类结果)
二、利用构建的单决策树分类器计算α加权分类结果
若数据样本分类全部正确(大数据情况下几乎不可能)、分类正确率到达一定情况(多见于正确率收敛)则break
}
★测试过程
for(全部构建的分类器)
for(全部测试数据)
一、使用当前分类器分类
二、累计计算使用全部分类器的加权结果(记录α的原因)
根据加权结果的正负判断分类
不难发现,测试过程其实就是训练过程的某一步提取出来的。
④代码
#include "iostream" #include "fstream" #include "sstream" #include "math.h" #include "vector" #include "string" #include "cstdio" using namespace std; #define fin cin #define inf 1e10 #define D dataSet[0].feature.size() #define delta 100 int sign(double x) {return x<0?-1:1;} struct Data { vector<double> feature; int y; Data(vector<double> feature,int y):feature(feature),y(y) {} }; struct Stump { vector<int> classEst; int dim,symbol; double threshold,error,alpha; Stump() {} Stump(vector<int> classEst,int dim,double threshold,int symbol,double error):classEst(classEst),dim(dim),threshold(threshold),symbol(symbol),error(error) {} }; vector<Data> dataSet; void read() { ifstream fin("traindata.txt"); string line; double fea,cls; int id; while(getline(cin,line)) { vector<double> feature; stringstream sin(line); sin>>id; while(sin>>fea) feature.push_back(fea); cls=feature.back();feature.pop_back(); dataSet.push_back(Data(feature,cls==0?-1:1)); } } vector<int> stumpClassify(int d,double threshold,int symbol) { vector<int> ret(dataSet.size(),1); for(int i=0;i<dataSet.size();i++) { if(!symbol) {if(dataSet[i].feature[d]<=threshold) ret[i]=-1;} else {if(dataSet[i].feature[d]>threshold) ret[i]=-1;} } return ret; } Stump buildStump(vector<double> dataWeight) { int step=10; Stump bestStump; double minError=inf,weightError; for(int i=0;i<D;i++) { double minRange=inf,maxRange=-inf,stepSize; for(int j=0;j<dataSet.size();j++) { minRange=min(minRange,dataSet[j].feature[i]); maxRange=max(maxRange,dataSet[j].feature[i]); } stepSize=(maxRange-minRange)/step; for(int j=0;j<=step;j++) { double threshold=minRange+stepSize*j; for(int k=0;k<=1;k++) { vector<int> classEst=stumpClassify(i,threshold,k); weightError=0.0; for(int t=0;t<classEst.size();t++) if(classEst[t]!=dataSet[t].y) weightError+=dataWeight[t]; if(weightError<minError) { bestStump=Stump(classEst,i,threshold,k,weightError); minError=weightError; } } } } return bestStump; } vector<Stump> mainProcess() { int iter=0,repeat=0,last_cnt=-1; vector<double> dataWeight(dataSet.size(),1.0/dataSet.size()); vector<double> aggClassEst(dataSet.size(),0.0); vector<Stump> stumpList; while(1) { iter++; Stump nowStump=buildStump(dataWeight); double alpha=0.5*log((1.0-nowStump.error)/max(nowStump.error,1e-16)),DSum=0.0; nowStump.alpha=alpha; stumpList.push_back(nowStump); int err_cnt=0; for(int i=0;i<dataSet.size();i++) { double ret=-1*alpha*dataSet[i].y*nowStump.classEst[i]; dataWeight[i]=dataWeight[i]*exp(ret); DSum+=dataWeight[i]; } for(int i=0;i<dataSet.size();i++) { dataWeight[i]/=DSum; aggClassEst[i]+=alpha*nowStump.classEst[i]; if(sign(aggClassEst[i])!=dataSet[i].y) err_cnt++; } //cout<<err_cnt<<"/"<<dataSet.size()<<endl; if(err_cnt!=last_cnt) {last_cnt=err_cnt;repeat=0;} else repeat++; if(err_cnt==0||repeat>delta) break; } return stumpList; } void classify(vector<Stump> stumpList) { ifstream fin("testdata.txt"); dataSet.clear(); string line; double fea,cls; int id; while(getline(cin,line)) { vector<double> feature; stringstream sin(line); sin>>id; while(sin>>fea) feature.push_back(fea); cls=feature.back();feature.pop_back(); dataSet.push_back(Data(feature,cls==0?-1:1)); } vector<double> aggClassEst(dataSet.size(),0.0); for(int i=0;i<stumpList.size();i++) { vector<int> classEst=stumpClassify(stumpList[i].dim,stumpList[i].threshold,stumpList[i].symbol); for(int j=0;j<dataSet.size();j++) aggClassEst[j]+=(stumpList[i].alpha*classEst[j]); } for(int i=0;i<dataSet.size();i++) if(sign(aggClassEst[i])==-1) printf("%test #%d: origin: %d class %d\n",i,dataSet[i].y,-1); else printf("%test #%d: origin: %d class %d\n",i,dataSet[i].y,1); } int main() { read(); vector<Stump> stumpList=mainProcess(); classify(stumpList); }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号