2021icpc南京H（树形dp）

参考题解：
严格鸽
Mercury_City

思路：

根据 \(ti \le 3\) 这个数据范围，我们可以知道蝴蝶最晚消失的时间至少是3秒。
对于一个根节点 \(u\) ,假设其儿子 \(v_1, v_2\) ,我们到达 \(u\) 点之后就会惊动 \(v\) 处的蝴蝶。

当所有儿子的 \(ti < 3\) 时， 我们就在所有儿子中选择一个蝴蝶最多的儿子 \(v_1\) 一路走到底。又因为时间很多，完全可以把所有点走完，所以直接统计就可以了。

当所有儿子的 \(ti = 3\) 时，假设这个节点是 \(v_2\) 。那么我们可以先走 \(v_1\) 拿蝴蝶，之后再回到 \(u\) ，再去 \(v_2\)。这时候就可以分类讨论：

1. \(v_2\) 上的蝴蝶是最大的：

此时就在其他子节点中找到一个最大的先走，然后再走 \(v_2\)

2. \(v_2\) 上的蝴蝶不是最大的：

这时也是在其他节点找一个最大的先走，再走 \(v_2\)

由此，我们可设计状态为 \(f[u]\) 表示：不选 \(u\) 点处蝴蝶（\(u\) 点处蝴蝶飞走了），选从 \(u\) 点出发的所有子节点所得的最大值。

定义 \(sum[u]\) 表示，\(u\) 点的子节点 \(f[v]\) 的和。
画了个图帮助理解：

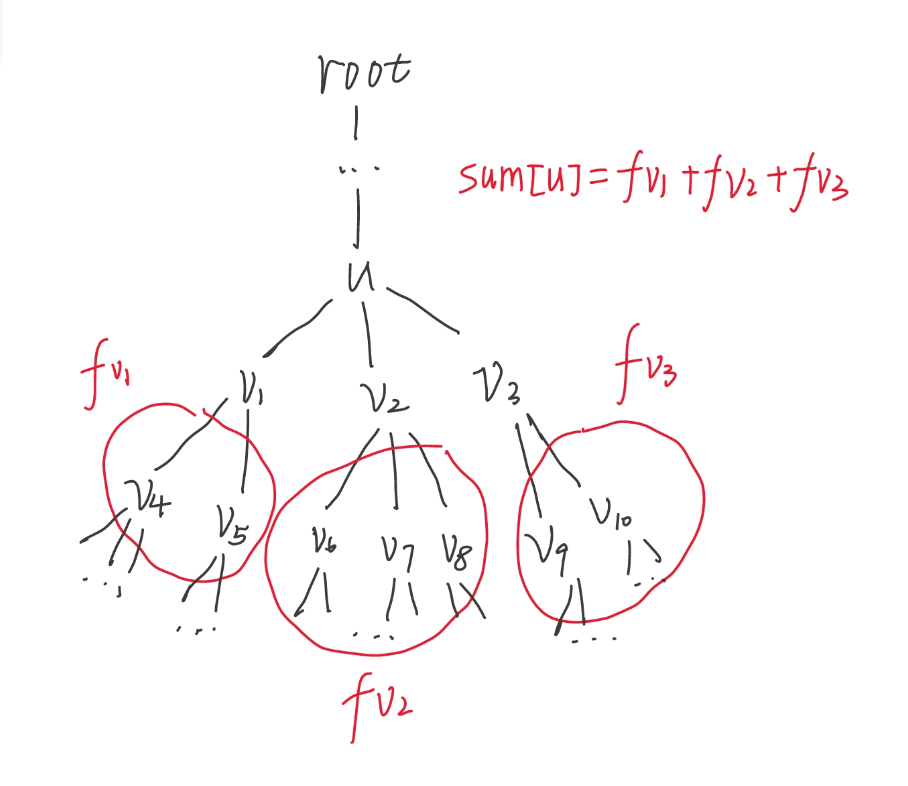
状态转移：

根据上面的分析，我们可得状态转移：

1. \(u\) 的子节点中，\(ti = 3\) 不存在的情况：

   无论我们选哪个子节点，最终的结果都是：\(f[u] = max(f[u]，sum[u] + a[v])\)

2. \(u\) 的子节点中，\(ti = 3\) 存在的情况：

   首先我们先到了点 \(v_1\) ，答案要加上\(a[v_1]\)，拿完之后我们跑去 \(v_2\) 了，此时再加上 \(v_2\) 处的蝴蝶 \(a[v_2]\)。因为我们不往 \(v_1\) 下面走了，而此时 \(v_1\) 的子节点也被惊动了，肯定会飞走，可以表示为表示为 \(sum[u] - f[v_1]\) 。又因为时间无限多，我们以后可能还会往 \(v_1\) 的 子节点 的 子节点 走，所以要再加上 \(sum[v_1]\) 。最终的方程就是：\(f[u] = max(f[u], sum[u] - f[v_1] + a[v_1]+a[v_2] + sum[v_1])\)

代码：

#include<bits/stdc++.h>

#define int long long
using namespace std;
#define fi first
#define se second
#define cf int T;cin >> T;while (T --)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);

typedef pair<int, int> pii;
const int N = 2e5 + 10, mod = 998244353, inf = 0x3f3f3f3f;
int dp[N];
int sum[N], t[N];
int a[N];
vector<int> g[N];
int n, u, v;

void dfs(int u, int fa) {
	int mx = 0;
	for (auto v: g[u]) {
		if (v == fa) continue;
		dfs(v, u);
		sum[u] += dp[v];
		mx = max(mx, a[v]);
	}
	dp[u] = sum[u] + mx;
	
	mx = 0;
	int idx = 0;
	for (auto v: g[u]) {
		if (v == fa) continue;
		if (t[v] == 3 && a[v] > mx)
			mx = a[v], idx = v;
	}
	int minn = - inf * inf;
	for (auto v: g[u]) {
		if (v == fa) continue;
		if (v != idx)
			minn = max(minn, sum[v] + a[v] - dp[v]);
	}
	dp[u] = max(dp[u], sum[u] + mx + minn);
	
	mx = 0, idx = 0;
	minn = - inf * inf;
	for (auto v: g[u]) {
		if (v == fa) continue;
		if (sum[v] + a[v] - dp[v] > minn)
			minn = sum[v] + a[v] - dp[v], idx = v;
	}
	
	for (auto v: g[u]) {
		if (v == fa) continue;
		if (v != idx && t[v] == 3)
			mx = max(mx, a[v]);
	}
	dp[u] = max(dp[u], sum[u] + mx + minn);
}

void solve() {
	cin >> n;
	for (int i = 1; i <= n; i ++) {
		g[i].clear();
		dp[i] = sum[i] = 0;
	}
	for (int i = 1; i <= n; i ++) cin >> a[i];
	for (int i = 1; i <= n; i ++) cin >> t[i];
	for (int i = 1; i <= n - 1; i ++) {
		cin >> u >> v;
		g[u].push_back(v);
		g[v].push_back(u);
	}
	dfs(1, 0);
	cout << dp[1] + a[1] << endl;
}

signed main() {
#ifndef ONLINE_JUDGE
	freopen("cin.in", "r", stdin);
	freopen("cout.out", "w", stdout);
#endif
	IOS
	cf solve();
	return 0;
}