BZOJ 4823: [Cqoi2017]老C的方块




分析:
我觉得我的网络流白学了...QAQ...
其实数据范围本是无法用网络流跑过去的,然而出题者想让他跑过去,也就跑过去了...
看到题目其实感觉很麻烦,不知道从哪里入手,那么仔细观察所给出的有用信息...
我们考虑网格图是一个含有挡板的图,这个挡板的分布很有规律,大概是每一行的相邻两个挡板都隔了四个格子,并且奇数行的排列相同,偶数行的排列相同...
然后考虑不合法的方块形状有什么共同点:仔细观察就会发现,所有的不合法图形中,挡板的左边至少有一个格子,右边至少有一个格子,并且左边的格子连着一个格子,右边的的格子连着一个格子...也就是说,其实我们如果要使得整张图的所有方块构成的图形全部合法就要满足下图中如果挡板两边的紫色格子都有方块存放的话,那么,和这两个紫色格子相邻的色格子和黑色格子不能同时存在...

我们发现刚好相邻隔板之间的四个格子就是为不合法图案而设计的...
于是就变成了经典的限制问题...经典的最小割...
如果不考虑紫色的格子,那么这整张网格图就是一个二分图...我们给这张图染色...
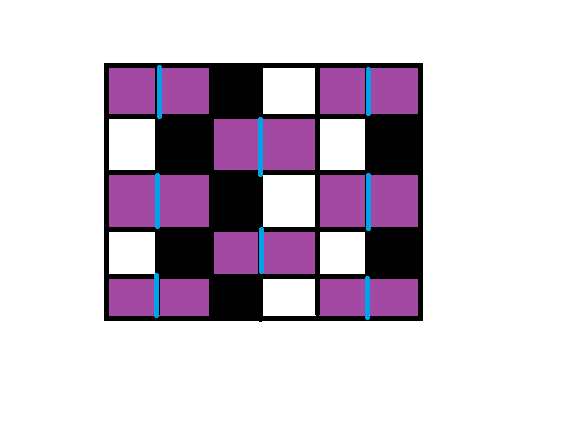
那么对于所有的白点,我们连$<S,x,w[x]>$的边,对于所有的黑点我们连$<x,T,w[x]>$的边,然后因为要保证紫色格子周围黑白点不能同时存在,所以,对于所有的黑点,我们从紫色格子像黑点连$inf$的边,从白点像紫色格子连$inf$的边,然后因为我们两个紫色格子不同时存在的时候黑白点是可以同时存在的,所以两个紫色格子之间连上$min(w[x],w[y])$的边...然后求最小割就好了...
给出了不合法的图形,一定要找到不合法的方案的相同点,然后转换成一些基础的模型来解决...
对于网格图的问题,二分图应该是最常见的应用...
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<map>
//by NeighThorn
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=100000+5,maxm=1000000+5;
int n,m,S,T,no,cnt;
int hd[maxn],fl[maxm],to[maxm],nxt[maxm],pos[maxn];
int mv[2][3][2]={-1,0,1,0,0,1,-1,0,1,0,0,-1};
vector<int> v[maxn];
map< pair<int,int>,pair<int,int> > mp;
inline void add(int x,int y,int s){
fl[cnt]=s;to[cnt]=y;nxt[cnt]=hd[x];hd[x]=cnt++;
fl[cnt]=0;to[cnt]=x;nxt[cnt]=hd[y];hd[y]=cnt++;
}
inline bool bfs(void){
memset(pos,-1,sizeof(pos));
int head=0,tail=0,q[maxn];
q[0]=S;pos[S]=0;
while(head<=tail){
int top=q[head++];
for(int i=hd[top];i!=-1;i=nxt[i])
if(fl[i]&&pos[to[i]]==-1)
pos[to[i]]=pos[top]+1,q[++tail]=to[i];
}
return pos[T]!=-1;
}
inline int find(int v,int f){
if(v==T) return f;
int res=0,t;
for(int i=hd[v];i!=-1&&f>res;i=nxt[i])
if(pos[to[i]]==pos[v]+1&&fl[i])
t=find(to[i],min(f-res,fl[i])),res+=t,fl[i]-=t,fl[i^1]+=t;
if(!res) pos[v]=-1;
return res;
}
inline int dinic(void){
int res=0,t;
while(bfs())
while(t=find(S,inf))
res+=t;
return res;
}
signed main(void){
#ifndef ONLINE_JUDGE
freopen("block1.in","r",stdin);
#endif
memset(hd,-1,sizeof(hd));
scanf("%d%d%d",&m,&n,&no);S=0,T=no+1;
for(int i=1,x,y,w;i<=no;i++)
scanf("%d%d%d",&y,&x,&w),mp[make_pair(x,y)]=make_pair(i,w),v[x].push_back(y);
for(int i=1;i<=n;i++)
sort(v[i].begin(),v[i].end());
for(int i=1,x,y,xw,yw,be,lx,ly,rx,ry;i<=n;i++)
for(int j=0;j<v[i].size();j++){
x=i,y=v[i][j];
if((x&1)&&y%4==1){
if(j<v[i].size()-1&&v[i][j+1]==y+1)
add(mp[make_pair(x,y)].first,mp[make_pair(x,y+1)].first,min(mp[make_pair(x,y)].second,mp[make_pair(x,y+1)].second));
}
else if((x&1)&&y%4==2){
for(int k=0;k<3;k++)
if(mp.find(make_pair(x+mv[0][k][0],y+mv[0][k][1]))!=mp.end())
add(mp[make_pair(x,y)].first,mp[make_pair(x+mv[0][k][0],y+mv[0][k][1])].first,inf);
}
else if((x&1)==0&&y%4==0){
if(j>0&&v[i][j-1]==y-1)
add(mp[make_pair(x,y)].first,mp[make_pair(x,y-1)].first,min(mp[make_pair(x,y)].second,mp[make_pair(x,y-1)].second));
}
else if((x&1)==0&&y%4==3){
for(int k=0;k<3;k++)
if(mp.find(make_pair(x+mv[1][k][0],y+mv[1][k][1]))!=mp.end())
add(mp[make_pair(x,y)].first,mp[make_pair(x+mv[1][k][0],y+mv[1][k][1])].first,inf);
}
else if(((x+y)&1)&&(x&1)){
for(int k=0;k<3;k++)
if(mp.find(make_pair(x+mv[0][k][0],y+mv[0][k][1]))!=mp.end())
add(mp[make_pair(x,y)].first,mp[make_pair(x+mv[0][k][0],y+mv[0][k][1])].first,inf);
add(S,mp[make_pair(x,y)].first,mp[make_pair(x,y)].second);
}
else if((x&1)&&((x+y)&1)==0){
for(int k=0;k<3;k++)
if(mp.find(make_pair(x+mv[1][k][0],y+mv[1][k][1]))!=mp.end())
add(mp[make_pair(x+mv[1][k][0],y+mv[1][k][1])].first,mp[make_pair(x,y)].first,inf);
add(mp[make_pair(x,y)].first,T,mp[make_pair(x,y)].second);
}
else if(((x+y)&1)&&(x&1)==0){
for(int k=0;k<3;k++)
if(mp.find(make_pair(x+mv[1][k][0],y+mv[1][k][1]))!=mp.end())
add(mp[make_pair(x,y)].first,mp[make_pair(x+mv[1][k][0],y+mv[1][k][1])].first,inf);
add(S,mp[make_pair(x,y)].first,mp[make_pair(x,y)].second);
}
else{
for(int k=0;k<3;k++)
if(mp.find(make_pair(x+mv[0][k][0],y+mv[0][k][1]))!=mp.end())
add(mp[make_pair(x+mv[0][k][0],y+mv[0][k][1])].first,mp[make_pair(x,y)].first,inf);
add(mp[make_pair(x,y)].first,T,mp[make_pair(x,y)].second);
}
}
printf("%d\n",dinic());
return 0;
}
By NeighThorn


 浙公网安备 33010602011771号
浙公网安备 33010602011771号