二叉树链式存储 - C语言 - 【大话数据结构】

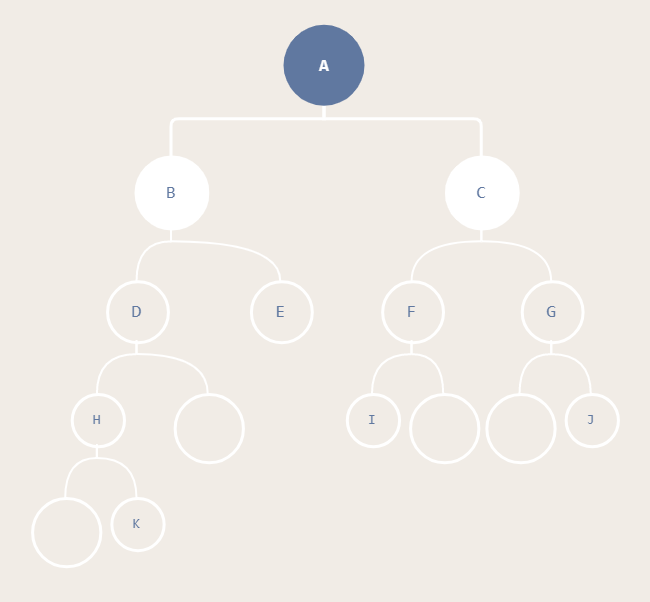
前序遍历二叉树:ABDHKECFIGJ
中序遍历二叉树:HKDBEAIFCGJ
后序遍历二叉树:KHDEBIFJGCA

// 二叉树的链式存储
#include "stdlib.h"
#include "stdio.h"
#include "io.h"  
#include "string.h"
#include "math.h"

#define Nil '#'
#define ARRAY_MAXSIZE 30
#define TRUE 1
#define FALSE 0

typedef char TElemType;
//int index = 1;
//typedef char String[24]; /*  0号单元存放串的长度 */
//String str;
// 定义数据结构
typedef struct node
{
	TElemType data; // 存储的数据类型，使用别名TElemType【类型泛化】
	struct node*lchild, *rchild; // 定义左右子树
}BiNode, *BiTree;
int index = 1;
// 定义字符串
typedef struct
{
	char charArray[ARRAY_MAXSIZE];
}String;


///* *****通用函数***** */

void initialString(String *s, const char *chars)
{
	if (strlen(chars) > ARRAY_MAXSIZE)
		printf("字符溢出（字符串长度超过规定的最大长度:%d\n）", ARRAY_MAXSIZE);
	else
	{
		s->charArray[0] = strlen(chars);
		for (int i = 1; i <= s->charArray[0]; i++)
		{
			s->charArray[i] = *(chars +(i-1)); // 指针索引关系
		}
	}
}

void println(TElemType e)
{
	printf(" %c ", e);
}

int isEmpty(BiTree T)
{
	if (T) // T!=NULL, 即T不空
		return FALSE;
	else
		return TRUE;
}

// 每递归一层，深度加1
int depth(BiTree T)
{
	int l, r;
	if (!T) 
	{
		return 0;
	}
	else 
	{
		l = depth(T->lchild);
		r = depth(T->rchild);
	}
	int depth = (l > r ? l + 1 : r + 1);
	return depth;
}

TElemType root(BiTree T)
{
	if (T)
		return ' ';
	else
	{
		return T->data;
	}
}

/* *****通用函数***** */


void initBiTree(BiTree *T)
{
	*T = NULL;
}

void destroyBiTree(BiTree* T)
{
	if (*T)
	{
		if ((*T)->lchild)
			destroyBiTree(&(*T)->lchild);
		if ((*T)->rchild)
			destroyBiTree(&(*T)->rchild);
		free(*T); // 释放根结点
		*T = NULL; // 空指针赋值0
	}
}

#define clearBiTree destroyBiTree  

// - 创建二叉树
// - 结点分类两种：
//		1 空节点'#'
//		2 字符结点
// - 创建二叉树有两种方式：
//		1 通过有序字符串创建二叉树
//		2 用户输入创建二叉树
void createBiTree(BiTree* T, String str)
{
	TElemType ch;
	ch = str.charArray[index++];

	if (ch == Nil)
		*T = NULL;
	else 
	{
		*T = (BiTree)malloc(sizeof(BiNode));
		if (!*T)
			exit(OVERFLOW);
		(*T)->data = ch; /* 生成根结点 */
		createBiTree(&(*T)->lchild, str); /* 构造左子树 */
		createBiTree(&(*T)->rchild, str); /* 构造右子树 */
	}
}

/* 初始条件: 二叉树T存在 */
/* 操作结果: 前序递归遍历T */
void preOrderTraverse(BiTree T)
{
	if (T == NULL)
		return;
	printf("%c", T->data);/* 显示结点数据，可以更改为其它对结点操作 */
	preOrderTraverse(T->lchild); /* 再先序遍历左子树 */
	preOrderTraverse(T->rchild); /* 最后先序遍历右子树 */
}

/* 初始条件: 二叉树T存在 */
/* 操作结果: 中序递归遍历T */
void inOrderTraverse(BiTree T)
{
	if (T == NULL)
		return;
	inOrderTraverse(T->lchild); /* 中序遍历左子树 */
	printf("%c", T->data);/* 显示结点数据，可以更改为其它对结点操作 */
	inOrderTraverse(T->rchild); /* 最后中序遍历右子树 */
}

/* 初始条件: 二叉树T存在 */
/* 操作结果: 后序递归遍历T */
void postOrderTraverse(BiTree T)
{
	if (T == NULL)
		return;
	postOrderTraverse(T->lchild); /* 先后序遍历左子树  */
	postOrderTraverse(T->rchild); /* 再后序遍历右子树  */
	printf("%c", T->data);/* 显示结点数据，可以更改为其它对结点操作 */
}



int main()
{
	BiTree T;
	TElemType e;
	initBiTree(&T);

	String str;
	initialString(&str, "ABDH#K###E##CFI###G#J##");

	createBiTree(&T, str);

	printf("构造空二叉树后,树空否？%d(1:是 0:否) 树的深度=%d\n", isEmpty(T), depth(T));

	e = root(T);
	printf("二叉树的根为: %c\n", e);


	printf("\n前序遍历：");
	preOrderTraverse(T);
	printf("\n中序遍历：");
	inOrderTraverse(T);
	printf("\n后序遍历：");
	postOrderTraverse(T);

	clearBiTree(&T);
	printf("\n清除二叉树后,树空否？%d(1:是 0:否) 树的深度=%d\n", isEmpty(T), depth(T));
}