图解leetcode —— 128. 最长连续序列
前言:
每道题附带动态示意图,提供java、python两种语言答案,力求提供leetcode最优解。
描述:
给定一个未排序的整数数组,找出最长连续序列的长度。
要求算法的时间复杂度为 O(n)。
示例:
输入: [100, 4, 200, 1, 3, 2]
输出: 4
解释: 最长连续序列是 [1, 2, 3, 4]。它的长度为 4。
思路:
首先,我们先来看一个简单的例子:序列123 序列 56,插入4,求连续序列长度。
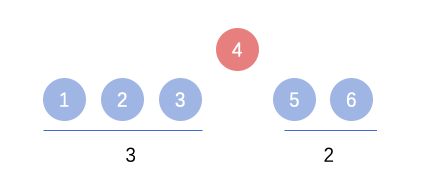
很容易得出结论,答案是6,那么这个6是怎么来的呢?6 = len(1,2,3) + len(5,6) + 1。
当4插入的时候,我们关心的是3,5,而当序列1,2,3,4,5,6一旦形成,那么元素2,3,4,5我们将不会关心,因为无论新加入序列的元素取何值,都不会和元素2,3,4,5组合成连续序列。
那么我们是否可以将连续序列的长度,当作一种状态,绑定在连续序列的首尾元素上?
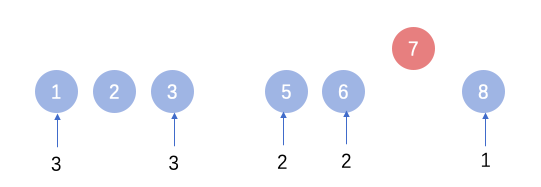
此时,当元素7插入序列后,组成的最大连续序列就是4 = 2+1+1,因此我们可以分析出,该问题的dp方程是 dp[i] = dp[i - 1] + dp[i+1]
我们可以借助散列表来简化时间复杂度。
图解:
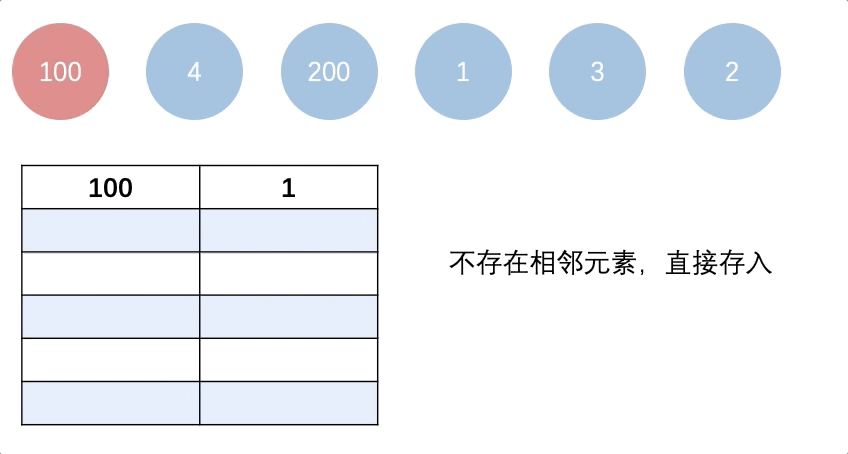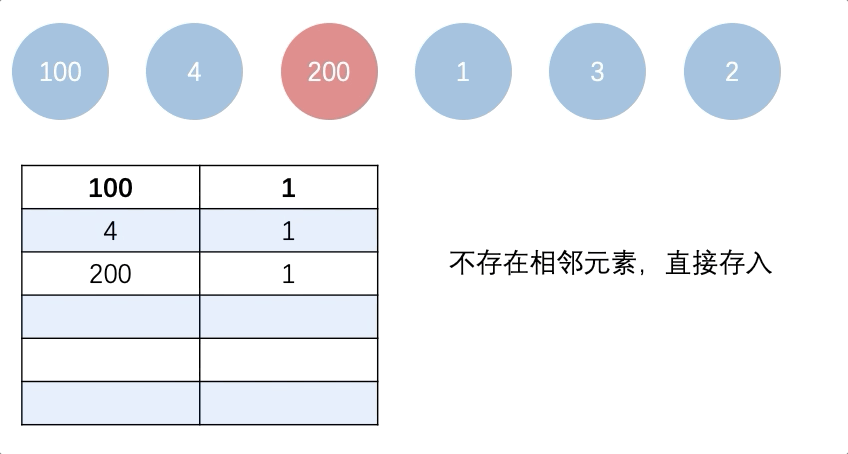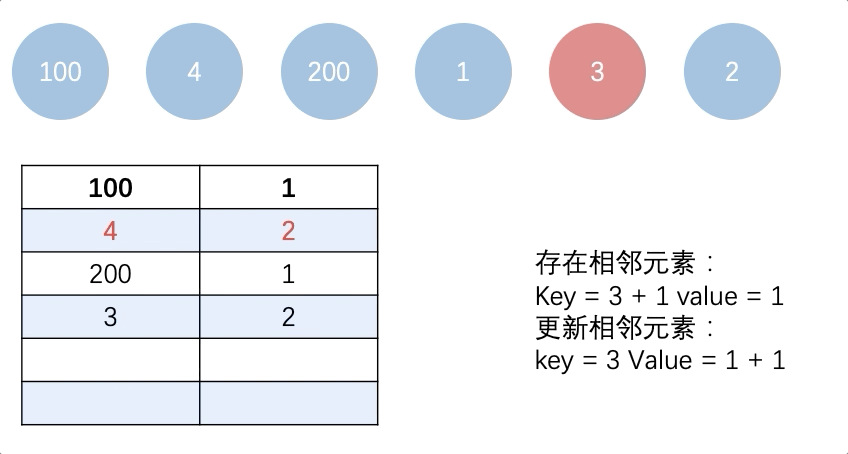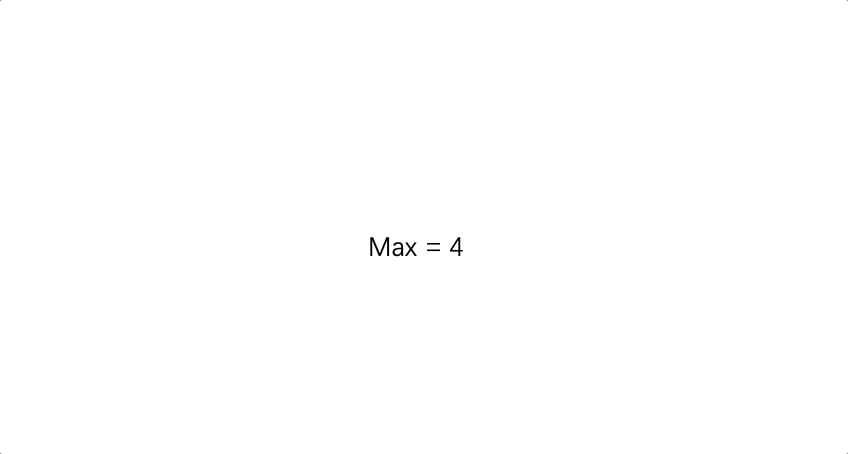
java:
class Solution { public int longestConsecutive(int[] nums) { int len = nums.length; int max = 0; if (len == 0) { return max; } HashMap<Integer, Integer> map = new HashMap<>(len); for (int i = 0; i < len; i++) { if (!map.keySet().contains(nums[i])) { Integer before = map.getOrDefault(nums[i] - 1, 0); Integer after = map.getOrDefault(nums[i] + 1, 0); int value = before + after + 1; max = Math.max(value, max); map.put(nums[i] - before, value); map.put(nums[i] + after, value); } } return max; } }
结果:
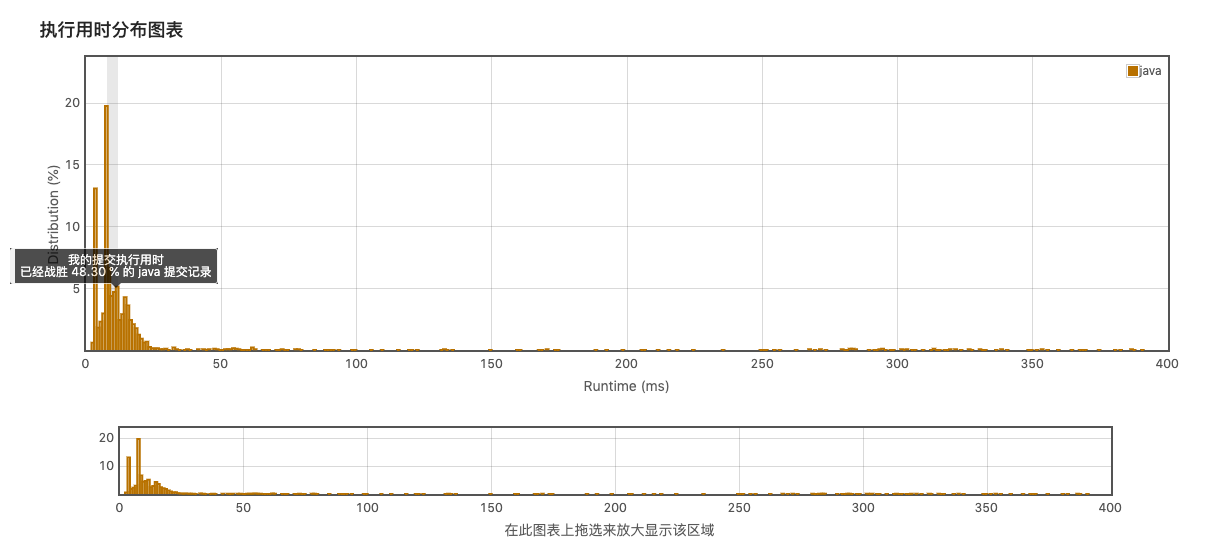
python:
class Solution(object): def longestConsecutive(self, nums): hash_dict = dict() max_length = 0 for num in nums: if num not in hash_dict: left = hash_dict.get(num - 1, 0) right = hash_dict.get(num + 1, 0) cur_length = 1 + left + right if cur_length > max_length: max_length = cur_length hash_dict[num] = cur_length hash_dict[num - left] = cur_length hash_dict[num + right] = cur_length return max_length
结果:
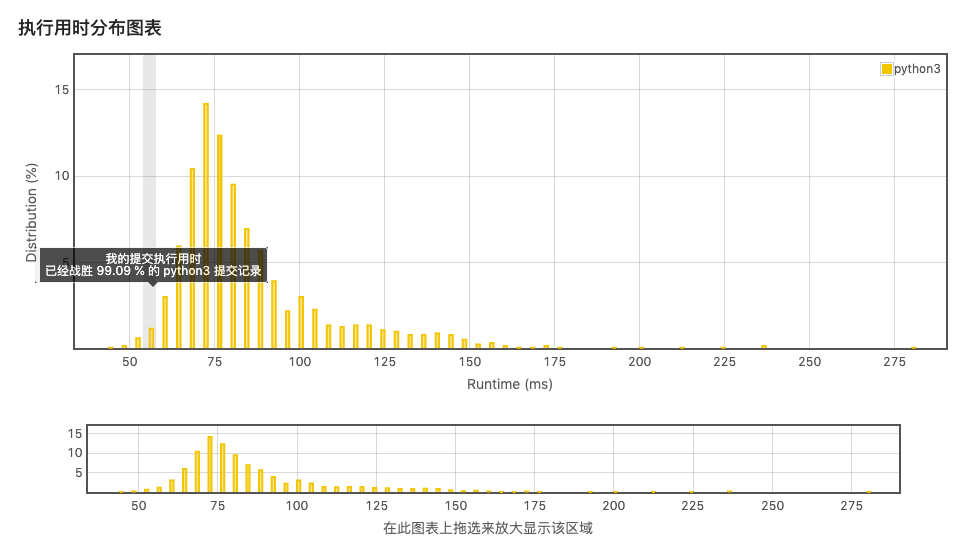


 浙公网安备 33010602011771号
浙公网安备 33010602011771号