区域和检索 - 数组不可变
描述:
给定一个整数数组 nums,求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和,包含 i, j 两点。
示例:
给定 nums = [-2, 0, 3, -5, 2, -1],求和函数为 sumRange()
sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3
说明:
你可以假设数组不可变。
会多次调用 sumRange 方法。
思路:
这道题可以用动态规划的思想来解决,即sumRange(i, j) = dp[j] - dp[i],dp数组为当前位置的sums和。
可以类比为:有A、B、C三个点依次在一条直线上,求dist(B,C) = dist(A,C) -dist(A,B)
java:
class NumArray { private int[] sum; public NumArray(int[] nums) { sum = new int[nums.length + 1]; for (int i = 0; i < nums.length; i++) { sum[i + 1] = nums[i] + sum[i]; } } public int sumRange(int i, int j) { return sum[j + 1] - sum[i]; } }
结果:
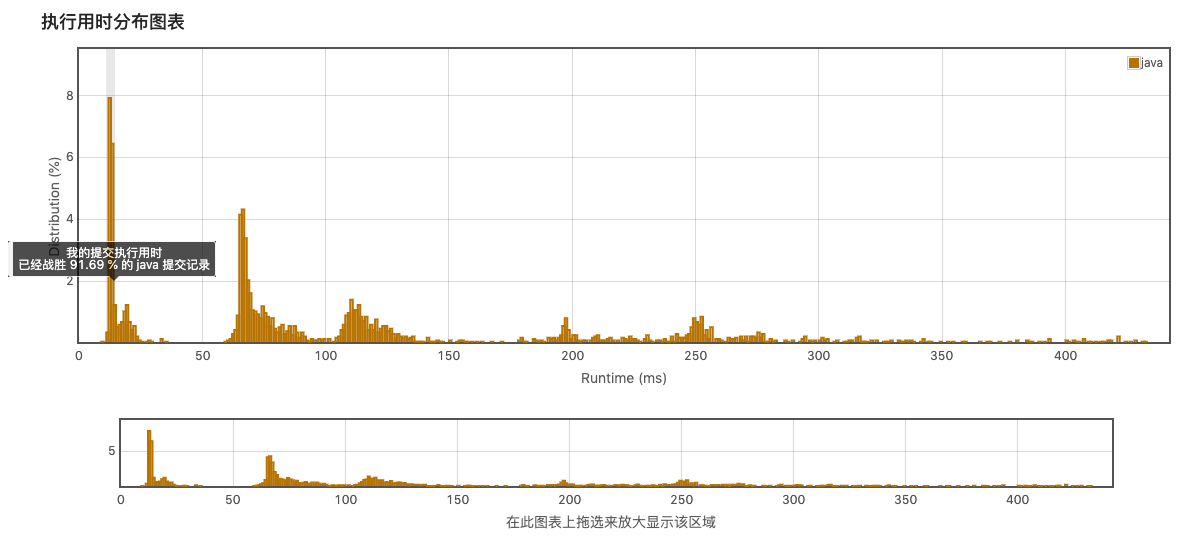
python:
class NumArray: def __init__(self, nums: List[int]): self.dp = nums[:] self.dp.insert(0, 0) for i in range(0, len(nums)): self.dp[i + 1] = nums[i] + self.dp[i] def sumRange(self, i: int, j: int) -> int: return self.dp[j + 1] - self.dp[i]
结果:
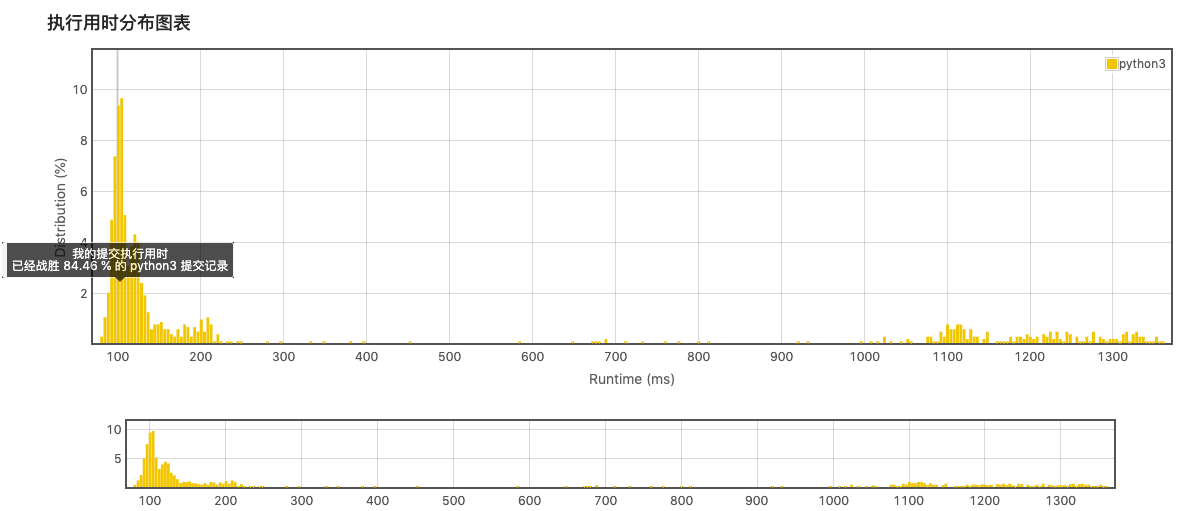



 浙公网安备 33010602011771号
浙公网安备 33010602011771号