理解常见优化算法

梯度下降法

梯度：梯度是矢量，设函数\(f(x_0,x_1,\cdots,x_n)\)在空间中有一阶连续偏导数，对空间中的点\(P(a_0,a_1,\cdots,a_n)\)有向量\(\vec{g}=(\frac{\partial f}{\partial a_0},\frac{\partial f}{\partial a_2},\cdots,\frac{\partial f}{\partial a_n})\)，\(\vec{g}\)即为\(P\)的梯度，\(\nabla_{\vec{a}} f=\nabla f(a_0,a_1,\cdots,a_n)=\vec{g}\)。

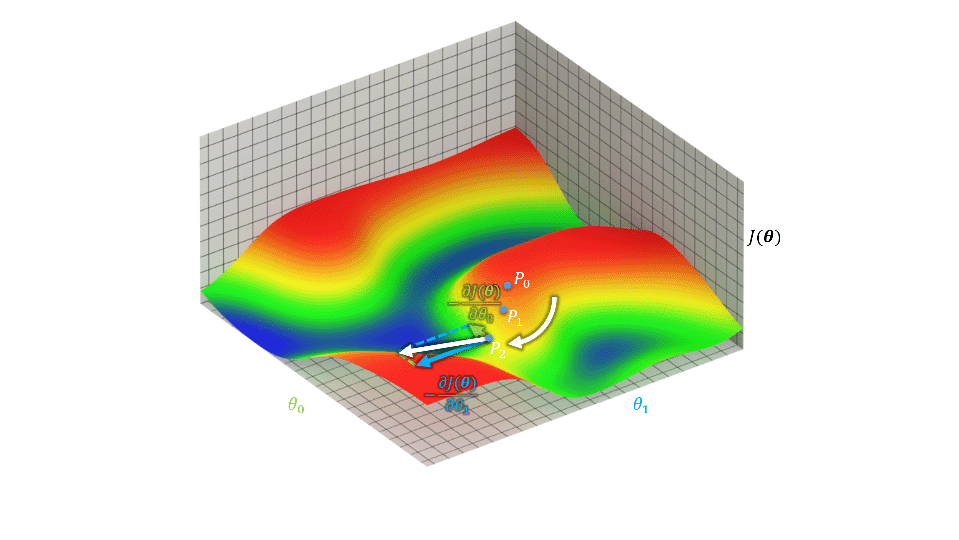
梯度下降法对参数对初值敏感，参数初值的不同可能得到不同结果，下图中\(P_0\)位置略微改变就会收敛到右侧蓝色区域中。

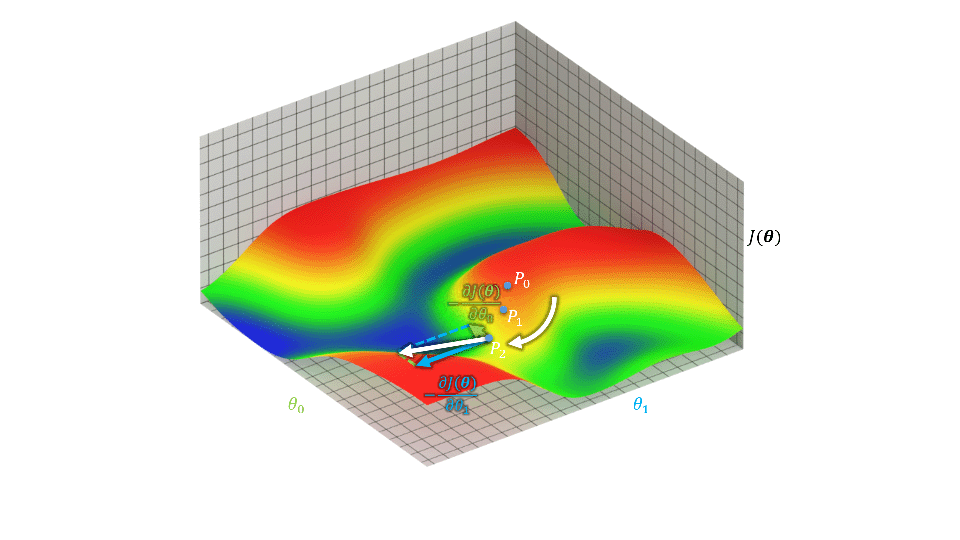
计算输出\(\hat{y}=f_\boldsymbol{\theta}(\boldsymbol{X})=\sum_{i=0}^{n}\theta_i x_i=\boldsymbol{\theta}^T\boldsymbol{X}\)，其中\(\boldsymbol{\theta}\)为参数，\(\boldsymbol{X}=\begin{bmatrix} x_0 & x_1 & \cdots & x_n \end{bmatrix}^T\)，\(\boldsymbol{\theta}=\begin{bmatrix} \theta_0 & \theta_1 & \cdots & \theta_n \end{bmatrix}^T\)。

损失函数\(J(\boldsymbol{\theta})={\frac{1}{2}\sum_{j=0}^m(y_j-\hat{y}_j)^2}\)描述了输出与目标之间的差距。欲使这个差距充分小，即求\(\min_\theta{J(\boldsymbol{\theta})}\)，可以通过\(\theta_i^{new}=\theta_i+Lr\nabla_{\theta_i}J=\theta_i+Lr\frac{\partial J(\boldsymbol{\theta})}{\partial\theta_i}=\theta_i+Lr\sum_{j=0}^m(y_j-\hat{y}_j)\frac{\partial \sum_{j=0}^m(y_j-f_\boldsymbol{\theta}(\boldsymbol{X}_j))}{\partial\theta_i}=\theta_i+Lr\sum_{j=0}^m(y_j-\hat{y}_j)x_i\)多次迭代做到，即\(\boldsymbol{\theta}^{new}=\boldsymbol{\theta}+Lr\nabla_\boldsymbol{\theta}J\)。其中\(Lr\)为学习率，\(i\)为样本中的属性序号，\(j\)为样本序号。当这个差距充分小时可以视为取得局部最优。

随机梯度下降法

对于训练集很大的情况，采用：\(\theta_i^{new}=\theta_i-Lr(y_j-\hat{y}_j)x_i\)，遍历\(i\)和\(j\)来更新参数，即每次更新参数仅使用一个样本。这样可以减少运算量但会使得计算结果接近但难以达到最优。

牛顿法

泰勒中值定理：
当函数\(h(\theta)\)在\(\theta_0\)处具有\(n\)阶导数时，在\(\theta_0\)的邻域\(U(\theta_0)\)内恒有：

\[h(\theta)=\sum_{i=0}^n \frac{h^{(i)}(\theta_0)}{i!}(\theta-\theta_0)^i+R_n(\theta) \]

由定理得：\(h(\theta)\)在\(\theta_0\)处具有一阶导数时有：\(h(\theta)=h(\theta_0)+h^\prime(\theta_0)(\theta-\theta_0)+lost\)，它的根\(\theta=\theta_0-\frac{h(\theta_0)}{h^\prime(\theta_0)}-lost\)，其中\(lost\)为损失。欲使损失充分小，则可以通过\(\theta_{n+1}=\theta_n-\frac{h(\theta_n)}{h^\prime(\theta_n)}\)多次迭代来做到。这个公式中的下标描述当前值为第几次迭代的结果。

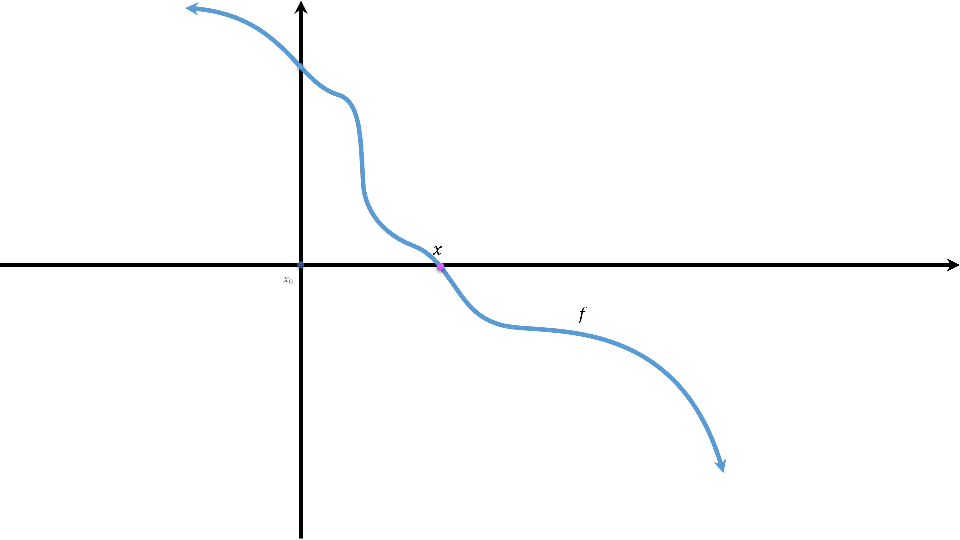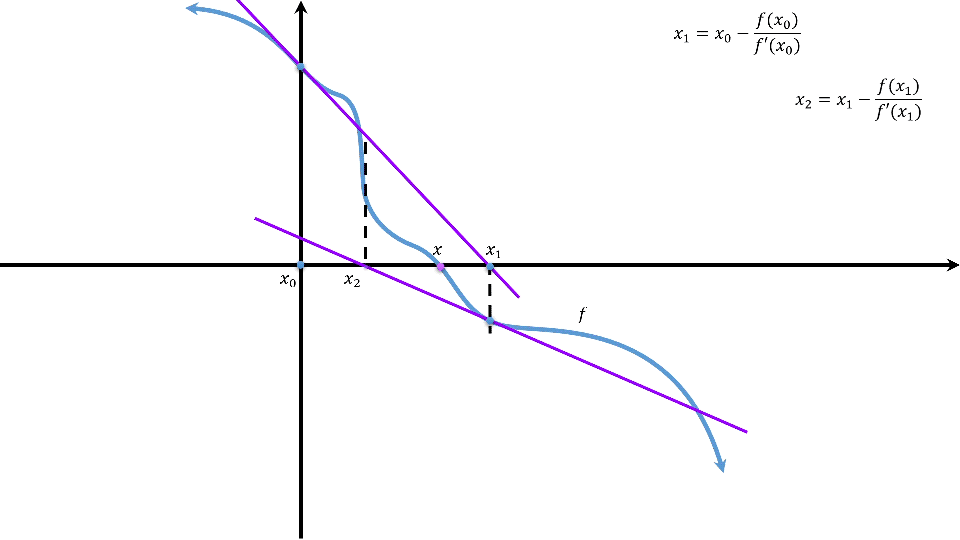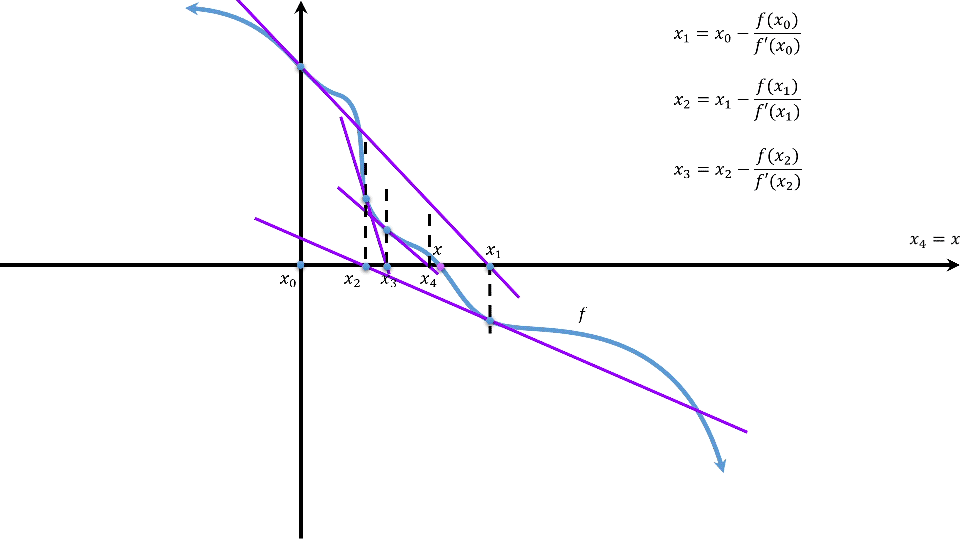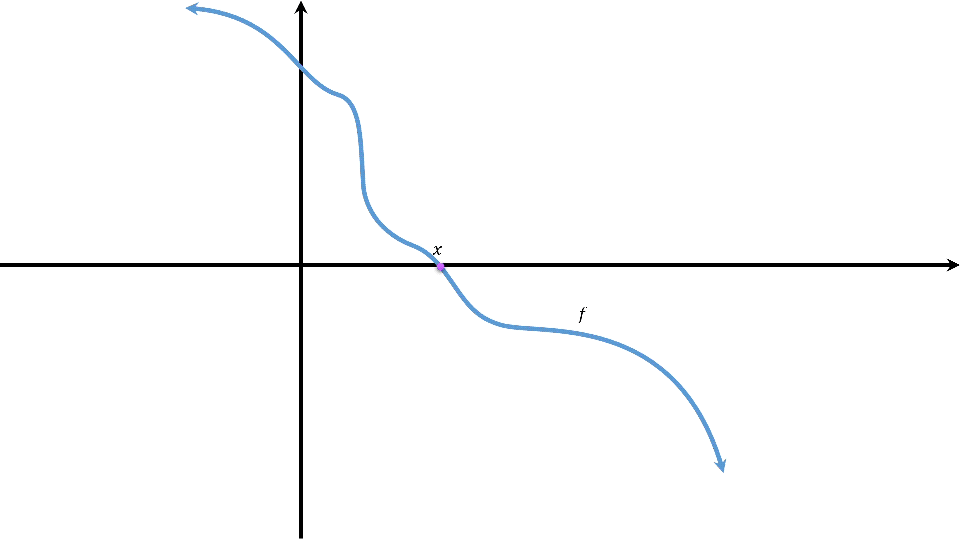
海塞矩阵：当\(n\)元实函数\(f(x_0,x_1,\cdots,x_n)\)在点\(P(\hat{x}_0,\hat{x}_1,\cdots,\hat{x}_n)\)处有二阶偏导，则\(f\)在\(P\)处的海塞矩阵为：

\[\boldsymbol{H}=\begin{bmatrix} \frac{\partial^2f}{\partial \hat{x}_1\partial \hat{x}_1} & \frac{\partial^2f}{\partial \hat{x}_1\partial \hat{x}_2} & \cdots & \frac{\partial^2f}{\partial \hat{x}_1\partial \hat{x}_n} \\ \frac{\partial^2f}{\partial \hat{x}_2\partial \hat{x}_1} & \frac{\partial^2f}{\partial \hat{x}_2\partial \hat{x}_2} & \cdots & \frac{\partial^2f}{\partial \hat{x}_2\partial \hat{x}_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2f}{\partial \hat{x}_n\partial \hat{x}_1} & \frac{\partial^2f}{\partial \hat{x}_n\partial \hat{x}_2} & \cdots & \frac{\partial^2f}{\partial \hat{x}_n\partial \hat{x}_n} \end{bmatrix} \]

由定理得：\(h(\boldsymbol{\theta})\)在\(\boldsymbol{\theta}_0\)处具有二阶导数时，它的根\(\boldsymbol{\theta}=\begin{bmatrix} \theta_0 & \theta_1 & \cdots & \theta_n \end{bmatrix}^T=\boldsymbol{\theta}_0-\boldsymbol{H}^{-1}\nabla h(\boldsymbol{\theta}_0)-lost\)，其中\(lost\)为损失。欲使损失充分小，则可以通过\(\boldsymbol{\theta}^{new}=\boldsymbol{\theta}-\boldsymbol{H}^{-1}\nabla h(\boldsymbol{\theta})\)多次迭代来做到。同理求\(\hat{y}=h(\boldsymbol{\theta})\)使\(\hat{y}\rightarrow y\)。但是每次迭代求海塞矩阵的逆\(\boldsymbol{H}^{-1}\)却比较困难。

矩阵的逆：\(\boldsymbol{AB}=\boldsymbol{BA}=\boldsymbol{E}\)则\(\boldsymbol{A}=\boldsymbol{B}^{-1}\)、\(\boldsymbol{B}=\boldsymbol{A}^{-1}\)，\(\boldsymbol{A}\)、\(\boldsymbol{B}\)互为逆矩阵。

拟牛顿法

尝试近似求取海塞矩阵。在\(\boldsymbol{\theta}_{k+1}=\boldsymbol{\theta}_{k}-\boldsymbol{G}_{k}^{-1}\nabla h(\boldsymbol{\theta}_{k})\)中，下标描述当前值为第几次迭代的结果，不要纠结\(\boldsymbol{G}\)是怎么回事，它只是换了一个字母来表示。拟牛顿法试图确定\(\boldsymbol{H}_{k+1}=\boldsymbol{H}_k+\Delta\boldsymbol{H}_k\)使得\(\boldsymbol{H}_{k+1}\approx \boldsymbol{G}_{k+1}^{-1}\)，这样一来就有\(\boldsymbol{\theta}_{k+1}=\boldsymbol{\theta}_{k}-\boldsymbol{H}_{k}\nabla h(\boldsymbol{\theta}_{k})\)。

拟牛顿方程：\(\boldsymbol{H}_{k+1}\boldsymbol{y}_k\approx\boldsymbol{s}_k\)，其中\(\boldsymbol{s}_k=\boldsymbol{\theta}_{k+1}-\boldsymbol{\theta}_k\)、\(\boldsymbol{y}_k=\nabla h(\boldsymbol{\theta}_{k+1})-\nabla h(\boldsymbol{\theta}_{k})\)。

有了拟牛顿方程，可以确定校正矩阵\(\Delta\boldsymbol{H}_k\)了。

算法	提出年份	\(\Delta\boldsymbol{H}_k\)
DFP算法	1959	\(\displaystyle\Delta\boldsymbol{H}_k=-\frac{\boldsymbol{H}_k\boldsymbol{y}_k\boldsymbol{y}_k^T\boldsymbol{H}_k}{\boldsymbol{y}_k^T\boldsymbol{H}_k\boldsymbol{y}_k}+\frac{\boldsymbol{s}_k\boldsymbol{s}_k^T}{\boldsymbol{y}_k^T\boldsymbol{s}_k}\)
Broyden族 拟牛顿算法	1967	\(\displaystyle\Delta\boldsymbol{H}_k=-\frac{\boldsymbol{H}_k\boldsymbol{y}_k\boldsymbol{y}_k^T\boldsymbol{H}_k}{\boldsymbol{y}_k^T\boldsymbol{H}_k\boldsymbol{y}_k}+\frac{\boldsymbol{s}_k\boldsymbol{s}_k^T}{\boldsymbol{y}_k^T\boldsymbol{s}_k}+\phi \boldsymbol{w}_k\boldsymbol{w}_k^T,\\\phi \in \mathbb{R},\boldsymbol{w}_k=(\boldsymbol{y}_k^T\boldsymbol{H}_k\boldsymbol{y}_k)^\frac{1}{2}(\frac{\boldsymbol{s}_k}{\boldsymbol{y}_k^T\boldsymbol{s}_k}-\frac{\boldsymbol{H}_k\boldsymbol{y}_k}{\boldsymbol{y}_k^T\boldsymbol{H}_k\boldsymbol{y}_k})\)
BFGS算法	1970	Broyden族拟牛顿算法，令\(\phi=1\)

BFGS算法是很有效的拟牛顿法。

EM算法（最大期望算法）

设随机事件\(A=\{a_1,a_2,\cdots,a_i,\cdots,a_n\}\)、\(B=\{b_1,b_2,\cdots,b_m\}\)：

• \(P(a_i)\)表示\(A=a_i\)的概率。
• \(P(A\cap B)\)或\(P(A,B)\)表示联合概率，即\(A\)和\(B\)同时发生的概率。
• \(P(A|B)\)表示条件概率，即\(B\)发生时\(A\)发生的概率。
• \(P(A;\boldsymbol\theta)\)表示密度函数以\(\boldsymbol\theta\)为参数时\(A\)发生的概率。

琴生不等式：\(f(E(X))\leq E(f(x))\)

EM算法用于处理数据的缺失值。对于随机变量\(Z\)和参数\(\boldsymbol\theta\)都未知的概率分布模型\(P(X\cap Z;\boldsymbol\theta)\ ,\quad X=\{x_1,x_2,\cdots,x_i,\cdots,x_n\}\ ,\ i=1,2,\cdots n\)，定义概率分布函数\(Q_i(k)\ ,\quad Q_i(k)\geq0\ ,\ \sum_{k\in Z}Q_i(k)=1\)，有对数似然函数\(l\)：

\[l(\boldsymbol{\theta})=\sum_{i=1}^m\log P(x_i;\boldsymbol{\theta})=\sum_{i=1}^m\log \Big(\sum_{k\in Z}P(x_i\cap z_i=k;\boldsymbol{\theta})\Big) \]

根据琴生不等式，有：

\[l(\boldsymbol{\theta})=\sum_{i=1}^m\log \Big(\sum_{k\in Z}\frac{Q_i(k)P(x_i\cap z_i=k;\boldsymbol{\theta})}{Q_i(k)}\Big)\geq\sum_{i=1}^m\sum_{k\in Z}Q_i(k)\log \Big(\frac{P(x_i\cap z_i=k;\boldsymbol{\theta})}{Q_i(k)}\Big) \]

试图求\(\max_\boldsymbol{\theta}l(\boldsymbol{\theta})\)，欲使等号成立，则\(Q_i(k)=P(z_i=k|x_i;\boldsymbol{\theta})\)。

步骤：

1. 令\(Q_i(k)=P(z_i=k|x_i;\boldsymbol{\theta})=\frac{P(x_i|z_i=k)P(z_i=k)}{\sum_{l\in K}{P(x_i|z_i=l)P(z_i=l)}}\)；
2. \(\theta_k^{new}=\arg\max_{\boldsymbol{\theta}}\sum_{i=1}^m\sum_{k\in Z}Q_i(k)\log \Big(\frac{P(x_i\cap z_i=k;\boldsymbol{\theta})}{Q_i(k)}\Big)\)；

迭代更新\(\boldsymbol{\theta}\)直至收敛。

转载声明