监督学习常见算法
GDA(高斯判别分析)
多个样本联合概率等于每个的乘积:
\[P(\boldsymbol{Y}|\boldsymbol{X}) = \prod_{i=1}^{m} P(y_i| x_i) \]
高斯判别分析试图求出\(\hat y={\arg\max}_y{P(\boldsymbol x|y)P(y)}\ ,\quad y\in\{0,1\}\)。
多元高斯分布:
有\(n\)维随机向量\(\boldsymbol{x}=\begin{bmatrix}x_1&x_2&\cdots&x_n\end{bmatrix}^T\),存在\(\boldsymbol{\mu}=\begin{bmatrix}\mu_1&\mu_2&\cdots&\mu_n\end{bmatrix}^T\)、\(\boldsymbol{\Sigma}=\begin{bmatrix}\text{Cov}(x_1,x_1)&\text{Cov}(x_1,x_2)&\cdots&\text{Cov}(x_1,x_n)\\\text{Cov}(x_2,x_1)&\text{Cov}(x_2,x_2)&\cdots&\text{Cov}(x_2,x_n)\\\vdots&\vdots&\ddots&\vdots\\\text{Cov}(x_n,x_1)&\text{Cov}(x_n,x_2)&\cdots&\text{Cov}(x_n,x_n)\\\end{bmatrix}\)、\(\boldsymbol{\Lambda}=\boldsymbol{\Sigma}^{-1}\)。
若\(\boldsymbol{x}\)的联合概率密度为:\[f(\boldsymbol x)=(2\pi)^{-\frac{n}{2}}{\mid\boldsymbol{\Sigma}\mid}^{-\frac{1}{2}}e^{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T\boldsymbol{\Lambda}(\boldsymbol{x}-\boldsymbol{\mu})} \]则\(\boldsymbol{x}\)服从\(n\)元高斯分布。其中\(\mid\boldsymbol{\Sigma}\mid\)为\(\boldsymbol{\Sigma}\)的行列式。
当\(\boldsymbol{x}\)各个分量都相互独立时\(\boldsymbol{\Sigma}\)为对角矩阵。
对于能分成两类的样本\(X=\{\boldsymbol x_1,\boldsymbol x_2,\cdots,\boldsymbol x_m\}\ ,\quad \boldsymbol{x}_j=\begin{bmatrix}x_{j,1}&x_{j,2}&\cdots&x_{j,n}\end{bmatrix}^T\ ,\ j=1,2,\cdots,m\),其类别\(\boldsymbol{Y}\thicksim B(\phi)\ ,\quad\phi=\frac{\sum_{j=1}^mI\{y_j=1\}}{m}\ ,\ \boldsymbol{Y}=\begin{bmatrix}y_1&y_2&\cdots&y_m\end{bmatrix}^T\),对于每类样本有:
指数型分布族:分布律或概率密度满足\(P(y;\boldsymbol{\eta})=b(y)e^{\boldsymbol{\eta}^TT(y)-a(n)}\),其中\(\boldsymbol{\eta}\)为自然参数,通常充分统计量\(T(y)=y\),固定参数\(a\)、\(b\)、\(T\)上公式可以定义一种概率分布。
\(\begin{cases} x\mid y=1\thicksim ExpFamily(\mu_1)\\ x\mid y=0\thicksim ExpFamily(\mu_0)\end{cases}\)\(\Rightarrow\)\(P(y=1\mid x)\text{是logistic函数}\)。
NBM(朴素贝叶斯)
贝叶斯公式:
\[P(B_i\mid A)=\frac{P(B_i)P(A\mid B_i)}{\sum_{j=1}^n P(B_j)P(A\mid B_j)} \]
有\(m\)个样本,每个样本有\(n\)个属性:\(\boldsymbol{x}=\begin{bmatrix}x_{1,1}&x_{1,2}&\cdots&x_{1,n}\\x_{2,1}&x_{2,2}&\cdots&x_{2,n}\\\vdots&\vdots&\ddots&\vdots\\x_{m,1}&x_{m,2}&\cdots&x_{m,n}\end{bmatrix}\);
样本的类别:\(\boldsymbol{y}=\begin{bmatrix}y_{1}\\y_{2}\\\vdots\\y_{m}\end{bmatrix},y_j\in\mathcal{y}\),其中\(\mathcal{y}=\{c_1,c_2,\cdots,c,\cdots,c_p\}\)含\(p\)个类别;
对于一个样本\(x\),选择能使后验概率\(P(c\mid x)\)最大的\(c\)作为\(x\)的类别\(\hat{y}\)。朴素贝叶斯的训练过程就是基于训练集\(\boldsymbol{x}\)来估计后验概率\(P(c\mid \boldsymbol{x}_j)\),设\(\forall j=1,2,\cdots m\),\(x_{j}\)的每个属性都是相互独立的,则有\(P(c\mid \boldsymbol{x}_j)=\frac{P(c)P(\boldsymbol{x}_j\mid c)}{P(\boldsymbol{x}_j)}=\frac{P(c)}{P(\boldsymbol{x}_j)}\prod_{i=1}^nP(x_{j,i}\mid c)\)。
$$\hat{y}_j={\arg\max}_{c\in\mathcal{y}}{f_j(c)},$$ $$f_j(c)={P(c)\prod_{i=1}^{n}{P(x_{j,i}\mid c)}}$$ $f_j(c)$解释为 $\boldsymbol{x}_j$的类别为$c$的概率 与 在$\boldsymbol{x}_j$的类别为$c$条件下$x_{j,i}$取当前值的概率 之积 之积,就是用于比较的后验概率了。分母$P(\boldsymbol{x}_j)$通常是定值故忽略。求函数能使\(f(x)\)取得最大值的所有\(x\)值:
\[{\arg\max}_{x\in S \subseteq x}{f(x)}=\{x\mid x \in S \cap \forall t\in S:f(t)<f(x)\} \]
朴素贝叶斯中样本属性等都是随机变量,其分布函数(律)中参数即训练参数,利用极大似然估计去确定这些参数。
极大似然估计
假定样本满足某一分布,试图求这个分布的分布函数(律)中参数。
\(\mathcal{x}_c\)为由\(\boldsymbol{x}\)中类别为\(c\)的样本组成的集合,则:
通常为了便于后续计算取对数,然后的对数似然函数:
NN(人工神经网络)
将生物神经元抽象为一种数学模型。每一个神经元都有敏感程度不同的突触用来接收信号,无论这些输入信号多么强或多么弱,神经元的输出总在一个狭窄的区间里,这是加权求和再进行某种非线性变换的结果。NN有很多参数,并且NN在数据较多时效果较好。
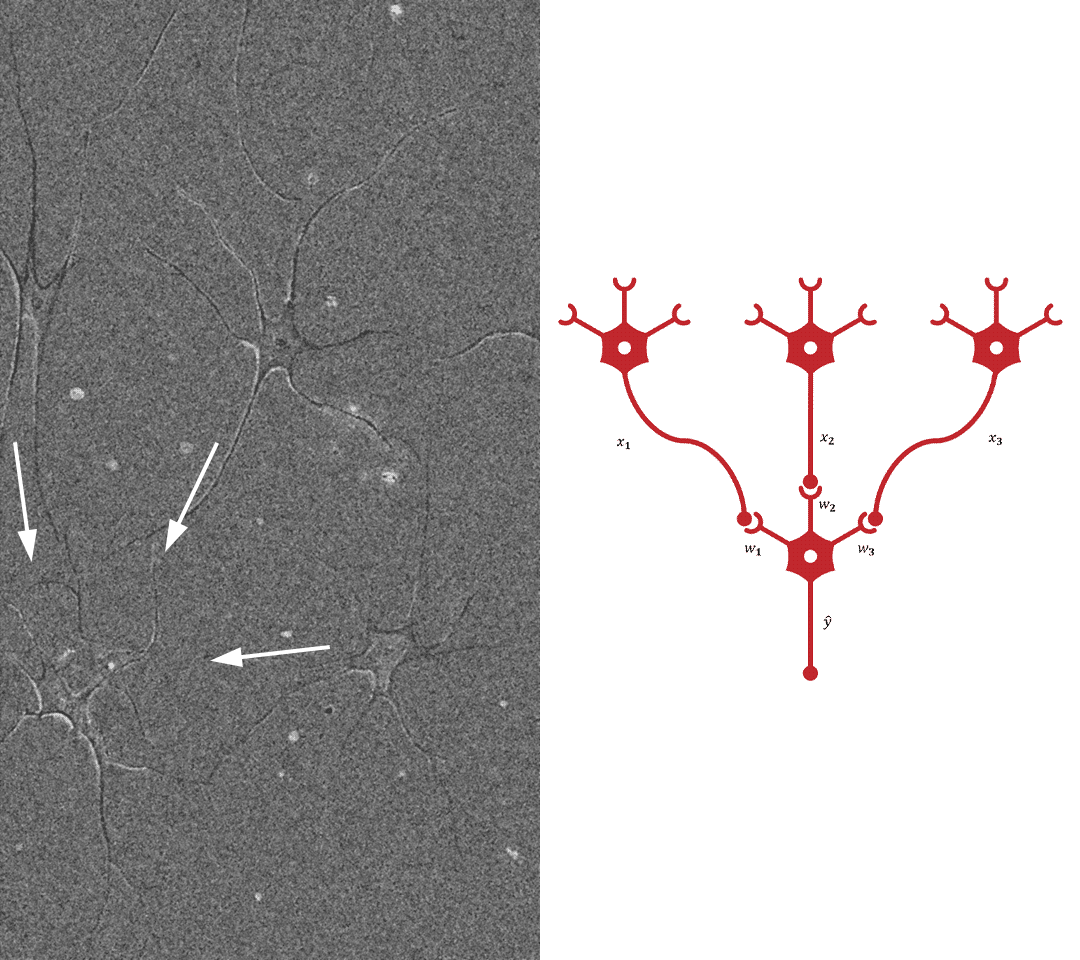
NN原理简单,如下图所示:

上图还包括了BP算法(误差逆传播算法),它为NN更新每个神经元的权值。
对样本\(\boldsymbol{X}=\begin{bmatrix}x_0&x_1&x_2&\cdots&x_{I_0}\end{bmatrix}^T\),NN使\(\boldsymbol{X}\)作为无前驱神经元的神经元的输出(注意不是输入),并试图获得无后继神经元的一个或几个神经元的输出作为神经网络的输出。这些无前驱的神经元构成输入层,无后继的神经元构成输出层,其余按照其连接次序构成隐层(可以有许多层),隐层和输出层神经元会参与误差逆传播的过程而输入层不会,输入层也没有阈值\(x_0\)。所谓阈值就是一个固定的值加在输入的一个特定位置中一起交给神经元计算,对应于阈值的权值也会在逆传播中更新,但是“阈值的误差”传递到哪里去了呢?消失了,因为阈值类似输入层神经元,是不参与逆传播的。NN的学习过程为计算每一个神经元的权重\(\boldsymbol{W}\)(其实就是分割数据点的超平面表达式的参数)。
权重\(\boldsymbol{W}\)是三维的但不是“三维矩阵”,因为每层的尺寸未必相同。左上角标\(l\)代表层序号,\(l=0\)代表输入层。\(L\)为总层数,也叫深度,包含许多隐层的复杂神经网络形成深度学习。\(J_l\)为第\(l\)层神经元个数,也叫宽度。\(I_l\)为第\(l\)层的输入值的属性数,它可以是样本\(\boldsymbol{X}\)的属性数也可以是\(J_{l-1}+1\),即\(I_l=J_{j-1}\)。上图的\(I\)和\(J\)都没写角标,但注意不同层的\(I\)或\(J\)往往不相同。
Python3简单实现:点我看代码
SVM(支持向量机)
SVM有严格的数学理论支持,不依靠统计方法;利用核函数可以处理非线性分类任务;最终决策函数只由少数样本所确定(不代表SVM会丢弃样本,SVM复杂度是和样本数有关的),所以SVM避免了维数灾难并对缺失值敏感。SVM算法时间和空间复杂度都较大,适用于少量样本分类任务。\(\boldsymbol{x}=\begin{bmatrix}x_{1,1}&x_{1,2}&\cdots&x_{1,n}\\x_{2,1}&x_{2,2}&\cdots&x_{2,n}\\\vdots&\vdots&\ddots&\vdots\\x_{m,1}&x_{m,2}&\cdots&x_{m,n}\end{bmatrix}^T\)为\(m\)条样本(没错需要转置,这里训练集的每条样本的属性都是竖着的一列),它的类别为\(\boldsymbol{y}=\begin{bmatrix}y_{1}&y_{2}&\cdots&y_{m}\end{bmatrix}^T\)。对于新样本\(\boldsymbol{x}^+\),SVM试图求解:
SVM通过改变参数\(\boldsymbol{\alpha}\)来使\(f\)正确分类:
其中\(W\)是一个函数:
然后这个\(\hat{\boldsymbol{\alpha}}\)就用来预测新的数据了(之前参数用的都是\(\hat{\boldsymbol{\theta}}\))。\(\boldsymbol{\alpha}\)初值为\(\boldsymbol{0}\)。\(C\)为常数,描述SVM对个别数据分类出错的容忍程度。函数\(g\)可以认为是sigmoid函数。\(W\)里面还有个\(\kappa\),\(\kappa\)是核函数,也是一个函数。
常见核函数:
| 核函数 | \(\kappa(\boldsymbol{x}_j,\boldsymbol{x}_k)\) | 参数说明 |
|---|---|---|
| 线性核 | \(\boldsymbol{x}_j^T\boldsymbol{x}_k\) | |
| 多项式核 | \((\boldsymbol{x}_j^T\boldsymbol{x}_k)^d\ ,\quad d\geq 1\) | \(d\)为多项式次数 |
| 高斯核 | \(e^{\frac{{\Vert\boldsymbol{x}_j-\boldsymbol{x}_k\Vert}^2}{-2\sigma^2}\ ,\quad \sigma>0}\) | \(\sigma\)为width |
| 拉普拉斯核 | \(e^{\frac{{\Vert\boldsymbol{x}_j-\boldsymbol{x}_k\Vert}}{-\sigma}\ ,\quad \sigma>0}\) | |
| sigmoid核 | \(\tanh(\beta\boldsymbol{x}_j^T\boldsymbol{x}_k+\theta)\ ,\quad\beta>0,\theta<0\) |
取\(\boldsymbol{\alpha}\)中的值\(\alpha_j\)、\(\alpha_k\),注意一次取两个值,则有:
以上的似乎使得“支持向量机”这个名字变得无法理解。那么请看以下:
\(\boldsymbol{x}=\begin{bmatrix}x_1&x_2&\cdots&x_n\end{bmatrix}\)则L2范数\(\|\boldsymbol{x}\|=\sqrt{\sum_{i=1}^n{{\mid x_i\mid}^2}}\)
在样本空间中类别为\(y\in\{-1,+1\}\)的任意一个点\(\boldsymbol{x}_j=\begin{bmatrix}x_{j,1}&x_{j,2}&\cdots&x_{j,n}\end{bmatrix}^T\)到超平面\(\boldsymbol{w}^T\boldsymbol{x}+b=0\)的距离为函数间隔\(\hat{\gamma}=y(\boldsymbol{w}^T\boldsymbol{x}+b)\)。但是函数间隔会受到参数影响,超平面不变情况下参数同乘一个数的话函数间隔会变,所以采用几何间隔\(\gamma_j=y_j\big((\frac{\boldsymbol{w}}{\|\boldsymbol{w}\|})^T\boldsymbol{x}_j+\frac{b}{\|\boldsymbol{w}\|}\big)=\frac{\hat{\gamma}_j}{\|\boldsymbol{w}\|}\)描述样本点\(\boldsymbol{x}_j\)到超平面的距离。\(\boldsymbol{w}=\begin{bmatrix}w_1&w_2&\cdots&w_n\end{bmatrix}\)为法向量。
\(\boldsymbol{x}_j\)可能是线性不可分的,则需要\(\varphi(\boldsymbol{x})\)函数将自变量映射至更高维度的特征空间,因为如果原始空间是有限维则必然存在一个高维特征空间使样本可分。SVM并不是采用多么复杂的界线去分隔数据,而是为数据添加一些“计算属性”从而将数据映射到高维空间中再线性分割。
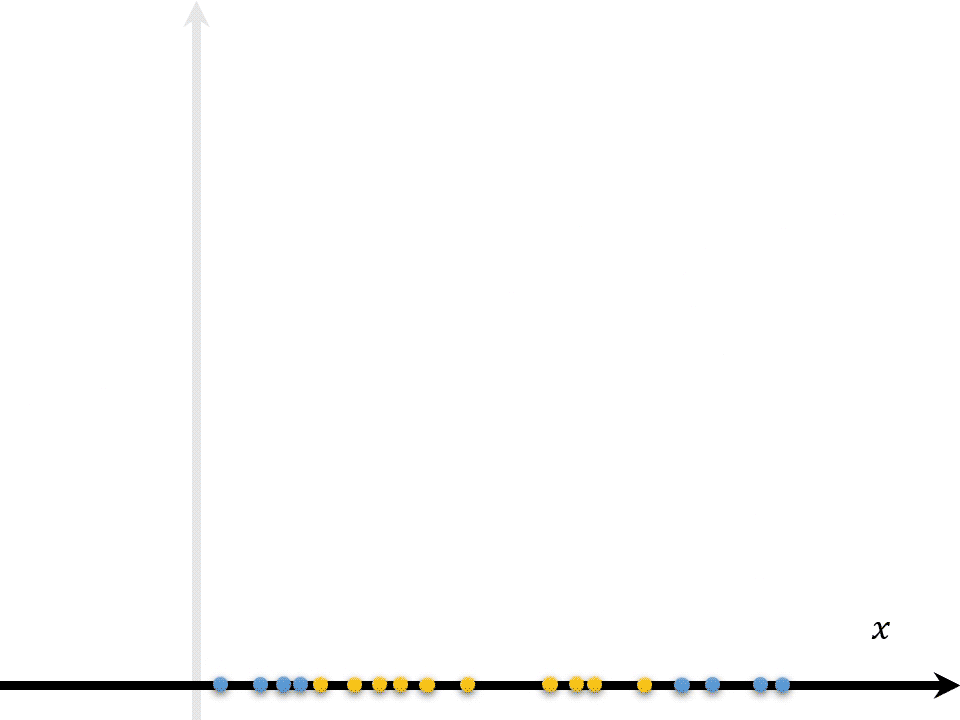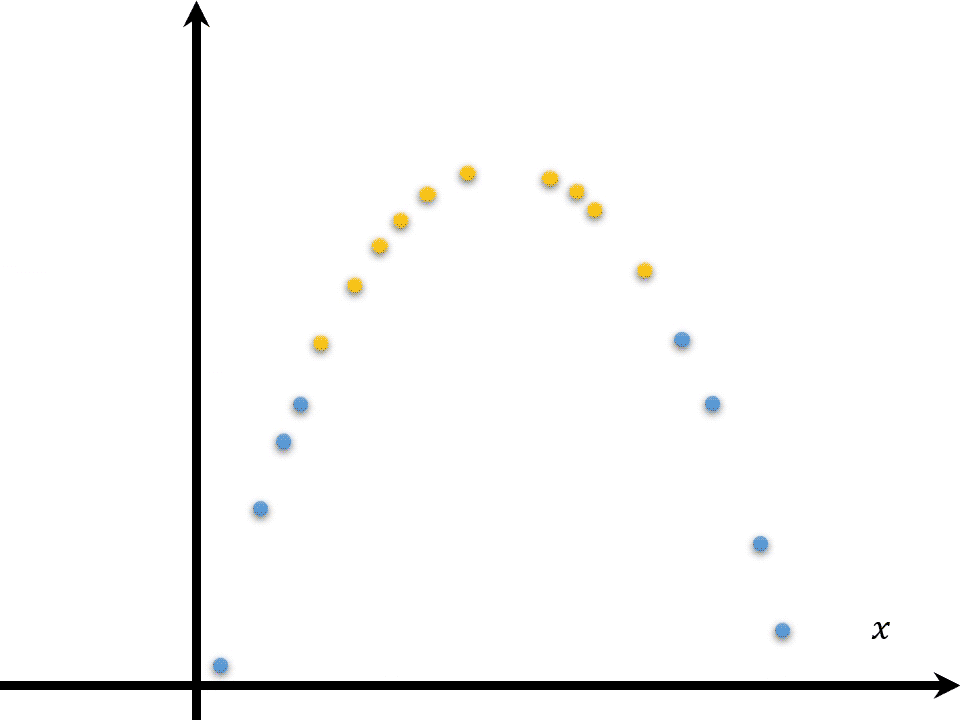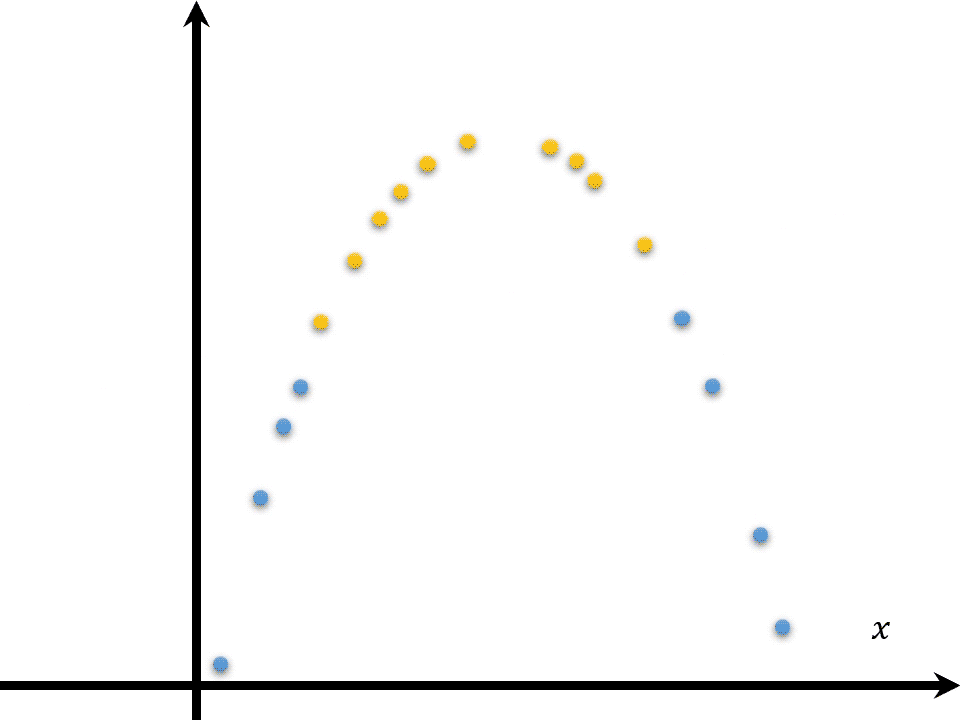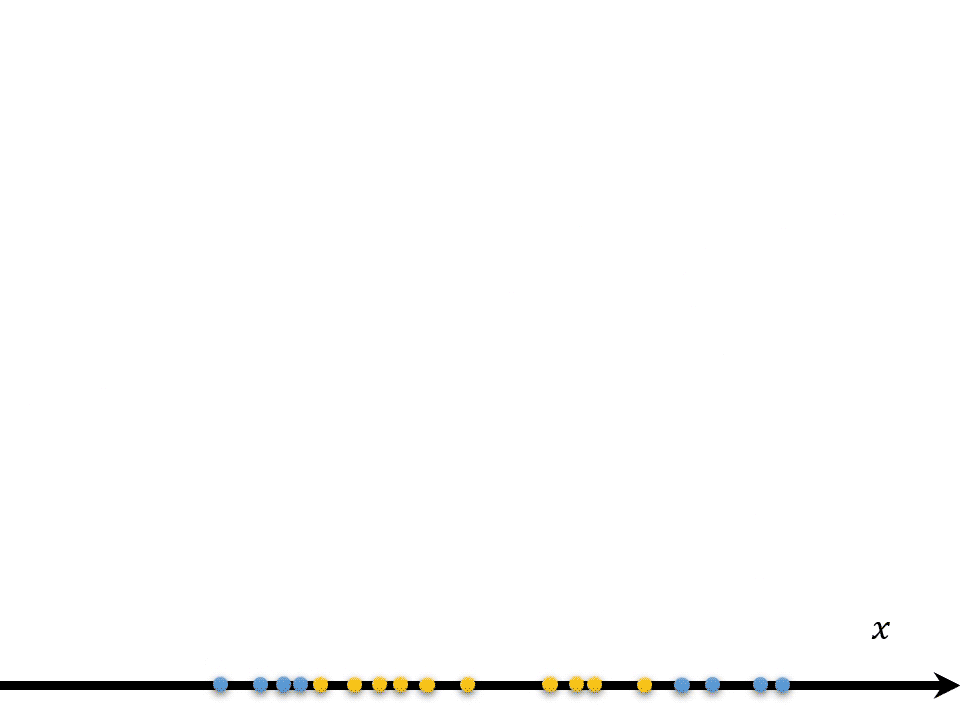
其中\(\kappa(\boldsymbol{x}_j,\boldsymbol{x}_k)\)为核函数。这样就不用去计算函数\(\varphi\)了,\(\varphi(\boldsymbol x_j)^T\varphi(\boldsymbol x_k)\)具体形态参见上文核函数表。
任何一个求极大值的线性规划问题都有一个求极小值的对偶问题与之对应,反之亦然。对偶问题可能比原问题更易求解。SVM试图找到\(\boldsymbol{w}\)、\(b\)使\(\gamma\)最大,将不同类别的样本分开,并且这个超平面尽可能远离样本。所以优化目标为:
令\(\hat{\gamma}=1\)则等价于(便于计算):
其拉格朗日函数:
其对偶问题:
当超平面将样本不同类别样本分开时,能使上面的\(\hat\gamma=1\)成立的\(\boldsymbol{x}\)即为支持向量。两个不同类别的支持向量到超平面的距离之和为\(\gamma=\frac{2}{\|\boldsymbol{w}\|}\)。
同时易得\(w_i=\sum_{j=0}^m{\alpha_j y_j x_{j,i}}\),\(\boldsymbol{w}=\sum_{j=0}^m{\alpha_j y_j \boldsymbol{x}_j}\)。
拉格朗日乘数法:
在一组条件\(\phi(\boldsymbol{x})=\begin{bmatrix}\phi_1(\boldsymbol{x})\\\phi_2(\boldsymbol{x})\\\vdots\\\phi_n(\boldsymbol{x})\end{bmatrix}=\boldsymbol{0}\ ,\quad i=1,2,\cdots,n\)下求函数\(f(\boldsymbol{x})\)极值点(如有),即:\[\min_w f(\boldsymbol{x})\quad \text{s.t.}\ \phi(\boldsymbol{x})=\boldsymbol{0} \]有拉格朗日函数:
\[L(\boldsymbol{x},\boldsymbol\alpha)=f(\boldsymbol{x})+\sum_{i=1}^n{\alpha_i \phi_i(\boldsymbol{x})} \]其中\(\boldsymbol\alpha\)为拉格朗日乘数。
令\(\frac{\partial{L}}{\partial{\boldsymbol{x}}}=0\)、\(\frac{\partial L}{\partial \boldsymbol\alpha}=0\)得:
\(P(\boldsymbol{x}^*)\)是驻点\(\Leftarrow \exists \boldsymbol{\alpha}^*\quad\text{s.t.}\ \frac{\partial{L(\boldsymbol{x}^*,\boldsymbol{\alpha}^*)}}{\partial\boldsymbol{x}}=0,\frac{\partial{L(\boldsymbol{x}^*,\boldsymbol{\alpha}^*)}}{\partial\boldsymbol{\alpha}}=0\)。
选择能让样本线性可分的核函数实际上是一件非常困难的事情,两类样本的边界可能十分模糊,当SVM将样本完全分开时基本上已经过拟合了。这时要采用软间隔,允许少量样本没有被正确分类。所以优化目标为:
其对偶问题:
其中\(\xi\)为松弛变量,\(C\)为常量,\(C>\alpha_j>0\Rightarrow y_j(\boldsymbol{w}^T\boldsymbol{x}_j+b)=1\)。就得到上文中的函数\(W\)。
转载声明
 机器学习监督学习常见算法。混合高斯模型GDA、朴素贝叶斯NBM、神经网络NN、支持向量机SVM各种公式。斯坦福公开课。
机器学习监督学习常见算法。混合高斯模型GDA、朴素贝叶斯NBM、神经网络NN、支持向量机SVM各种公式。斯坦福公开课。

