逻辑回归与神经元模型

转载源

空间平面的方程

这是一个似曾相识的方程👇

\[b+\sum_{n=1}^Nx_n\theta_n\bm{i}_n=0 \]

没错，它描述了空间中的一个平面。其关于每一个坐标轴都有斜率\(\theta_i\)，而\(\bm{i}_n为这个轴方向的单位向量\)。在\(N<=3\)时我们能将这个平面很直观地表达出来，但是当\(N\)更高的时候我们难以想象这个平面的样子，显然，没有人见过比三维更高维度的空间。不过无论如何，它总是将空间分成两个部分。想象这个平面就是地平面，它恰好将一片混沌划分为天与地……

很久很久以前盘古在黑暗中大斧一挥扰动了均质，阳清为天，阴浊为地，两类物质按照他们自身的性质分成了两部分。几千年以后，斯坦福有一个分不清楚天和地的无人机头冲下倒立悬空。

逻辑回归

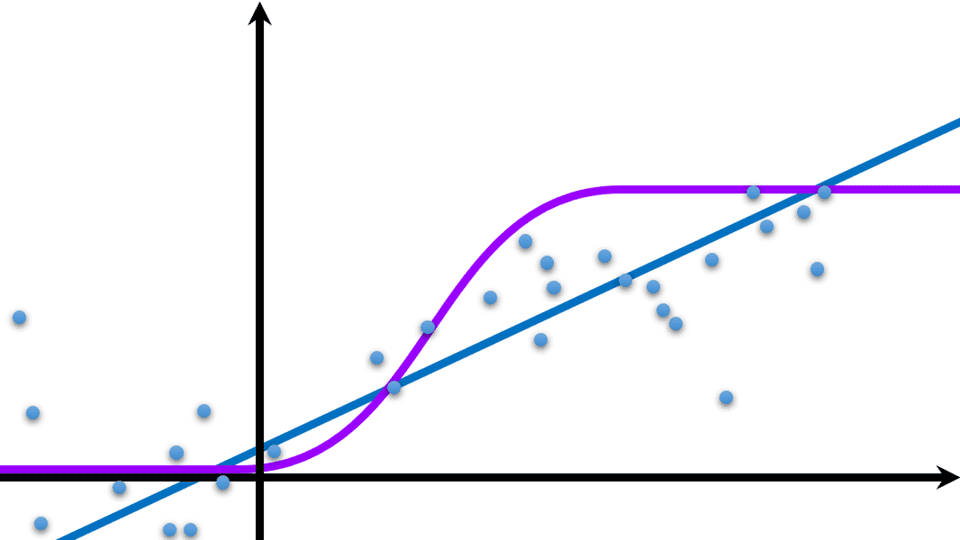
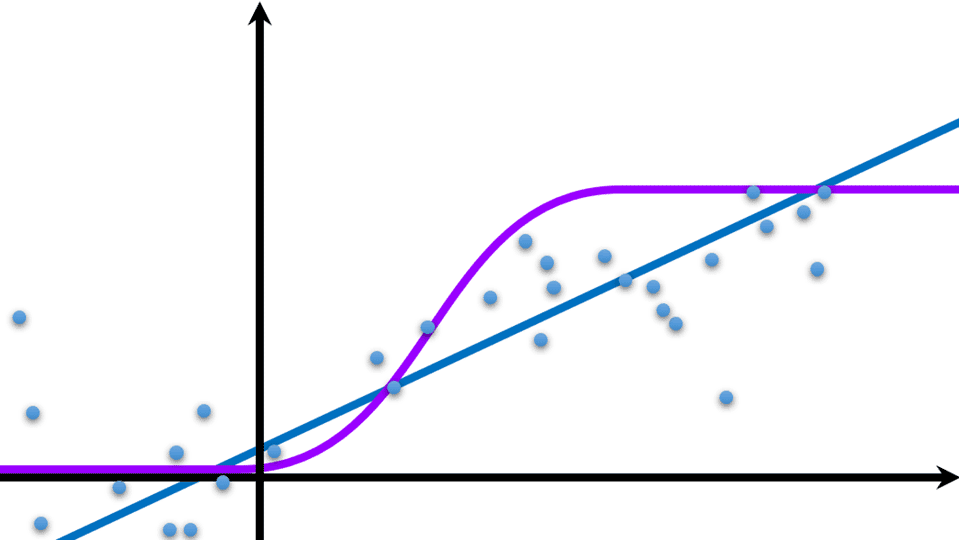
相比于线性回归（下图中蓝线所示为线性回归结果），逻辑回归（下图紫线）的名字具有少许迷惑性。有了逻辑回归，可以将线性回归的输出限制在\((0,1)\)内。逻辑回归之“逻辑”并不强调逻辑回归的逻辑特性，而是描述其输出在\((0,1)\)内从而实现了能对输入类型做出逻辑判断的特点。可以理解为逻辑回归之“逻辑”表示逻辑值0和1即True和False，而非我们常说的逻辑。逻辑回归之“回归”也非线性回归之“回归”，线性回归解决回归问题而逻辑回归解决分类问题，下图中的数据点并没有均匀分布在逻辑回归结果曲线两侧。其分布函数是sigmoid函数（即S型生长曲线）。

分布名称	分布函数\(P(\xi\leq x)\)	概率密度
Logistic分布	\(sigmoid(x)=\frac{1}{1+e^{-x}}\)	\(sigmoid^\prime(x)=sigmoid(x)(1-sigmoid(x))\)

神经元模型

我们需要划出一个地平面，将混沌的清浊阴阳划分开来，虽然天地早在千年之前已经分开，但是面前一堆未分类的数据就好似一片混沌。或者更准确地说，地平面就在那里，我们训练模型只是将它找出来，找到一条完美的，或者说是恰到好处的地平面。我们先假定地是平的或者将地面近似为一个平面，然后判断任意一点是否在地面上方，之后我们再去看一看这个点是不是真的在地面上方，然后在根据观测结果和判断结果来调整平面的位置，直到这个平面与地面重合为止，即收敛。

根据观测结果和判断结果之间的差异使用误差函数来计算，这种差异可以叫做误差。损失函数与误差函数作用相同，概念有微小差异，不同损失函数对误差有其独有的量化方式。比如交叉熵损失函数：

\[J(\boldsymbol{\theta})=-\frac{1}{m} \sum_{j=1}^m \Big( y_j \log{ \hat{y}_j + (1-y_j) } \log{ (1- \hat{y}_j )} \Big)=-\frac{1}{m} \sum_{j=1}^m \Big( y_j \log{\big( h_{\boldsymbol{\theta}_j}(\boldsymbol{x})\big)} + (1-y_j) \log{ \big(1- h_{\boldsymbol{\theta}_j}(\boldsymbol{x}) \big)} \Big) \]

至于如何来调整平面位置，也就是调整斜率向量\(\bm{\theta}=\theta_n\bm{i}_n\)，有EM算法、梯度下降法等等很多的都可以做到。

我们在上述过程中已经隐式地加入了一个激活函数那就是：

\[\text{点是否在地面上方}=\bold{1}(\text{点的纵坐标}>0) \]

实际上我们通常用sigmoid或者类似非线性函数来充当激活函数，但是如果不用激活函数，就只是将点的坐标与一向量相乘，其结果能够反映这一点的坐标而没法反映这一点是飞在天上还是埋藏在地底下。

神经元模型是模拟生物神经元工作的数学函数，其对一组输入分别加权并且相加并通过激活函数产生输出，平面的截距则作为一个内部状态被神经元携带。关于我们之前的假设：地面是平的，如果想表示曲面，不妨用很多平面来近似，这时众多神经元以一定的方式彼此连接已经构成神经网络。