[ZJOI2020]字符串
题目链接
以下字符串采用Python记法。
题意
定义平方串形如 $PP$, 给定母串 $S$, 要求回答 $q$ 组询问,每组询问形如 $S[l:r]$ 有多少个本质不同平方子串。
数据范围:$|S|, q \le 2\times10^5$.
题解
这里run的记法是 $(i, j, p)$ 表示 $S[i:j]$ 的最小周期为 $p$, 且该性质不可向左右扩展。
任意一个平方子串 $S[i:j]$ 必然含于恰好一个run $(i_r, j_r, p)$ 使得 $2p \mid j-i, i_r \le i<j \le j_r$.
先求出所有run. 一个run $(i, j, p)$ 的平方子串形如 $S[u:u+2kp]$, 其中 $k \in \mathbb N^*$, $i \le u<u+2kp \le j$.
考虑其上一次出现为 $S[v:v+2kp]$, 那么对于 $r \ge u+2kp$ 且 $v<l \le u$ 的询问 $(l, r)$ 其贡献 $1$ 的答案。把它拆成前缀相减的形式,即对 $r \ge u+2kp, l \le u$ 的询问 $(l, r)$ 贡献 $1$ 的答案,并对 $r \ge u+2kp, l \le u$ 的询问 $(l, r)$ 贡献 $-1$ 的答案。
考虑把这个过程画到坐标上。那么也就是,一组如此的 $(i, j, p, u, k)$ 将在 $(u, u+2kp)$ 上放置权值 $+1$, 在 $(v, u+2kp)$ 上放置权值 $-1$, 每次询问 $(l, r)$ 即询问 $\begin{cases}x \ge l\\y \le r\end{cases}$ 区域内的所有点权值和。
我们注意到,对于 $u \ge i+p$, 均有 $v=u-p$, 否则 $v<i$. 我们首先特殊处理这些 $i \le u<i+p$ 的串带来的 $-1$ 权值。每个如此的 $(i, j, p, k, u)$ 都与本原平方串 $S[u+2(k-1)p:u+2kp]$ 对应,不同的该五元组对应的本原平方串不同,所以总数为 $O(n\log n)$ 级别。$v$ 可以用哈希表查询。把询问按照 $r$ 离线,分块维护,所以这部分时间复杂度 $O(n\log n+q \sqrt n)$, 空间复杂度 $O(n\log n)$.
我们接下来还需要考虑点 $(u, u+2kp)$ 及点 $(u-p, u+2kp)$.
注意到枚举 $(i, j, p, k)$ 为 $O(n)$ 级别。对于一个Run和枚举的 $k$, 我们发现两类权值的贡献上,放置的点都形如 $(x, x+b)$ ($L \le x \le R$) 的形式。问题转化为:有一些斜线 $(L, R, b, v)$ 表示对于所有 $x \in [l, r], y=x+b$ 的 $(x, y)$ 都放置 $v$ 的权值,求 $\begin{cases}x \ge l\\y \le r\end{cases}$ 这块区域的权值和。
下图是查询 $ababababa$ 中 $[1:8]$ 区间的情况。黑斜线表示 $+1$, 红斜线表示 $-1$. (画图工具:GeoGebra)
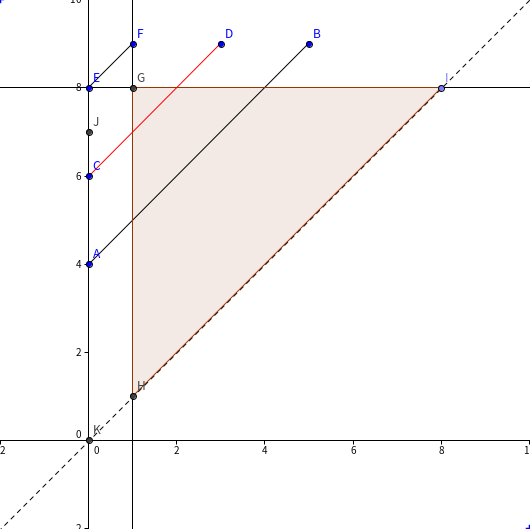
把它拆成两个区域 $\begin{cases}b \le r-l\\y \le r\end{cases}$ 和 $\begin{cases}b \le r-l\\x<l\end{cases}$ 内权值和的差,按照 $r-l$ 离线,对 $x, y$ 各自区间修改、区间查询,仍然分块,时间复杂度 $O((n+q)\sqrt n)$.
下图直观地展示了如此拆分的意义。
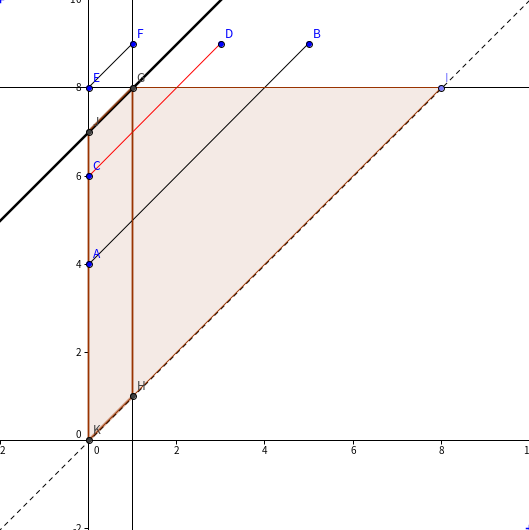
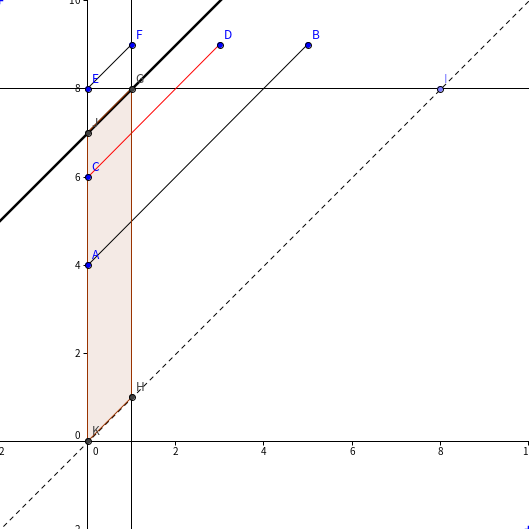
综上所述,本题在 $O((n+q)\sqrt n)$ 时间、$O(n\log n+q)$ 空间内得到解决。如果把分块全部换成线段树,时间复杂度是 $O(n\log^2 n+q \log n)$.



