深入浅出无人机姿态，欧拉角，四元数，指数表示及数据转换与程序实现

熟悉无人机的朋友一定常常听到姿态，这两个字，无人机工程师一定觉得这实在太熟悉了，方位余弦，四元数，可能有些朋友也用过指数表示方法。Ok，这些内容确实不难，本文也会直接给到大家相关公式，可以拿来在程序中直接使用。但MR.城堡不知道各位有没有过滤过这些问题：无人机为什么需要姿态描述？旋转为什么有三个呢？为什么耦合不直接用自由度表示出来呢？为什么要12个状态（说15个状态的朋友，线性加速度也放了进去，后文将告诉你这是不必要的），未来有没有可能需要更多状态？这些姿态表示方法有什么区别？有没有其它姿态表示方法呢？什么叫做万向节锁死呢？为什么锁死就控制不了？等等

这些问题有些工程师可以凭直觉得到答案，有些比如未来是否需要更多状态？为什么选择某一种姿态描述方式？万向节锁死的本质解释，以及不能控制的原因？等等，可能就会比较吃力，然而这些却很重要，当我们把这些理论与无人机系统实物联系起来时，不但可以用更低的成本，做出更好的产品，更能丰富我们对无人机的理解，形成对技术和趋势的预判。

通过前面的专栏文章：城堡里学无人机：无人机导航之玩转坐标系，城堡里学无人机：如何处理GPS数据获取无人机状态信息？，我们知道无人机如何获取位置和速度状态，并转换到NED坐标平面内。但这并不足以让我们全面了解无人机的运动情况，换句话说，相同的位置中，无人机可能有不同的运动姿态。举例来说，一架多旋翼无人机在不同时间经过位置

时，前一次为水平飞行，后一次为垂直飞行。虽然位置坐标相同，但运动方式却如此不同。这时我们需要一些额外的信息才能够精确描述无人机的飞行状态，这也就是本文所涉及的内容：无人机姿态。

上面是用一个简单的例子说明一下，但不具有普遍性，下面从理论上浅析一下为什么外环信息出来了还要内环姿态。

多旋翼无人机的姿态可以通过机体坐标系和NED坐标系之间的关系来进行定义。在多旋翼机型介绍中，大家已经了解了多旋翼无人机的姿态控制方式。很容易看出多旋翼无人机具备六个自由度（Degree of Freedom, DOF），沿机体坐标系三轴的线性运动以及绕机体坐标系三轴进行的旋转运动。

然而很容易看出来的内容，想搞清楚why却往往并不容易。

关于自由度，在结构力学或者分析力学中，它的定义是：确定一个质点的位置所需要的独立坐标的个数。物理有的时候比较抽象，大家可以直接通过线性代数里的线性空间来理解，线性空间中我们说到一个子空间，它的维度（Dim）就是张成（Span）这个空间的一组基（Bases）中相互独立向量的个数，我们可以在这里将dimension和DOF等同起来。因此，力学中的“独立坐标”，可以理解为“相互独立的基向量”。有兴趣的朋友可以结合流形，微分同胚来理解（当然，对于工程师而言，还是可以直接转换到矩阵变换的范畴内）

在无人机中有6个自由度，意味着我们需要六组基坐标来描述它的完整位置，这六组基就是无人机所在的空间中的三个坐标轴，以及围绕三个坐标轴的姿态角（请注意，这里不是说在中的一组基能有6个相互独立向量，因为研究对象已经不再是质点，而是刚体，刚体旋转位置描述也不能只用）。从位置到运动，就是导数了，这时6*2=12个状态。我们并不需要更多的向量来描述无人机位置，因此也不需要更多状态来描述无人机的运动，虽然有时候为了方便实现某些功能，或者扩展我们对于“运动”的理解，我们想要控制它的受力状态，我们会增加一些控制行为，比如针对加速度的控制，但这些变量不是描述无人机运动所必须的。

姿态的英文词汇有两个“attitude”或者“orientation”后者的意义更为明显，可以理解为“取向”“指向”，常用于卫星姿态描述中。

有多种方法对无人机旋转运动进行描述，最常见的是方向余弦和四元数及指数表现形式。但无论是哪一种，我们都可以理解为是按照某种表现方式提供一组基向量，来描述无人机旋转位置的三个自由度。但是它们却因为算法的不同，具有不同性质，这些性质将决定我们对它们的选择。

1)欧拉角

无人机围绕机体系三轴的运动可以分解为：绕轴的横滚运动，绕轴的俯仰运动以及绕轴的偏航运动。欧拉角直观地将无人机旋转姿态转化为机体坐标系和NED坐标系之间的夹角关系。

一说到角度，一定是同一个平面内线和线的关系或者相交平面之间的关系。在无人机坐标系中需要大家建立起六个面的抽象图形，机体坐标系下三个平面：

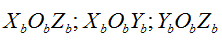
以及NED坐标系下三平面：

当我们确立了这六个平面之后，就可以描述无人机姿态了。我们定义横滚角,俯仰角,偏航角来分别描述无人机的横滚运动，俯仰运动，偏航运动。

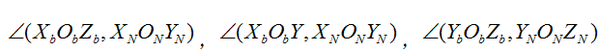
2)方向余弦

实现从NED坐标系到机体坐标系的数据变换有什么意义呢？无人机的旋转运动相对于无人机自身是没有任何意义的，因为它相对于自己永远是没有运动的，只有相对于地面（参考坐标系）才有意义。因此我们要用NED和机体坐标系间的关系来表述无人机旋转运动，无疑，矩阵就是描述旋转最好的工具了。

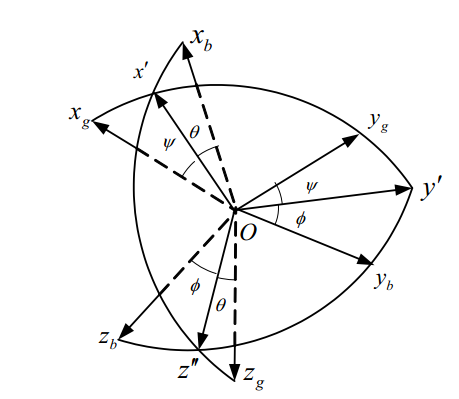
我们可以把无人机任意一次旋转按次序拆分为三个部分：绕轴的偏航运动、绕轴的俯仰运动、绕轴的横滚运动。每一次运动用一个旋转矩阵来描述就成为了下面的形式：

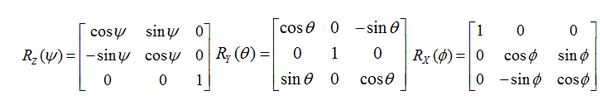
大家一定注意到这三个矩阵都是斜对称阵，喜欢矩阵的朋友可以自行思考一下，肯定可以挖掘出很多有趣的内容。容易得到从NED到机体坐标系的坐标变换矩阵（方向余弦矩阵）：

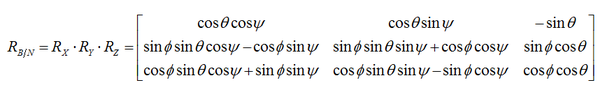
从机体坐标系到NED坐标系的方向余弦矩阵很容得到：

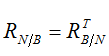
如此一来，我们就很容易实现两个坐标系下信息的相互转换。

3)不唯一与奇异性

在任何系统中，控制工程师首先关注的是系统方程解的唯一性和存在性。

欧拉角非常直观，但也存在两个问题：1.不唯一2.奇异性。这两者分别对应了解的唯一性和存在性。这两个问题从直观上比较难以描述，但从数学上借助方向余弦可以很清楚的解释。

不唯一性：举一个例子，令

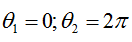
这时：

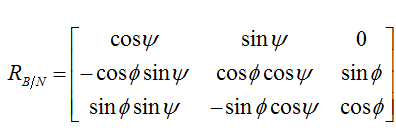
很容易看出，这种不唯一性是由三角函数的周期性引起的，不唯一性可能会出现系统运动不按照我们期望的方式进行。

奇异性（局部）：如果我们令：

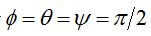
这会带来什么问题呢？在后面介绍无人机数学模型时，三个欧拉角与无人机本身的旋转角速度是通过一个矩阵进行关联的：

此时，零出现在分母上，这时控制器就没有办法处理被控对象的数学模型了，也就是我们所说的解不存在的情况，也将因此无法实现有效控制。这就是常说的“万向节锁死”。数学描述是不是非常直观明了呢？

上面的情况导致欧拉角的姿态描述方式在某些姿态情况下不可使用，这对于无人机控制而言是会带来一定风险的。因此我们需要在另外一种描述方法可以对无人机所有的姿态进行描述。

4)四元数

四元数是一种全局的姿态描述方法，换句话说，当使用四元数描述姿态的时候，纵使

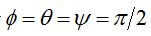
再次出现，描述方法依然有解。我们 直接验证一下就可以了，首先看一看如何从欧拉角获取四元数：

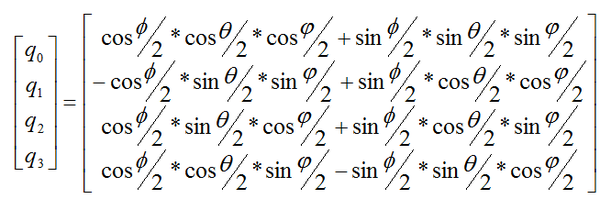
然后再对四元数进行归一化处理：

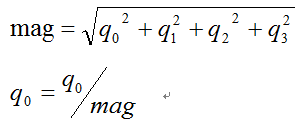
q1,q2,q3的归一化处理与q0相同。

请大家注意，此时，纵然出现90°的姿态角，由于没有出现分母为零的情况，因此依然有解。这只是很直观的验证，结合指数姿态表示方法：

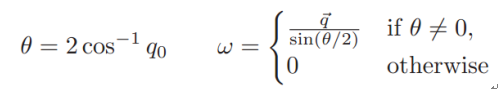而四元数的不唯一性可以通过下式看出：

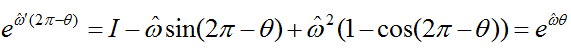因此，带入

时，R矩阵式一样的。

很容易获得从四元数到欧拉角的转换公式：

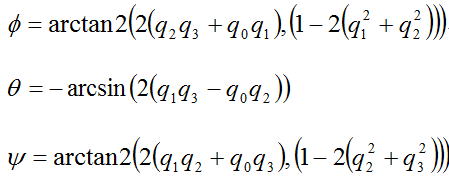
5)程序实现

从欧拉角到四元数的程序实现非常直接，并不需要想一般算法那样进行离散化，因为这里的转换公式并不对应时域函数，而是直接对应变量值，所以只要我们通过传感器获得可靠的姿态数据值后就可以直接带入公式求得对应姿态：

quat[0] =  chphi0 * chtheta0 * chpsi0 + shphi0 * shtheta0 * shpsi0;
quat[1] = -chphi0 * shtheta0 * shpsi0 + shphi0 * chtheta0 * chpsi0;
quat[2] =  chphi0 * shtheta0 * chpsi0 + shphi0 * chtheta0 * shpsi0;
quat[3] =  chphi0 * chtheta0 * shpsi0 - shphi0 * shtheta0 * chpsi0;

如是而已。

6）指数表现形式

指数表现形式在实际使用中比较少，但是对于理解另外两种旋转表现方式很有助益。它是既不是全局的，也具有奇异性。有兴趣的朋友可自行了解，推荐《A Mathematical Introduction to Robotic Manipulation》这本书。

相信大家通过本文应该可以直接获取无人机姿态数据的转换公式，并根据不同旋转运动描述方法的特点结合自己的需求进行数据转换（基坐标变换？不知这样的词汇合适么）。

有时我们面对的研究对象是可以碰触的物理实体，比如无人机，这当然会给我们带来很多好处，但过分陷入到对直观感受的依赖中，很有可能将自己引入主观的误区，就像一场狩猎游戏，好狐狸总是想方设法用猎人自己的思维来迷惑他。而数学却能简洁，工整，清晰的将我们研究对象的本质揭露出来，很多情况下这是我们凭自己的直观感受难以挖掘的，这也正如好的侦探，最后得出的结论也许很难在感情上接受它，却无法否认它是更加接近真相的推断。在无人机研究中畅快的运用数学就犹如身临一场狩猎或者探案冒险，抽丝剥茧，能得到一点点结论都会让自己心情久久畅快，有时会让自己惊讶的一天都沉迷其中，这种快乐也可以算作研究无人机的副产品吧：）。

转载自：无人机中的城堡