深度优先搜索

1.算法说明

　　[1]深度优先搜索主要基于栈来操作，即把初始节点沿着一条路径直到终点入栈，然后再返回访问分叉，沿着分叉直到终点入栈，以此反复，所以使用递归比较方便。

2.例子

例1： 有一长度为N(1 <= Ｎ <= 10)的地板，给定两种不同瓷砖：一种长度为1，另一种长度为2，数目不限。要将这个长度为N的地板铺满，一共有多少种不同的铺法？

　　代码：

#include "stdlib.h"   
#include "stdio.h"  

int g_size;
int g_result = 0;

//used表示已经铺上的大小
void dfs(int used)
{
    if (used > g_size)
        return;
    
    if (used == g_size){
        g_result++;
        return;
    }
    
    dfs(used + 1);
    dfs(used + 2);
     return ;
}

int main()
{
    printf("input size:");
    scanf("%d", &g_size);

    dfs(0);

    printf("result:%d\n", g_result);
    return 0;
}

 　　

例2：如图所示六角形中，填入1~12的数字，使得每条直线上的数字之和都相同。图中已经填好了3个数字，请计算星号位置所代表的数字是多少？

　　

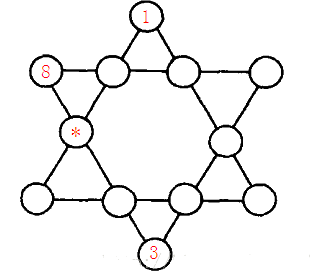
　　代码：

#include <stdio.h> 

int g_array[13] = {0};
int g_value[13] = {0};

// 参数x是当前要填充的位置
void dfs(int x)
{
    int i, b[6];

    //如果当前是1、2、12位置，因为已经填充，所以直接填充下一个位置
    if(x==1 || x==2 || x==12){
        dfs(x+1);
        return;
    }

    // 填充完一个组合
    if(x == 13){        
        b[0] = g_array[1]+g_array[3]+g_array[6]+g_array[8]; 
        b[1] = g_array[1]+g_array[4]+g_array[7]+g_array[11];
        b[2] = g_array[2]+g_array[3]+g_array[4]+g_array[5];
        b[3] = g_array[2]+g_array[6]+g_array[9]+g_array[12];
        b[4] = g_array[5]+g_array[7]+g_array[10]+g_array[12];
        b[5] = g_array[8]+g_array[9]+g_array[10]+g_array[11];
        
        for(i=1; i<6; i++){
            if(b[i] != b[i-1]){
                break;
            }
        }

        if(i == 6)
            printf("result:%d\n", g_array[6]); 
    }
        
    for(i=1;i<13;i++){
        if(g_value[i]==0){    
            g_value[i] = 1;    

            //填充一个位置后，递归尝试后面的所有组合
            g_array[x] = i; 
            dfs(x+1);
            g_value[i] = 0;    
        }        
    }
}

int main()
{
    int i;
    g_array[1] = 1;
    g_array[2] = 8;
    g_array[12] = 3;
    g_value[1] = 1;
    g_value[8] = 1;
    g_value[3] = 1;
    dfs(1);       
    return 0;
}