Python 实现简单的感知机算法
感知机
随机生成一些点和一条原始直线,然后用感知机算法来生成一条直线进行分类,比较差别
导入包并设定画图尺寸
import numpy as np import matplotlib.pyplot as plt %matplotlib inline plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 plt.rcParams['figure.figsize'] = (8.0,6.0) # 生成图的大小
随机产生数据
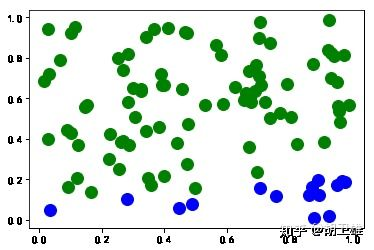
fig = plt.figure() # 产生新画布 figa = plt.gca() # 获取当前画布 # 产生100个点 N = 100 xn = np.random.rand(N,2) x = np.linspace(0,1) # linspace函数可以生成元素为50的等差数列 # 随机生成一条直线 a = np.random.rand() b = np.random.rand() f = lambda x:a*x+b # 线性分割前面产生的点 yn = np.zeros([N,1]) for i in range(N): if(f(xn[i,0])>=xn[i,1]): yn[i] = 1 plt.plot(xn[i,0],xn[i,1],'bo',markersize=12) # 'bo':用蓝色圆圈标记 if(f(xn[i,0])<xn[i,1]): yn[i] = -1 plt.plot(xn[i,0],xn[i,1],'go',markersize=12) # 'go':用绿色圆圈标记
超平面的实现
def perceptron(xn,yn,MaxIter=1000,a=0.1,w=np.zeros(3)): ''' 实现一个二维感知机 对于给定的(x,y),感知机将通过迭代寻找最佳的超平面来进行分类 输入: xn:数据点 N*2 向量 yn:分类结果 N*1 向量 MaxIter:最大迭代次数(可选参数) a:学习率(可选参数) w:初始值(可选参数) 输出: w:超平面参数使得 y=ax+b 最好地分割平面 注意: 由于初始值为随机选取,因此迭代到收敛可能需要一点时间 该函数仅为感知机的简单实现,实际需要考虑更多的内容 ''' N = xn.shape[0] # 生成超平面 f = lambda x:np.sign(w[0]*1+w[1]*x[0]+w[2]*x[1]) # 反向传播 for _ in range(MaxIter): i = np.random.randint(N) if(yn[i]!=f(xn[i,:])): w[0] = w[0] + yn[i]*a*1 w[1] = w[1] + yn[i]*a*xn[i,0] w[2] = w[2] + yn[i]*a*xn[i,1] return w
实际应用
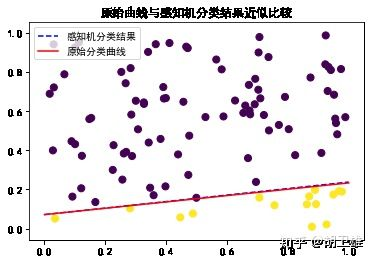
w = perceptron(xn,yn) # 利用权重w,计算 y=ax+b 中的a,b new_b = -w[0] / w[2] new_a = -w[1] / w[2] y = lambda x:new_a*x+new_b # 分割颜色 sep_color = (yn) / 2.0 plt.figure() figa = plt.gca() plt.scatter(xn[:,0],xn[:,1],c=sep_color.flatten(),s=50) # s:表示点的大小 plt.plot(x,y(x),'b--',label='感知机分类结果') plt.plot(x,f(x),'r',label='原始分类曲线') plt.legend() plt.title('原始曲线与感知机分类结果近似比较') Text(0.5, 1.0, '原始曲线与感知机分类结果近似比较')