数据结构与算法笔记(一) 程序性能分析
程序性能：一个程序对内存和时间的需要。要对数据结构和算法给予评价，就必须能够计算程序性能
1. 用操作数和执行步数估计程序的运行时间
2. 用符号法描述程序在最好，最坏，平均情况下的运行时间。
确定程序性能： 分析方法， 实验方法
知道两个概念：
空间复杂度：程序运行时所需的内存空间的大小
时间复杂度：运行程序所需要的时间
空间复杂度的组成：
1.指令空间：编译之后的程序指令所需要的存储空间
2.数据空间： 所有常量和变量所需要的存储空间
3.环境栈空间：环境栈用来保存暂停的函数和方法在恢复运行时所需要的信息。
任意程序所需要的空间可以表示为： c+S， 其中c是固定部分，S是可变部分
实例分析: 递归函数实现n个元素所有排列的输出
例子：
顺序查找（非递归）
template<typename T>
int sequenceSearch(T list[], int n, const T& key)
{
// list[] 查找的列表， n列表长度， key查找的元素
for(int i=0; i<n && list[i]!=key; i++); // 注意这里的写法，将判断条件直接放到for里面
if(i==n) return -1;
else return i; //返回index
}这个程序的空间复杂度： S=0， （需要的参数已经在函数外定义） int i; 呢
顺序查找（递归）
template<typename T>
int sequenceSearch(T list[], int n, const T& key)
{
// list[] 查找的列表， n列表长度， key查找的元素
if(n<1) return -1; // 停止条件
if(list[n-1]==key) return n-1; // 满足匹配条件
sequenceSearch(list, n-1, key); // 递归调用
}空间复杂度： 递归的深度为：max{n, 1},每次递归栈需要保存返回地址(4字节)， S = 4*max{n,1}
时间复杂度：
程序需要的时间T:
T = 编译时间 + 运行时间
主要关注运行时间Tp(n), n为问题的实例特征
计数操作：
选择一种或多种关键操作（+-*/），确定每一种操作进行的次数
例如：
多项式求和: P(x)=C0+C1*X+C2*X^2+...Cn*X^n // 按照常规方法
template<typename T>
T polyEval(T coeff[], int n, const T& x)
{
// coeff 多项式系数 n多项式阶数 x取值
T y = 1;
T value = coeff[0];
for(int i=0; i<n; i++)
{
y = y*x;
value = value + y*coeff[i];
}
return value;
}时间复杂度：在n次的for循环中，每次进行2次乘法和一次加法，总共进行2n次乘法和n次加法。
Horner分解多项式计算：
P(x) = 5*x^3-4*x^2+x+7=((5*x-4)*x+1)*x+7;
template<typename T>
T polyEval(T coeff[], int n, const T& x)
{
// horner法则分解多项式
// coeff 多项式系数[a0,a1,a2...an] n多项式阶数 x取值
T value = coeff[n];
for(int i=1; i<=n; i++)
{
value = value*x + coeff[n-i];
}
return value;
}时间复杂度：在n次的for循环中，每次进行1次乘法和1次加法，总共进行n次乘法和n次加法。因此这种方法计算多项式更快
元素在序列中的名次计算：
【4，3，9，3，9】一个元素的名词等于比它小的元素的个数加它左边出现的与它相同的元素个数
template<typename T>
int rank(T a[], int n, T r[])
{
// 结果早r[]中返回
for(int i=0; i<n; i++)
{
r[i] = 0; // 初始化
}
for(int i=1; i<n; i++)
{
for(int j=0; j<i; j++) // 注有这里的实现方法；
{
if(a[i]>=a[j]) r[i]++;
else r[j]++;
}
}
}计数排序：在得到r[ ]数组的基础上，对a进行排序
template<typename T>
int rank(T a[], int n, T r[])
{
// 结果早r[]中返回
for(int i=0; i<n; i++)
{
r[i] = 0; // 初始化
}
for(int i=1; i<n; i++)
{
for(int j=0; j<i; j++) // 注有这里的实现方法；
{
if(a[i]>=a[j]) r[i]++;
else r[j]++;
}
}
*u = new T [n];
for(int i=0; i<n; i++)
{
u[r[i]] = a[i];
}
// 把u中的数组放回a中
for(int i=0; i<n; i++)
{
a[i] = u[i];
}
delete [] u; // 删除为u分配的内存
}冒泡排序bulbSort
一次冒泡的过程，数列的最大元素一定会移动到数列的尾部，这与选择排序中寻找序列最大值并将其放到队尾的操作一致，接着对前n-1个元素进行相同的操作：
#include <iostream>
#include <string>
using namespace std;
template<typename T>
void bulbSort(T list[], int n)
{
for(int i=n; i>0; i--) // 对前i个元素进行操作
{
for(int j=0; j<i-1; j++) // 一次冒泡过程
{
if(list[j]>list[j+1]) // 冒泡
{
T temp = list[j+1];
list[j+1] = list[j];
list[j] = temp;
}
}
}
}
int main(int argc, char *argv[])
{
cout << "Hello" << endl;
int a[] = {1,5,2,9,5,6,4,3};
// selectSort(a, 8);
bulbSort(a, 8);
for(int i=0; i<8; i++)
{
cout << a[i] << " ";
}
cout << endl;
return 0;
}
运行结果：
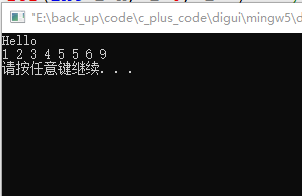
一次冒泡如果有n个元素，则需要n-1次的比较，n次冒泡一共需要比较的次数是：1+2+3...+(n-1)=n(n-1)/2
最好最坏和平均操作技术
因为操作技术并不一定单纯是问题的规模n的函数，例如bulbSort()函数，一次冒泡进行比较的次数与数组的整体值有关，交换次数可能在0到(n-1)之间。 平均操作技计数不好确定，集中分析最好和最坏操作计数。
例如:
在有序数组中插入元素：从数组右侧开始一次进行比较
template<typename T>
void insert(T list[], int& n, T key)
{
// 假设数组a的容量大于n
for(int i=n-1; i>=0&&list[i]>=key; i--) // 注意这的条件
a[i+1] = a[i];
a[i+1] = key;
n++; // 数组a增加一个元素
}分析比较次数 ： 平均比较次数n/2 + n/(n+1)
在上面的选择排序中，如果序列已经是有序的，程序还是会进行比较，为了避免不必要的比较，可以在每次寻找最大元素的时候，检查序列是否有序：
#include <iostream>
#include <string>
using namespace std;
template<typename T>
void selectSort(T list[], int n)
{
bool sorted=false; // 序列检查标志位
for(int size=n; size>1&&!sorted; size--)
{
int indexOfmax = 0;
sorted = true;
for(int i=1; i<size; i++)
{
if(list[indexOfmax]<=list[i])
indexOfmax = i;
else
sorted = false; // 避免对有序的序列还进行比较
}
T temp = list[indexOfmax];
list[indexOfmax] = list[size-1];
list[size-1] = temp;
}
}
int main(int argc, char *argv[])
{
cout << "Hello" << endl;
int a[] = {1,5,2,9,5,6,4,3};
// selectSort(a, 8);
selectSort(a, 8);
for(int i=0; i<8; i++)
{
cout << a[i] << " ";
}
cout << endl;
return 0;
}
步数：
上面的操作计数中使用特定操作的计数来估算程序的时间复杂度。而在步数（step-count）中，将对程序的所有操作部分都进行统计。
一步（a step）是一个计算单位，他独立于选定的实例特征。
一个程序步： 可以定义为一个语法或者语义上的程序片段，该片段的执行时间独立于时间特征。
不是可以告诉我们随着实例特征的变化，程序的执行时间是如何变化的。
重点：学会剖析法分析程序的步数！
-------------------------------------------------------------------------------------------------------
当实例特征n很大的时候，需要使用渐进记法。
1. 了解各种记法
1 常量
logn 对数
n 线性
nlogn n倍对数
n^2 平方
n^3 立方
2^n 指数
n! 阶乘
大小顺序：
1 < longn < n < nlogn < n^2 < n^3 < 2^n < n!
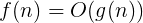
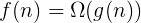
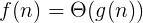
时间复杂度实际上是衡量执行时间的变化趋势(变化率)，当输入规模n趋于大规模时，执行时间的变化趋势。
--------------------------------------------------------------------------------
性能测量
程序的性能不仅依赖操作类型和数量，而且依赖数据和指令的内存模式。
计算机内存有等级之分，如L1高速缓存，L2高速缓存，主存。内存时间不同，访问模式也就不同
性能测量关注的是一个程序实际需要的时间和空间。
运行空间：
1.指令空间和静态分配的数据空间由编译器编译时确定，大小可以用操作系统指令得到。
2.递归栈空间和动态分配的空间可以通过分析的方法计算
测量运行时间，需要一个定时机制：可以使用c++函数clock()函数来测量，在头文件time.h中定义了常数CLOCK_PER_SEC,记录每秒流逝的 “滴答“ 数，并转换成秒数。CLOCK_PER_SEC=1000， 滴答一次等于一毫秒
选择排序程序：
#include <iostream>
#include <string>
#include <time.h>
using namespace std;
template<typename T>
void insertionSort(T list[], int n) // 注意选择排序的思路
{
for(int i=1; i<n; i++) // 从a[i]（i=1；i<n）开始，向前遍历
{
T temp = list[i]; // a[i]插入a[0: i-1]
int j;
for(j=i-1; j>=0&&temp<list[j]; j--) // 数组元素后移
{
list[j+1] = list[j];
}
list[j+1] = temp; // list[j+1]
}
}
int main(int argc, char *argv[])
{
int a[1000], step = 10;
cout << "The worst case time , in mill-second is " << endl;
cout << endl << "Time" << endl;
double clock_per_sec = static_cast<double>(CLOCKS_PER_SEC);
for(int n=0; n<=1000; n+=step)
{
// 用最坏测试数据初始化
long int numberOfRepeat = 0;
clock_t start_time = clock();
do
{
for(int k=0; k<n; k++)
{
a[k] = n-k;
}
insertionSort(a, n);
numberOfRepeat++;
}while(clock()-start_time<1000);
double elapsee_time = (clock() - start_time)/clock_per_sec;
cout << n << '\t' << numberOfRepeat << '\t' << elapsee_time/numberOfRepeat*1000 << endl;
if(n==100) step = 100;
}
return 0;
}
测量的结果：
因为执行一次对于clock()来说时间太短，不便于测量，所以需要执行多次才能够进行测量
