数据结构与算法笔记(三) 线性表(链式描述) 链表
在链式描述中,线性表元素的位置在内存中是随机的,每个元素都有一个明确的指针指向线性表的下一个元素的位置。
1.单向链表:
数据对象的每一个元素都用一个单元或者节点来描述,每个节点都明确包含另一个相关节点的位置信息。
线性表的链式描述图如下所示:

每个节点只有一个链,这种结构称为单向链表
重点: 链表的插入与删除
结构chainNode,数据成员element是节点的数据域,存储线性表的元素,数据成员next是节点的链域,存储下一个节点的指针。
定义链表类chain:
首先定义链表的节点的数据结构,结构体chainNode;
template<typename T>
struct chainNode // 定义节点的数据结构
{
// 数据成员
T element; // 数据域
chainNode<T>* next; // 指针域
//chainNode() {}
chainNode(T& element) // 结构体的构造函数
{
this->element = element;
}
chainNode(T& element, chainNode<T>* next) // 结构体的构造函数
{
this->element = element; // 这里的this的作用类似于类里面的this
this->next = next;
}
};链表类chain的定义:
template<typename T>
class chain: public linearList<T>
{
protected:
bool checkIndex(int theIndex) const; // 索引是否有效
chainNode<T>* firstNode;
int listSize;
public:
chain(int init_capacity=10);
chain(const chain<T>&); // 拷贝构造函数
~chain(); // 析构函数
//抽象数据类型ADT
bool empty() const;
int size() const;
T& get(int index);
int indexOf(T& element) const;
void erase(int index);
void insert(int index);
void output() const;
};重点掌握的,链表的拷贝构造函数实现,析构函数实现,插入函数和删除函数
拷贝构造函数:
template<typename T>
chain<T>::chain(const chain<T>& new_chain) // 重要
{
listSize = new_chain.listSize;
if(listSize==0) // 要复制的链表为空
{
firstNode = NULL;
return; // end
}
// 链表非空
chainNode<T>* sourceNode = new_chain.firstNode;
firstNode = new chainNode<T>(sourceNode->element); // 结构体变量的初始化 chainNode结构体有两个构造方法,这是其中的一个
// firstNode = new chainNode<T>((*sourceNode).element) //解引用
sourceNode = sourceNode->next; // 原来链表的指针
chainNode<T>* targetNode = firstNode; // 复制得到的链表的节点指针
while(sourceNode!=NULL)
{
targetNode->next = new chainNode<T>(sourceNode->element);
targetNode = targetNode->next;
sourceNode = sourceNode->next;
}
targetNode->next = NULL; // 链表结束
}指针移动细节如下图所示:
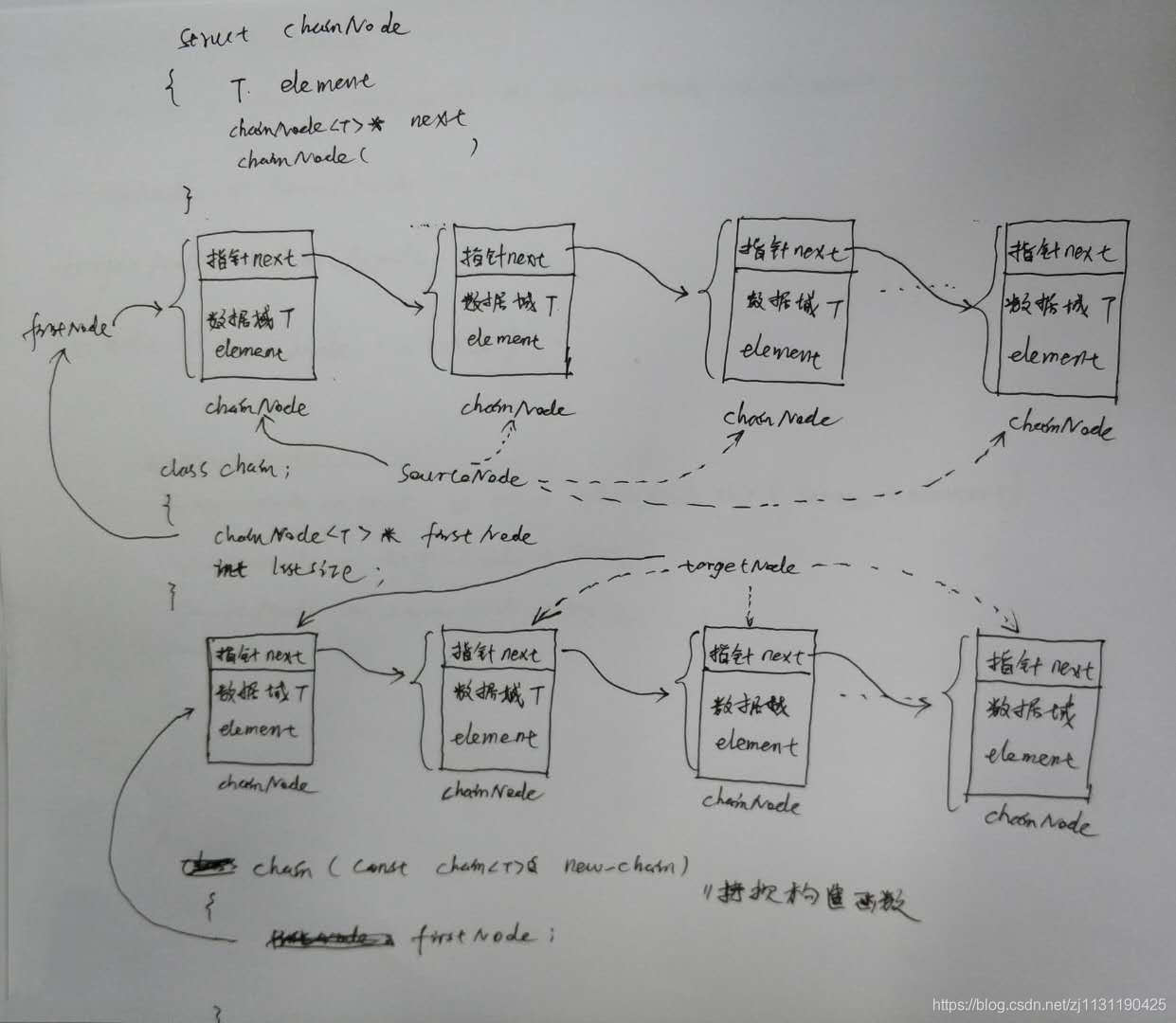
析构函数:
析构函数逐个删除链表的节点,通过重复清除链表的首个元素节点,知道链表为空。在清除之前用变量保存第二个元素节点的指针。时间复杂度
template<typename T>
chain<T>::~chain()
{
// 链表的析构函数, 删除链表的所有节点
while(firstNode!=NULL)
{
chainNode<T>* nextNode = firstNode->next; // 保存链表第二个节点的指针
delete firstNode; // 删除释放第一个节点的内存
firstNode = nextNode; // 将第二个节点变为第一个节点
}
}
链表类chain的完整代码:
1. chain的基类, 抽象类linearList
#ifndef LINEAR_LIST_H
#define LINEAR_LIST_H
#include <iostream>
using namespace std;
template<typename T> // 定义一个抽象类
class linearList
{
public:
// 抽象类中的纯虚函数
virtual ~linearList() {}; // 析构函数
virtual bool empty() const=0;
virtual int size() const=0;
virtual T& get(int index) const=0;
virtual int indexOf(const T x) const=0; // 这里定义的是虚函数,虚函数virtual functiuonName() const=0表示的是定义为纯虚函数,这个纯虚函数是只读函数
virtual void erase(int index) = 0; // 这里定义的是虚函数,虚函数virtual functiuonName()=0表示的是定义为纯虚函数,这个纯虚函数不是只读函数
virtual void insert(int index, T x) = 0;
// virtual void output(ostream& out) const=0;
};
#endif
2. 类chain的定义和实现:
#ifndef CHAIN_H
#define CHAIN_H
#include <iostream>
#include "E:\back_up\code\c_plus_code\digui\external_file\linearlist.h"
template<typename T>
struct chainNode // 定义节点的数据结构
{
// 数据成员
T element; // 数据域
chainNode<T>* next; // 指针域
//chainNode() {}
chainNode(T& element) // 结构体的构造函数
{
this->element = element;
}
chainNode(T& element, chainNode<T>* next) // 结构体的构造函数
{
this->element = element; // 这里的this的作用类似于类里面的this
this->next = next;
}
};
template<typename T>
class chain: public linearList<T>
{
protected:
//bool checkIndex(int theIndex) const; // 索引是否有效
chainNode<T>* firstNode;
int listSize;
public:
chain(int init_capacity=10);
chain(const chain<T>& new_chain); // 拷贝构造函数
~chain(); // 析构函数
//抽象数据类型ADT
bool empty() const;
int size() const;
T& get(int index) const;
int indexOf(T x) const;
void erase(int index);
void insert(int index, T x);
void output() const;
};
/*
template<typename T>
bool chain<T>::checkIndex(int index)
{
return (index>=0&&index<=listSize)?true:false;
}
*/
template<typename T>
chain<T>::chain(int init_capacity) // 构造函数
{
if(init_capacity<1)
cout << "Init capacity should be greater than 0" << endl;
firstNode = NULL; // 链表初始化
listSize = 0;
}
#endif
template<typename T>
chain<T>::chain(const chain<T>& new_chain) // 重要
{
listSize = new_chain.listSize;
if(listSize==0) // 要复制的链表为空
{
firstNode = NULL;
return; // end
}
// 链表非空
chainNode<T>* sourceNode = new_chain.firstNode;
firstNode = new chainNode<T>(sourceNode->element); // 结构体变量的初始化 chainNode结构体有两个构造方法,这是其中的一个
// firstNode = new chainNode<T>((*sourceNode).element) //解引用
sourceNode = sourceNode->next; // 原来链表的指针
chainNode<T>* targetNode = firstNode; // 复制得到的链表的节点指针
while(sourceNode!=NULL)
{
targetNode->next = new chainNode<T>(sourceNode->element);
targetNode = targetNode->next;
sourceNode = sourceNode->next;
}
targetNode->next = NULL; // 链表结束
}
template<typename T>
chain<T>::~chain()
{
// 链表的析构函数, 删除链表的所有节点
while(firstNode!=NULL)
{
chainNode<T>* nextNode = firstNode->next; // 保存链表第二个节点的指针
delete firstNode; // 删除释放第一个节点的内存
firstNode = nextNode; // 将第二个节点变为第一个节点
}
}
template<typename T>
bool chain<T>::empty() const
{
return listSize==0;
}
template<typename T>
int chain<T>::size() const
{
return listSize;
}
template<typename T>
T& chain<T>::get(int index) const
{
/*
if(checkIndex(index))
{
chainNode<T>* currentNode = firstNode;
for(int i=0; i<index; i++)
{
currentNode = currentNode->next; //先找到index的前一个节点
}
return currentNode->element;
}
else
{
cout << "The index is invalid" << endl;
}
*/
chainNode<T>* currentNode = firstNode;
for(int i=0; i<index; i++)
{
currentNode = currentNode->next; //先找到index的前一个节点
}
return currentNode->element;
}
template<typename T>
int chain<T>::indexOf(T the_element) const
{
// 返回the_element首次出现的索引值
// fouzefanhui -1
chainNode<T>* currentNode = firstNode;
int index_cnt = 0;
while(currentNode!=NULL)
{
if(currentNode->element == the_element)
{
return index_cnt;
}
currentNode = currentNode->next;
index_cnt ++;
}
return -1;
}
template<typename T>
void chain<T>::insert(int index, T x)
{
// 在链表中插入元素
//chainNode<T>* currentNode = firstNode;
// 插入元素得考虑是否在表头插入;
if(index==0) // 在表头插入
{
firstNode = new chainNode<T>(x, firstNode); // 造结构体构造方法
//firstNode->next = currentNode;
}
else // 不是在表头插入
{
chainNode<T>* currentNode = firstNode;
for(int i=0; i<index-1; i++)
{
currentNode = currentNode->next;
}
currentNode->next = new chainNode<T>(x, currentNode->next); // 插入元素到链表index位置
}
listSize++;
}
template<typename T>
void chain<T>::erase(int index)
{
// 1.检查index的合法性
// 2.检查index==0
if(index==0)
{
chainNode<T>* currentNode = firstNode;
firstNode = firstNode->next;
delete currentNode;
listSize--;
}
else
{
chainNode<T>* currentNode = firstNode;
// int node_cnt = 0;
for(int i=0; i<index-1; i++)
{
currentNode = currentNode->next;
}
// currentNode 指向第index-1个节点
chainNode<T>* tmp = currentNode->next; // tmp指向第index个节点
currentNode->next = tmp->next;
delete tmp;
listSize--;
}
}
template<typename T>
void chain<T>::output() const
{
chainNode<T>* currentNode = firstNode;
int node_cnt = 0;
while(currentNode!=NULL) //遍历链表的所有元素
{
cout << currentNode->element << " ";
if((node_cnt+1)%10==0)
{
cout << endl;
}
currentNode = currentNode->next;
node_cnt++;
}
}
3。测试函数:
main.cpp
#include <iostream>
#include <string>
#include <time.h>
#include "E:\back_up\code\c_plus_code\digui\external_file\linearlist.h"
#include "E:\back_up\code\c_plus_code\digui\external_file\arraylist.h"
#include "E:\back_up\code\c_plus_code\digui\external_file\chain.h"
using namespace std;
// 实现友元函数
int main(int argc, char *argv[])
{
/*
arrayList<double> array(3);
for(int i=0; i<10; i++)
{
array.insert(i, i);
}
//array.insert(0, a);
//array.insert(1, b);
array.output();
array.insert(9, 9.9);
array.output();
*/
chain<int> chain_1;
for(int i=0; i<10; i++)
{
chain_1.insert(i, i*i);
}
cout << "The size of chain is " << chain_1.size() << endl;
chain_1.output();
// cout << "The size of chain is " << chain_1.get() << endl;
chain_1.insert(3, 520);
cout << "The size of chain is " << chain_1.size() << endl;
chain_1.output();
chain_1.erase(9);
cout << "The size of chain is " << chain_1.size() << endl;
chain_1.output();
cout << "The " << 3 << " element in chain is " << chain_1.get(3) << endl;
return 0;
}
测试结果: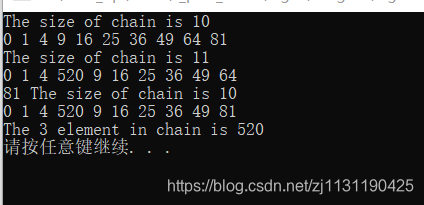
------------------------------------------------------------------------------------------------
给类chain添加clea()功能:
template<typename T>
void chain<T>::clear()
{
while(firstNode!=NULL)
{
chainNode<T>* nextNode = firstNode->next;
delete firstNode;
firstNode = nextNode;
}
listSize = 0;
}main.cpp
#include <iostream>
#include <string>
#include <time.h>
#include "E:\back_up\code\c_plus_code\digui\external_file\linearlist.h"
#include "E:\back_up\code\c_plus_code\digui\external_file\arraylist.h"
#include "E:\back_up\code\c_plus_code\digui\external_file\chain.h"
using namespace std;
// 实现友元函数
int main(int argc, char *argv[])
{
/*
arrayList<double> array(3);
for(int i=0; i<10; i++)
{
array.insert(i, i);
}
//array.insert(0, a);
//array.insert(1, b);
array.output();
array.insert(9, 9.9);
array.output();
*/
chain<int> chain_1;
for(int i=0; i<10; i++)
{
chain_1.insert(i, i*i);
}
cout << "The size of chain is " << chain_1.size() << endl;
chain_1.output();
chain_1.clear();
if(chain_1.empty())
{
cout << "The chain is empty" << endl;
}
else
{
cout << "The chain is not empty" << endl;
}
return 0;
}
测试结果:
性能比较:
1.内存比较:
在数组描述的线性表中,数组满的时候,数组的长度需要加倍,,当线性表的元素个数不及数组长度的1/4时,数组元素减半。
n个元素的线性表可以存储在n~4n长度的数组中。 假设每个元素需要s个字节,则所占的空间为ns~4ns.对于链表,n个元素分配n个节点,每个指针4字节大小,则所占的空间的小为n(s+4),因此在选择线性表的描述方法时,空间上的差异不是决定因素。
2.时间比较
例如get(int index)操作,链表的时间复杂度是 ,数组的时间复杂度是
,其他操作的时间如下:
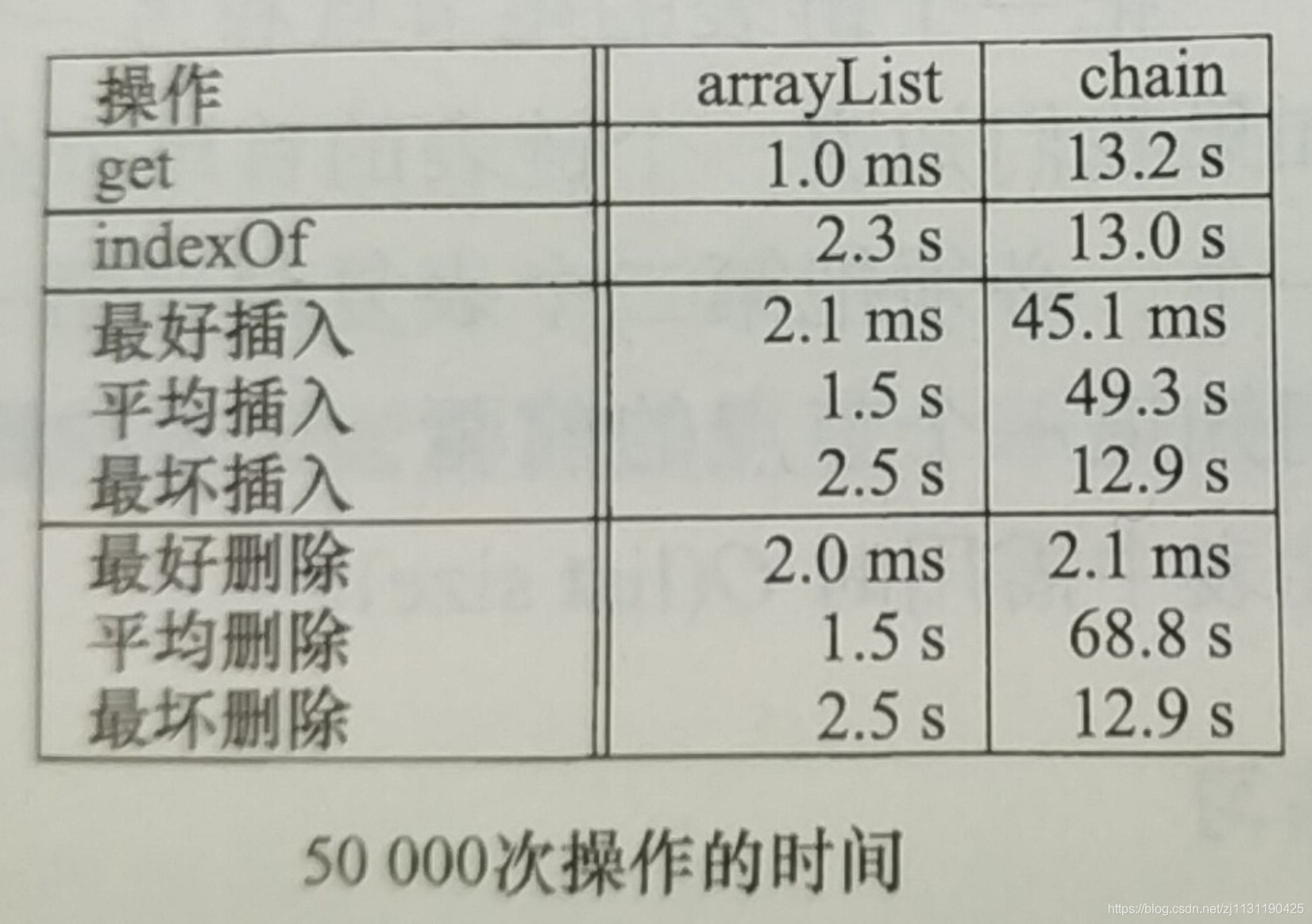
--------------------------------------------------f分割线--------------------------------------------------------
给链表添加一些新的方法
1.实现 setSize()方法:



