数据结构与算法笔记（五） 链表的应用

1.箱子排序：

假设：

用链表保存一个班级学生的清单，节点的数据域包括：姓名，社会保险号码，作业和考试的分数，所有作业和加权的总分。假设分数介于(0-100)之间，按照总分对学生进行排序，一种较快的排序方法是箱子排序(bin sort)：把相同分数的节点放到一个箱子里，然后把箱子连接起来就得到有序的链表

箱子排序要做的是:(1)逐个删除输入链表的节点，把删除的节点分配到相应的箱子中9,每个箱子相当于一个链表  (2)把每个箱子中的链表收集起来并连接，使其成为一个有序的链表

定义学生记录：

struct studentRecord
{
	int score;
    string name;
    
    // 构造方法
	studentRecord(const string& name, int score)
	{
		this->name = name;
		this->score = score;
	} 
	
    int operator !=(const studentRecord& x) const
    {
		return score==x.score;
	}
	
	operator int() const
	{
		return score;
	}
	
};

凸包：

多边形：至少有三条直线便的平面封闭图形，多边形包含边线上的点，也包含变现内的点。多边形的任意两个点的连线都不包含多边形以内的点，则称为凸多边形.

一个平面点集S的凸包：包含点集S的最小凸多边形

多边形的定点称为S的极点。

寻找平面点集S的凸包的算法：

1.处理退化情况

S的点数少于3;

S的所有点在同一条直线上， 返回包含S的所有点的最短直线的定点

2. 极角排序：

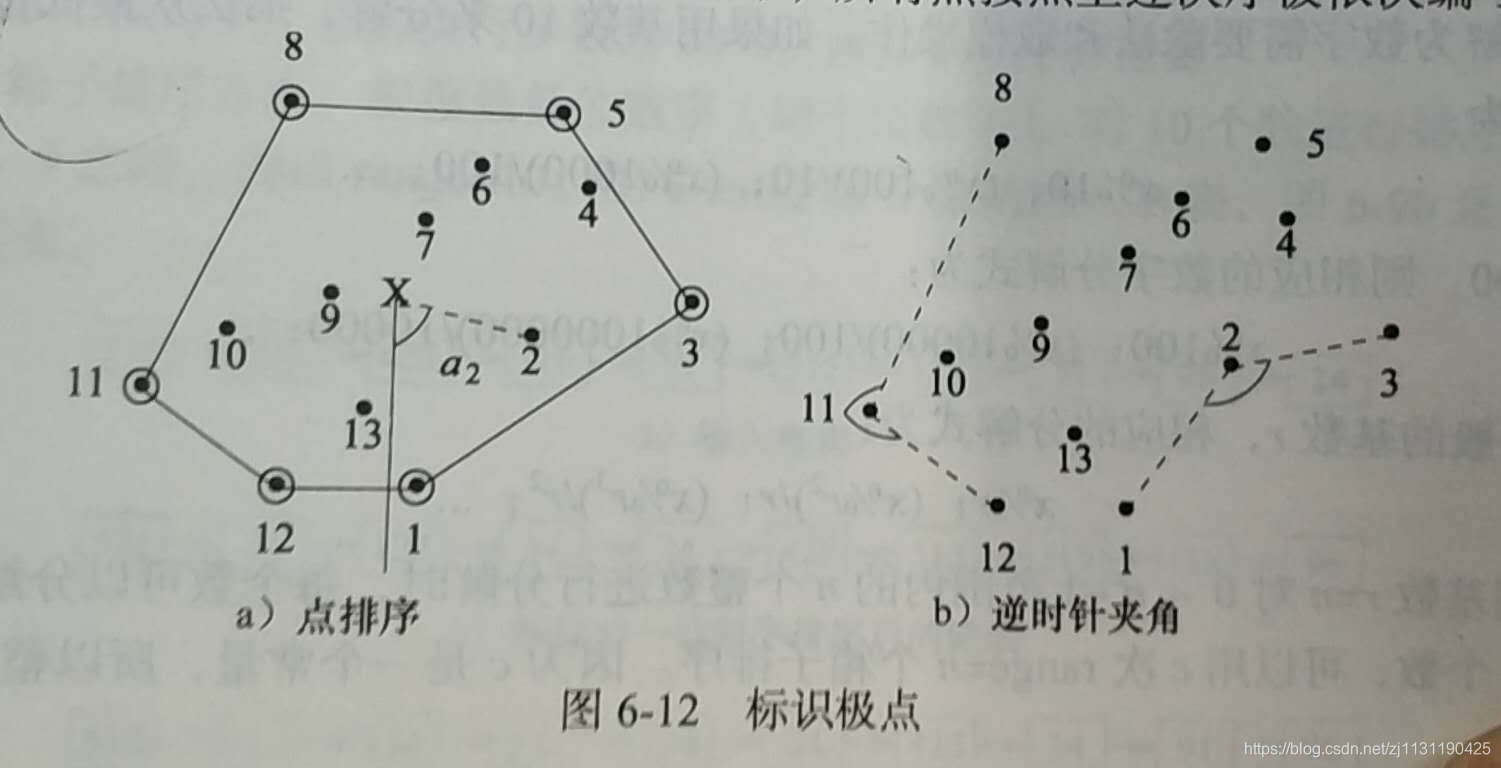
假定在S的凸包内取一点X, 从X向下画垂线。垂线和X到点s_i之间的连线有一个夹角，称为极角。

按照极角的递增次序排列S的点，如果极角相同，则按照与X的距离递增来排列S的点。

3.寻找并删除非极点的点

如果u,v,w是按照逆时针排列的三个连续的极点，从u->v,w->v之间的连线的夹角应该大于180，当按照极角排列的三个点的极角小于等于180时，则第二个点不是极点，可以将其删除。因为当按照逆时针方向在一个凸多边形上行走时，所有的转弯都是向左转。

采用双向循环链表存储数据

假设p时链表中的点（y坐标最小或者x坐标最大, 因为这个点肯定在凸包上）：

for(x=p, rx=x->right; p!=rx)
{
     rrx = rx->right;
     if(invalid(x,rx,rrx))    // 三个点不满足条件， 删除rx
     {
          rx = x;
          x = rx;
     }
     else
     {
          x = rx;
          rx = rrx;
     }
}

---------------------------------------------------分割线-----------------------------------------------