c++中大矩阵乘法计算的效率问题
假设两个大小相同的方阵需要计算乘法：按照矩阵乘法的规则：
先写一段矩阵初始化代码：
#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;
void matrix_print(int **a, int n);
int main(int argc, char *argv[])
{
// 定义数组：
srand(time(0));
int matrix_n = 10;
int numberOfRows = matrix_n;
int numberOfCols = matrix_n;
int** mat1 = new int* [numberOfRows]; // a矩阵的行数
int** mat2 = new int* [numberOfRows];
int** mat3 = new int* [numberOfRows];
for(int i=0; i<numberOfRows; i++)
{
mat1[i] = new int[numberOfCols];
mat2[i] = new int[numberOfCols];
mat3[i] = new int[numberOfCols];
}
// 初始化矩阵 1-10之间的随机数
for(int i=0; i<numberOfRows; i++)
{
for(int j=0; j<numberOfCols; j++)
{
mat1[i][j] = 1 + rand()%(10-1+1);
mat2[i][j] = 1 + rand()%(10-1+1);
}
}
matrix_print(mat1, matrix_n); // 输出矩阵
matrix_print(mat2, matrix_n); // 输出矩阵
//matrix_print(mat3, matrix_n);
return 0;
}
// 输出矩阵
void matrix_print(int **a, int n)
{
for(int i=0; i<n; i++)
{
for(int j=0; j<n; j++)
{
cout << a[i][j] << " ";
}
cout << endl;
}
cout << endl;
}
初步测试：
现在将矩阵乘法的循环的潜逃次序改变一下，改写为一个新的函数，两个函数对比如下：
1.matrix_multiply_ijk版本：
// 计算矩阵乘法 ijk
void matrix_multiply_ijk(int **a, int **b, int **c, int n) // n表示方阵的阶数
{
for(int i=0; i<n; i++)
{
for(int j=0; j<n; j++)
{
int sum = 0;
for(int k=0; k<n; k++)
{
sum += a[i][k]*b[k][j];
}
c[i][j] = sum;
}
}
}
2.matrix_multiply_ikj版本：
// 计算矩阵乘法 ikj
void matrix_multiply_ikj(int **a, int **b, int **c, int n) // n表示方阵的阶数
{
for(int i=0; i<n; i++)
{
for(int k=0; k<n; k++)
{
int sum = 0;
int j;
for(j=0; j<n; j++)
{
sum += a[i][k]*b[k][j];
}
c[i][j] = sum;
}
}
}性能测量：
3.通过在不同的维度下测试两个函数的运行时间：
c++测试代码运行时间的方法：通过像个的时钟数来测量；
在ijk的方法下：
| 1st | 2nd | 3rd | 4th | |
| n=100 | 6 | 3 | 7 | 4 |
| n=300 | 104 | 90 | 95 | 92 |
| n=500 | 474 | 492 | 484 | 469 |
| n=800 | 2001 | 2100 | 2170 | 2042 |
| n=1200 | 10615 | 9821 | 9689 | 9703 |
| n=2000 | 63677 | 62797 | 62698 | 62551 |
在ikj的方法下：
| 1st | 2nd | 3rd | 4th | |
| n=100 | 5 | 3 | 3 | 3 |
| n=300 | 77 | 79 | 81 | 78 |
| n=500 | 328 | 351 | 341 | 359 |
| n=800 | 1435 | 1413 | 1423 | 1453 |
| n=1200 | 4901 | 4778 | 4849 | 4694 |
| n=2000 | 21664 | 21501 | 21968 | 21947 |
结论：
可以看到。在ikj的方案下，矩阵乘法的运算速度较快，而且在矩阵阶数n越大的时候，这种差别越是明显。在计算矩阵乘法的过程中，三层的循环嵌套共有六种排列方式，虽然在每种嵌套方式下，都要执行同样数量的操作，但是花费的时间是不同的。这是因为在不同的嵌套方式下，改变了数据的访问模式，进而改变了缓存未命中的数量。最终影响了运行时间。
关于缓存未命中的简单理解：
简单计算机模型：
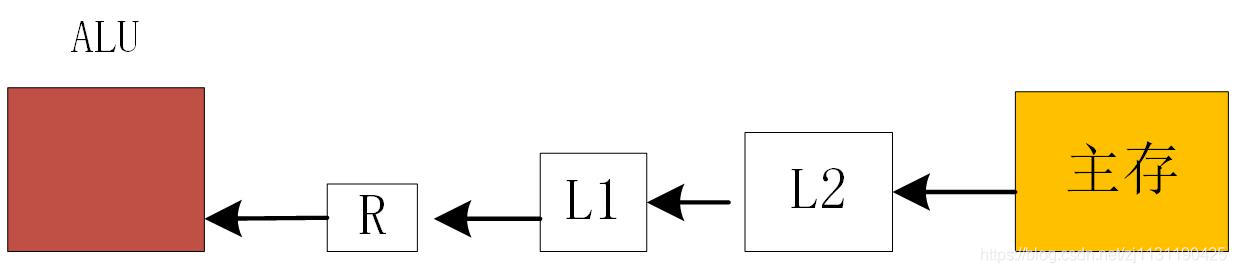
L1 一级缓存
L2二级缓存
R 寄存器
ALU算术逻辑单元
在程序开始运行时，数据都位于主存中，需要将参与运算的数据从主存移到寄存器再进行运算。如果需要的数据没有在一级缓存，而是在二级缓存，而需要将数据存二级缓存移动到一级缓存，这称为一级缓存未命中，当需要的数据没有在二级缓存中时，此时为二级缓存未命中，则需要将数据从主存移动到二级缓存，再移动到一级缓存。所以可以通过减少缓存未命中的数量，提高程序的运行效率。计算机会采取相应的策略。
完整代码：
#include <iostream>
#include <cstdlib>
#include <ctime>
#include <time.h> // 包含时间测量的函数
using namespace std;
void matrix_multiply_ijk(int **a, int **b, int **c, int n);
void matrix_multiply_ikj(int **a, int **b, int **c, int n);
void matrix_print(int **a, int n);
int main(int argc, char *argv[])
{
// 定义数组：
srand(time(0));
int matrix_n = 2000; // 修改矩阵的阶数为不同的值
int numberOfRows = matrix_n;
int numberOfCols = matrix_n;
int** mat1 = new int* [numberOfRows]; // a矩阵的行数
int** mat2 = new int* [numberOfRows];
int** mat3 = new int* [numberOfRows];
for(int i=0; i<numberOfRows; i++)
{
mat1[i] = new int[numberOfCols];
mat2[i] = new int[numberOfCols];
mat3[i] = new int[numberOfCols];
}
// 初始化矩阵 1-10之间的随机数
for(int i=0; i<numberOfRows; i++)
{
for(int j=0; j<numberOfCols; j++)
{
mat1[i][j] = 1 + rand()%(10-1+1);
mat2[i][j] = 1 + rand()%(10-1+1);
}
}
//matrix_print(mat1, matrix_n); // 输出矩阵
//matrix_print(mat2, matrix_n); // 输出矩阵
//matrix_print(mat3, matrix_n);
double clocks_PerMills = double(CLOCKS_PER_SEC) / 1000.0; // 常数，每秒钟包含的时钟数
clock_t start_time = clock(); // 开始的时钟数
// 选择矩阵乘法方案
//matrix_multiply_ijk(mat1, mat2, mat3, matrix_n); // 矩阵乘法
matrix_multiply_ikj(mat1, mat2, mat3, matrix_n);
double elapseMills = (clock()-start_time) / clocks_PerMills;
cout << "The routine run time: " << elapseMills << "ms" << endl;
cout << "clock_perMils: " << clocks_PerMills << endl;
//matrix_print(mat3, matrix_n);
// matrix_multiply_ikj(mat1, mat2, mat3, matrix_n);
// matrix_print(mat3, matrix_n);
// 释放内存
for(int i=0; i<numberOfRows; i++)
{
delete mat1[i];
delete mat2[i];
delete mat3[i];
}
delete mat1;
delete mat2;
delete mat3;
return 0;
}
// 计算矩阵乘法 ijk
void matrix_multiply_ijk(int **a, int **b, int **c, int n) // n表示方阵的阶数
{
for(int i=0; i<n; i++)
{
for(int j=0; j<n; j++)
{
int sum = 0;
for(int k=0; k<n; k++)
{
sum += a[i][k]*b[k][j];
}
c[i][j] = sum;
}
}
}
// 计算矩阵乘法 ikj
void matrix_multiply_ikj(int **a, int **b, int **c, int n) // n表示方阵的阶数
{
for(int i=0; i<n; i++)
{
for(int k=0; k<n; k++)
{
int sum = 0;
int j;
for(j=0; j<n; j++)
{
sum += a[i][k]*b[k][j];
}
c[i][j] = sum;
}
}
}
// 输出矩阵
void matrix_print(int **a, int n)
{
for(int i=0; i<n; i++)
{
for(int j=0; j<n; j++)
{
cout << a[i][j] << " ";
}
cout << endl;
}
cout << endl;
}
----------------------------------------------------end--------------------------------------------------------
