C++数据结构与算法 队列的应用之图元识别

图元识别：

数字化图像可以看作m*m的矩阵，单色如图中，像素点的值为0，1.值为0的点表示背景，为1的点表示图元上的一个点。两个相邻的图元像素是同一个图元的像素，图元识别就是给同一个图元的像素做标记。

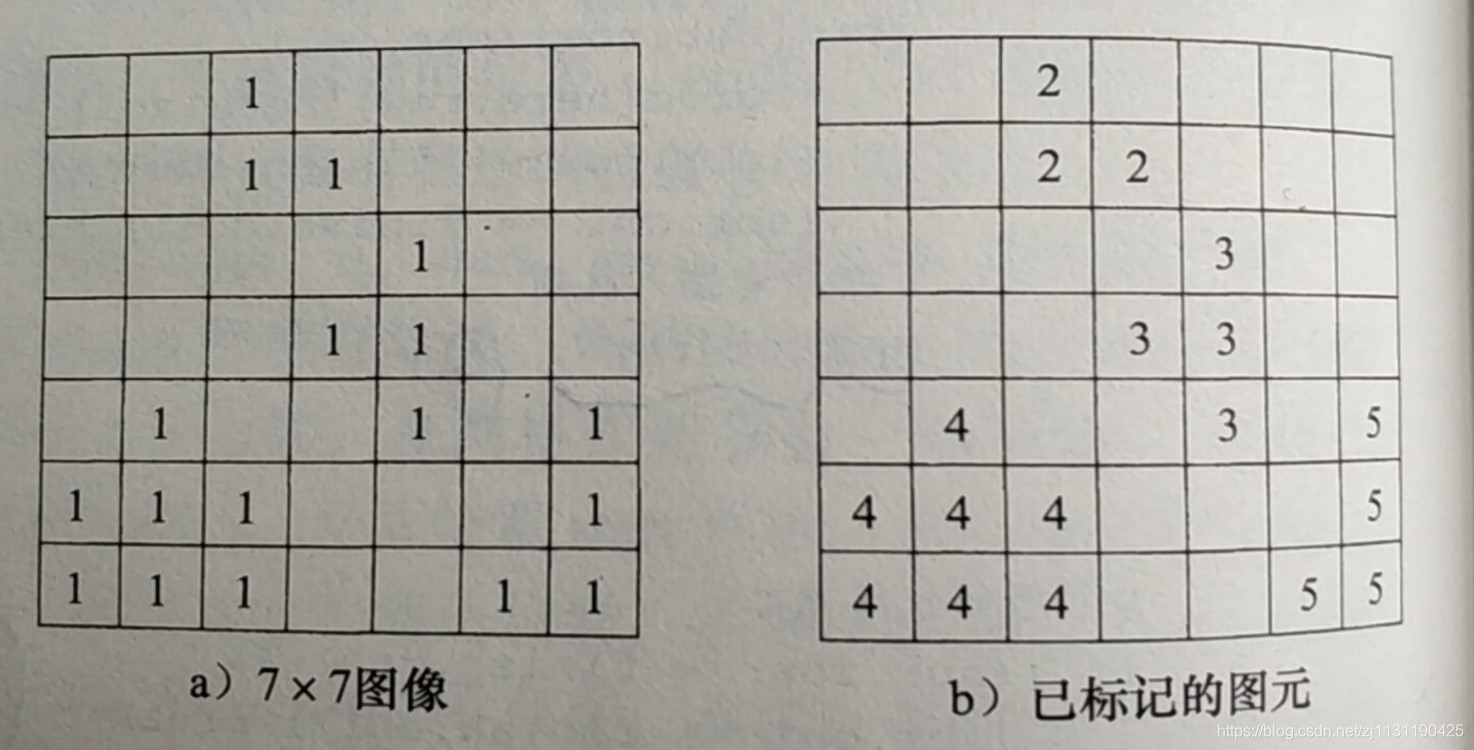
原理如上图所示。

算法思路：

通过扫描像素来识别图元，采用逐行扫描的方式，当扫描到一个未标记图元像素的时候，给他一个图元标记，将其作为一个新图元种子，通过识别标记所有与该种子相邻的元素，来寻找到剩余的像素点。与种子相邻的像素点称为1-间距像素，然后识别和标记与1-间距相邻的所有未标记的像素，这些像素称为2-间距像素。接着标记与2-间距相邻的像素点。直到标记完所有的像素点为止。

算法实现：

#include <iostream>
#include "E:\back_up\code\c_plus_code\dequeue\external_file\queue.h"
using namespace std;
 
// 迷宫
template<typename T>
void print_array(T **a, int size)
{
	for(int i=0; i<size; i++)
	{
		for(int j=0; j<size; j++)
		{
			cout << a[i][j] << " ";
		}
		cout << endl;
	}
	cout << endl;
}
 
 
class position    // 存储位置坐标 
{
	public:
	int row;
	int col;
	position()
	{
		row = 0;
		col = 0;
	}
	
	position(int row, int col)
	{
		this->row = row;
		this->col = col;
	}
	
	/*
	void add_offset(position& ps)
	{
		row += ps.row;
		col += ps.col;
	}
	*/
	 
}; 
 
 
void labelCompents(int** graph, int graphSize)  // 标记图元 
{
	// 参数：原始图像， 图像大小
	// 给图像的边缘添加一层背景（0）
	int** new_graph = new int*[graphSize+2];
	for(int i=0; i<graphSize+2; i++)
	{
		new_graph[i] = new int[graphSize+2];
	} 
	for(int i=0; i<graphSize+2; i++)
	{
		for(int j=0; j<graphSize+2; j++)
		{
			if(i==0 || i==graphSize+2-1)   // 图元添加背景像素 
			{
				new_graph[i][j] = 0;
			}
			else if(j==0 || j==graphSize+2-1)   // 图元添加背景像素 
			{
				new_graph[i][j] = 0;
			}
			else
			{
				new_graph[i][j] = graph[i-1][j-1]; 
			}
		}
	}
	
	cout << "原始图像： " << endl;
	print_array(new_graph, graphSize+2);
	
	// 寻找图元
	// 初始化偏移量
	position offset[4];
	// 向右偏移  index=0 
	offset[0].row = 0;
	offset[0].col = 1; 
	// 向下偏移  index=1
	offset[1].row = 1;
	offset[1].col = 0;
	// 向左偏移   index=2
	offset[2].row = 0;
	offset[2].col = -1;
	// 向上偏移   index=3
	offset[3].row = -1;
	offset[3].col = 0; 	
 
	int direction_number = 4;   // 一个方格相邻位置的个数 
	
	queue<position> q1;
	position current_position;   // 当前的位置
	position neighbor;   // 相邻位置 
	int id = 1;  // 图元的标号
	// 开始扫描图像
	for(int i=0; i<graphSize+2; i++)
	{
		for(int j=0; j<graphSize+2; j++)
		{
			if(new_graph[i][j]==1)
			{
				new_graph[i][j] = ++id;
				// 将这个位置标记为当前位置，也是图元种子 
				current_position.row = i;
				current_position.col = j;
				while(true)
				{
					for(int cnt=0; cnt<direction_number; cnt++)
					{
						// 确定相邻的位置 
						neighbor.row = current_position.row + offset[cnt].row;
						neighbor.col = current_position.col + offset[cnt].col;
						if(new_graph[neighbor.row][neighbor.col]==1)   // 相邻位置满足条件 
						{
							new_graph[neighbor.row][neighbor.col] = id;
							q1.push(neighbor); 
						} 
					}
					if(q1.empty())
					{
						break;     // 当前编号标记完毕，寻找下一个编号 
					}
					current_position = q1.front();   
					q1.pop();
				}		 
			}
		}
	} 
	cout << "标记后的图元： " << endl;
	print_array(new_graph, graphSize+2); 	 	
}
 
 
int main(int argc, char *argv[])
{	
    int map_size = 10;
    int input_map[10][10] = {
   	                   {0,1,1,1,0,0,0,0,0,0},
   	                   {0,1,1,0,0,0,0,0,0,0},
					   {0,0,1,1,0,1,0,0,0,0},
					   {0,1,0,1,0,1,1,1,1,0},
					   {0,1,0,1,0,1,1,0,0,1},
					   {1,1,0,0,0,1,1,1,0,1},
					   {1,1,0,0,0,1,0,0,0,1},
					   {1,0,0,0,0,0,0,1,0,0},
					   {0,0,0,0,1,1,1,1,0,0},
					   {0,0,0,0,0,0,1,0,0,0} 
                      };
    // 数据转换 
	int** map_in = new int*[map_size];
	for(int i=0; i<map_size; i++)
	{
		map_in[i] = new int[map_size];
	}
	for(int i=0; i<map_size; i++)
	{
		for(int j=0; j<map_size; j++)
		{
			map_in[i][j] = input_map[i][j];
		}
	}
	
	// 将原始地图转换为指针的形式
	labelCompents(map_in, map_size);    
	return 0;
}

运行结果：

上述的图元标记算法中应用到了很多迷宫最短路径中的方法：https://blog.csdn.net/zj1131190425/article/details/88086506

----------------------------------------------------------------------------------