C++数据结构与算法 竞赛树, 二叉搜索树
竞赛树：
tournament tree, 也是以可完全二叉树，所以使用数组描述效率最好，竞赛树的基本操作是替换最大(小)元素
赢者树和输者树：
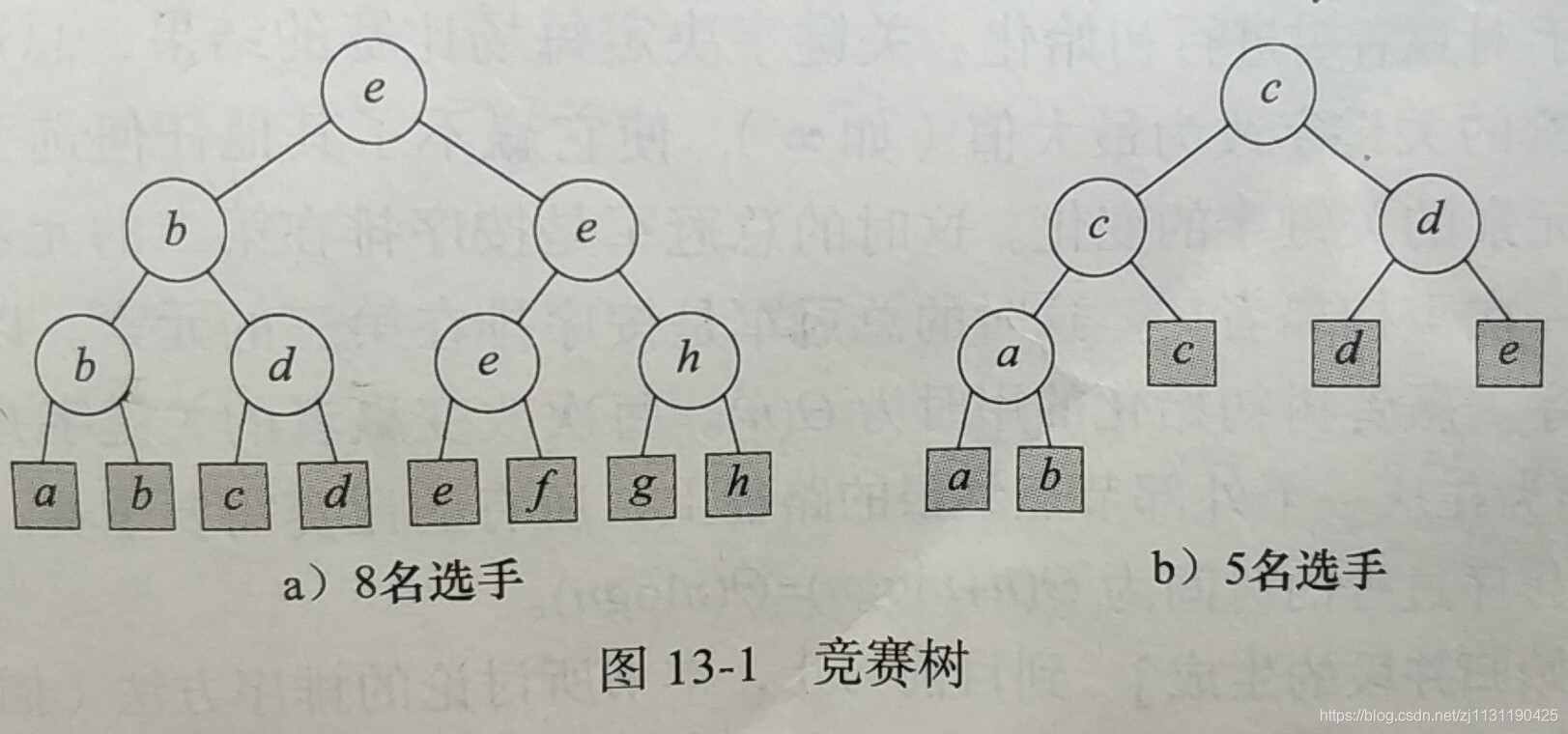
为了便于实现，需要将赢者树限制为完全二叉树。n个参与者的赢者树，具有n个外部节点，n-1个内部节点。每个内部节点记录的是在该节点比赛的赢者。
最大赢者树和最小赢者树：
为了确定输赢者，给每个选手一个分数，分数最大挥着最小的获胜，称为最大最小赢者树：
赢者树的初始化：
采用二叉树的后序遍历方法。每遍历一个节点，就相当于进行一场比赛。
排序：
内部排序法： 例如堆排序，插入排序，需要将排序的元素全部放入计算机内存进行排序，但是当待排序的元素数量超出内存的大小时，就需要使用外部排序。
外部排序步骤：
1. 生成一些初始的归并段（有序的部分待排序元素）
2. 合并这些归并段（利用赢者树）
C++实现赢者树：
假设用完全二叉树的数组表示赢者树，一棵赢者树有n个选手，则需要n-1个内部节点tree[1:n-1]，选手用数组player[1:n]表示。因此tree[i]是数组player的一个索引。
因此，必须确定外外部节点player[i]的父节点tree[P]。
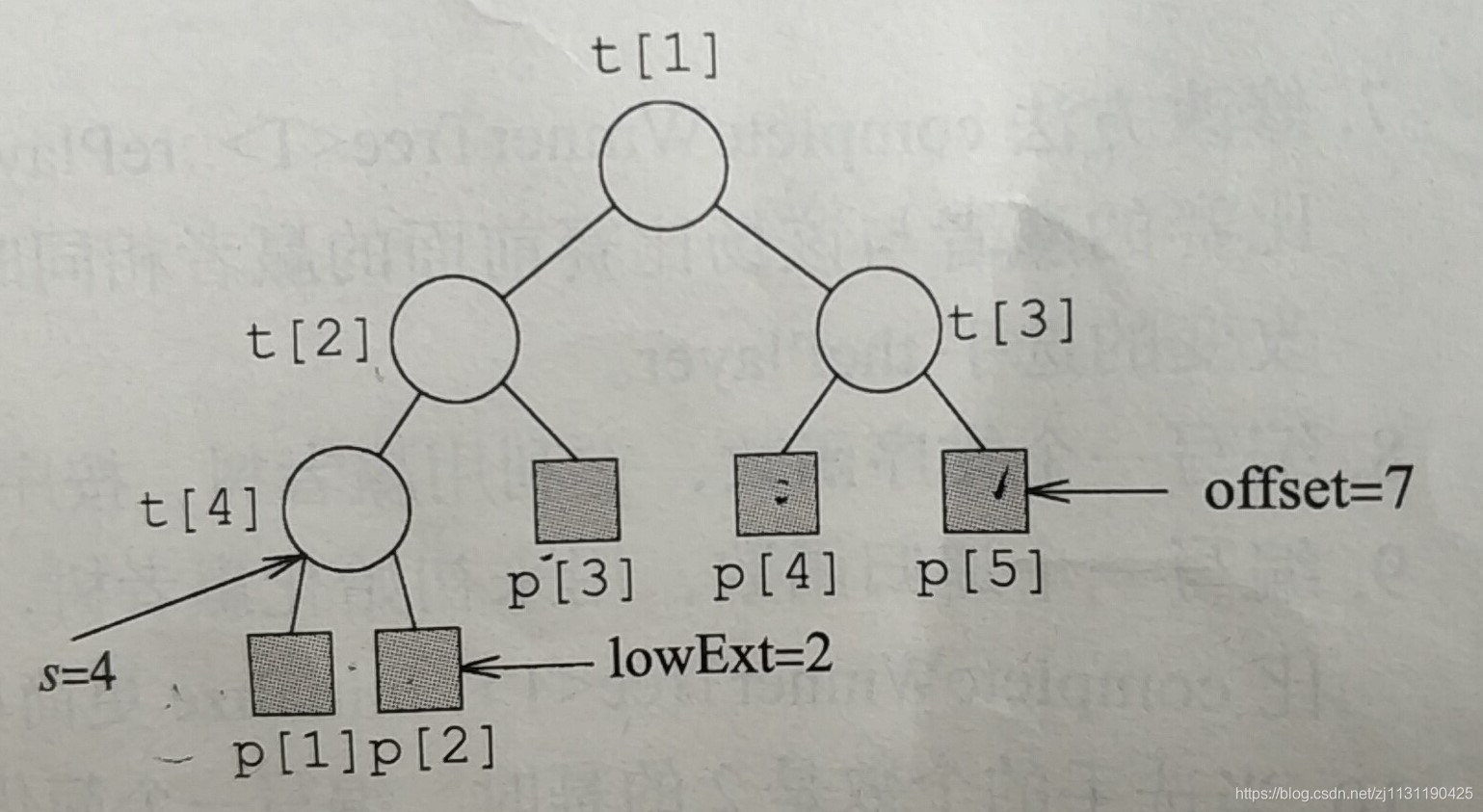
选手个数n,内部节点个数n-1,最底层最左端的内部节点编号为2^s,其中s = 【log2(n-1)】, 最底层内部节点的个数n-s.最底层外部节点的个数lowExt = 2*(n-s),取offset = 2*s-1.则对于任何一个外部节点player[i], 其父节点tree[P]由以下公式给出：
赢者树的初始化：
为了初始化赢者树，需要从右孩子选手开始，进行他们所参加的比赛，而且逐层往上，只要是右孩子上升到比赛节点，就可以进行比赛。如在上图中，先进性p[2]的比赛，在进行p[3]的比赛得到结果t[2]，但是t[2]的比赛不能进行，因为它是左孩子，所以需要进行p[5]的比赛，得到t[3]，t[3]是右孩子，进行t[3]的比赛，得到t[1];
重新组织比赛：
当选手theplayer的值发生变化时，从外部节点player[theplayer]到根tree[1]的路径上，一部分或全部比赛都要重赛。
竞赛树的实现代码：
#ifndef TOURNAMENT_TREE_H
#define TOURNAMENT_TREE_H
#include <iostream>
#include <cmath>
using namespace std;
template<class T>
class completeWinnerTree
{
public:
completeWinnerTree(T *thePlayer, int theNumberOfPlayers)
{
tree = NULL;
initialize(thePlayer, theNumberOfPlayers);
}
~completeWinnerTree() {delete [] tree;}
void initialize(T*, int);
int winner() const//返回赢者树的根节点。
{
return tree[1];
}
int winner(int i) const//返回第i个节点的胜者
{
return (i < numberOfPlayers) ? tree[i] : 0;
}
// return winner of match at node i
void rePlay(int);
void output() const;
private:
int lowExt; // lowest-level external nodes
int offset; // 2^log(n-1) - 1
int *tree; // array for winner tree
int numberOfPlayers;
T *player; // array of players
void play(int, int, int);
};
template<class T>
void completeWinnerTree<T>::play(int p, int leftChild, int rightChild)
{
// play matches beginning at tree[p]
// leftChild is left child of p
// rightChild is right child of p
//如果左节点的数据较小则左节点晋级。
tree[p] = (player[leftChild] <= player[rightChild]) ?
leftChild : rightChild;
// more matches possible if at right child
while (p % 2 == 1 && p > 1)//如果当前节点是右节点，且不是根节点，那么继续进行比赛。
{// at a right child
tree[p / 2] = (player[tree[p - 1]] <= player[tree[p]]) ?tree[p - 1] : tree[p];
p /= 2; // go to parent
}
}
template<class T>
void completeWinnerTree<T>::initialize(T *thePlayer, int theNumberOfPlayers)
{
// Create winner tree for thePlayer[1:numberOfPlayers].
//比赛参与者最少2个人否则报错
int n = theNumberOfPlayers;
if (n < 2)
{
//throw illegalParameterValue("must have at least 2 players");
cout << "The players must > 2" << endl;
exit(0);
}
player = thePlayer;//获取外节点数组。
numberOfPlayers = n;
delete [] tree;//初始化树节点，因为第0位置不放数据，所以实际大小为n-1.
tree = new int [n];//
// compute s = 2^log (n-1)
int i, s;//计算内部节点最左边的节点编号，下面采取寻访方式计算s，非常巧妙
for (s = 1; 2 * s <= n - 1; s += s);
lowExt = 2 * (n - s);//计算最低层外部节点的个数
offset = 2 * s - 1;
// play matches for lowest-level external nodes
for (i = 2; i <= lowExt; i += 2)//首先进行最底层外部节点的比赛，i从2开始且每次+2是为了每次都是从右子节点开始进行比赛
play((offset + i) / 2, i - 1, i);
// handle remaining external nodes
if (n % 2 == 1)//如果倒数第二层最左边的元素为某个父节点的右节点，则进行如下处理，即比赛。
{// special case for odd n, play internal and exteral node
play(n/2, tree[n - 1], lowExt + 1);
i = lowExt + 3;//然后从lowExt+3即倒数第二层外部节点的右儿子开始比赛
}
else i = lowExt + 2;//否则右儿子为lowExt+2
// i is left-most remaining external node
for (; i <= n; i += 2)//然后开始处理倒数第二层其他外部节点。
play((i - lowExt + n - 1) / 2, i - 1, i);//play每次都会处理到上层的左节点为止，然后再去处理下一个右节点。
}
template<class T>
void completeWinnerTree<T>::rePlay(int thePlayer)
{// Replay matches for player thePlayer.
int n = numberOfPlayers;
if (thePlayer <= 0 || thePlayer > n)//改变的选手必须要在范围内。
{
cout << "Invalid index" << endl;
exit(0);
}
//throw illegalParameterValue("Player index is illegal");
int matchNode, // node where next match is to be played需要重赛的父节点
leftChild, // left child of matchNode该父节点的左孩子
rightChild; // right child of matchNode右孩子
// find first match node and its children
if (thePlayer <= lowExt)//如果改变的参数在最低层
{
// begin at lowest level
matchNode = (offset + thePlayer) / 2;//要求重赛的父节点
leftChild = 2 * matchNode - offset;//及其子节点
rightChild = leftChild + 1;
}
else
{
matchNode = (thePlayer - lowExt + n - 1) / 2;//如果要求重赛的选手在倒数第二层的外部节点。
if (2 * matchNode == n - 1)//如果要求重赛的选手在倒数第二层与倒数第一层的交界点处
{
leftChild = tree[2 * matchNode];
rightChild = thePlayer;
}
else//否则在倒数第二层的外部节点处。
{
leftChild = 2 * matchNode - n + 1 + lowExt;
rightChild = leftChild + 1;
}
}
tree[matchNode] = (player[leftChild] <= player[rightChild])//重赛
? leftChild : rightChild;
// special case for second match
if (matchNode == n - 1 && n % 2 == 1)//这里没弄明白。。。
{
matchNode /= 2; // move to parent
tree[matchNode] = (player[tree[n - 1]] <=
player[lowExt + 1]) ?
tree[n - 1] : lowExt + 1;
}
// play remaining matches
matchNode /= 2; // move to parent
for (; matchNode >= 1; matchNode /= 2)//依次往上进行重赛直到主节点。
tree[matchNode] = (player[tree[2 * matchNode]] <=player[tree[2 * matchNode + 1]])?tree[2 * matchNode] : tree[2 * matchNode + 1];
}
template<typename T>
void completeWinnerTree<T>::output() const
{
cout << "number of players: " << numberOfPlayers << endl;
cout << "lowExt = " << lowExt << endl;
cout << "offset = " << offset << endl;
for(int i=1; i<numberOfPlayers; i++)
{
cout << tree[i] << " ";
}
cout << endl;
}
#endif
代码来源：https://www.cise.ufl.edu/~sahni/dsaac
搜索树
搜索树适用于字典描述，与跳表和散列相比，二叉搜索树和平衡搜索树使用更加灵活，在最坏的情况下性能有保证。
二叉搜索树：
是一棵二叉树，可能为空，非空的二叉搜索树满足以下特征：
1.每个元素都有唯一的关键字
2.根节点的左子树中，元素的关键字都小于根节点的关键字
3.根节点的右子树中，元素的关键字都大于根节点的关键字
4.根节点左右子树也都是二叉搜索树
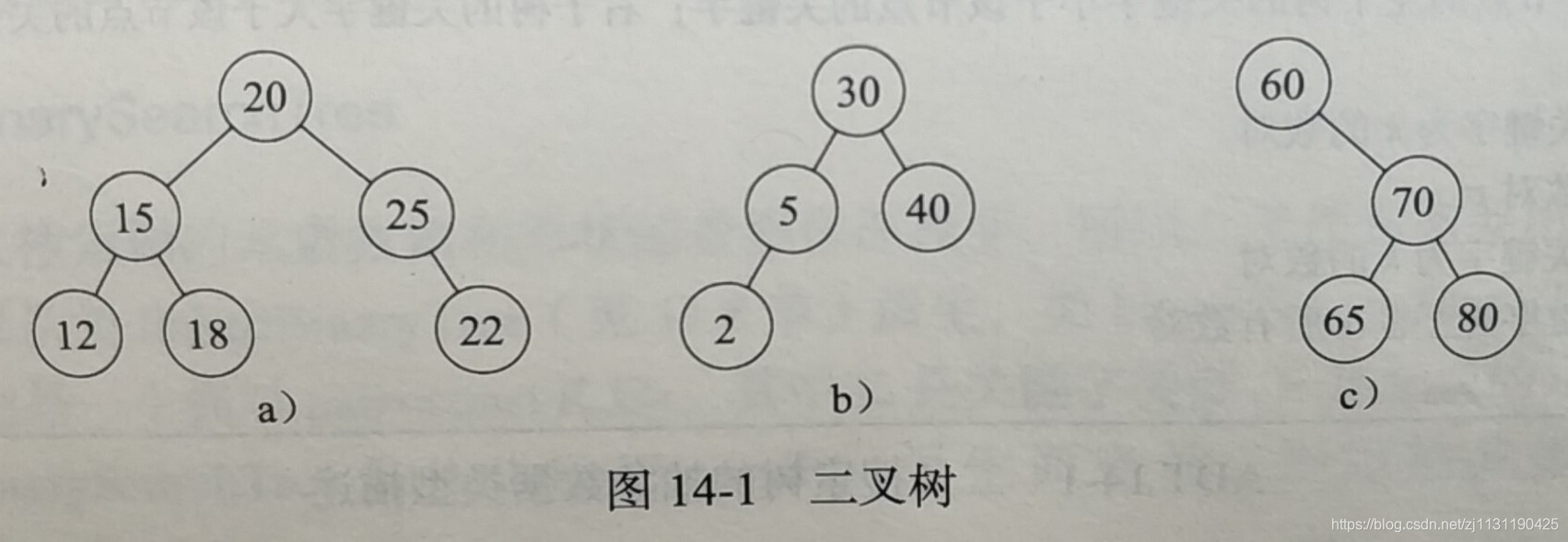
a就不是二叉搜索树（不满足4），bc是二叉搜索树。
注： 有重复值的二叉搜索树， 小于-->小于等于
索引二叉搜索树：
源于普通的二叉搜索树，只是在每个节点中添加一个leftSize域，表示该节点的左子树的元素个数：
二叉搜索树的操作：
1. 搜索：
假设需要查找的关键字为theKey,则先从根节点开始查找，如果为空，则树不包含任何元素；否则，将theKey和根节点的关键字进行比较，如果等于，则查找成功，如果theKey小于根节点的关键字，则查找左子树即可，否则，查找右子树。
2. 插入
假设要在二叉搜索树中插入一个元素，首先通过查找来确定，要插入的元素的关键字在树中是否存在，如果存在，则用插入元素的value覆盖掉原来的value，否则，将元素插入树中：
3. 删除
要考虑三种情况：
1.要删除的节点是树叶：
2.要删除的节点有一棵子树
3.要删除的节点有两棵子树
二叉搜索树的实现;
// 定义二叉搜索树树
#ifndef BSTREE_H
#define BSTREE_H
#include <algorithm>
#include <iostream>
using namespace std;
// 定义二叉搜索树的节点
template<typename K=int, typename V=int> // key: value类型的节点
struct BSTreeNode
{
BSTreeNode* leftchild;
BSTreeNode* rightchild;
K key;
V value;
BSTreeNode(K& theKey, V& theValue)
{
key = theKey;
value = theValue;
leftchild = NULL;
rightchild = NULL;
}
};
template<typename K, typename V>
class BSTree
{
typedef BSTreeNode<K, V> BSTreeNode;
private:
BSTreeNode* root; // 二叉搜索树的根节点
int treeSize;
void destory(BSTreeNode* mroot); // 删除二叉树的所有节点 // 析构函数
BSTreeNode* find(K theKey, BSTreeNode* mroot);
void insert(K theKey, V theValue, BSTreeNode* mroot);
void remove(K theKey, BSTreeNode* mroot); // 删除特定的节点
void out_put(BSTree* mroot);
public:
BSTree();
~BSTree();
// void destory();
// 查找二叉树的节点
BSTreeNode* find(K theKey); // 参数：键值
void insert(K theKey, V theValue);
void remove(K theKey);
void out_put();
};
template<typename K, typename V>
void BSTree<K, V>::destory(BSTreeNode* mroot)
{
// 删除所有节点 递归调用
if(mroot!=NULL)
{
destory(mroot->leftchild);
destory(mroot->rightchild);
delete mroot;
}
}
template<typename K, typename V>
BSTree<K, V>::BSTree()
{
treeSize = 0;
root = NULL;
}
template<typename K, typename V>
BSTree<K, V>::~BSTree()
{
// 删除二叉树的节点
destory(root);
}
template<typename K, typename V>
BSTreeNode* BSTree<K, V>::find(K theKey)
{
// 二叉搜索树的查找函数
// 根据关键字查找：
return find(theKey, root);
}
template<typename K, typename V>
BSTreeNode* BSTree<K, V>::find(K theKey, BSTreeNode* mroot)
{
if(mroot != NULL)
{
if(mroot->key==theKey)
{
return mroot;
}
else if(mroot->key>theKey) // 搜索左子树
{
return find(theKey, mroot->leftchild); // 递归的方法
}
else // 搜索右子树
{
return find(theKey, mroot->rightchild);
}
}
return NULL; // 没有找到
}
template<typename K, typename V>
void BSTree<K, V>::insert(K theKey, V theValue, BSTreeNode* mroot)
{
// NULL
if(mroot==NULL)
{
mroot = new BSTreeNode(theKey, theValue);
return; // 递归结束
}
if(mroot->key==theKey) // 关键字已经存在
{
mroot->value = theValue;
return; // 结束递归
}
else if(theKey < mroot->key) // 插入左子树
{
insert(theKey, theValue, mroot->leftchild);
}
else // 插入右子树
{
insert(theKey, theValue, mroot->rightchild);
}
}
template<typename K, typename V>
void BSTree<K, V>::insert(K theKey, V theValue)
{
insert(theKey, theValue, root);
}
template<typename K, typename V>
void BSTree<K, V>::remove(K theKey, BSTreeNode* mroot)
{
/*
if(mroot==NULL) // 结束的条件
{
cout << "No such node" << endl;
return;
}
*/
// 只有一个节点
if(mroot->leftchild==NULL && mroot->rightchild==NULL) // 最底层的节点
{
if(root->key==theKey) // 是要查找的节点
{
delete mroot;
mroot = NULL;
return;
}
}
if(theKey<mroot->key) // 搜索左子树
{
remove(theKey, mroot->leftchild);
}
else if(theKey>mroot->key)
{
remove(theKey, mroot->rightchild); // 搜索右子树
}
else // 相等。且不是最底层的节点
{
BSTreeNode* del = NULL; // 临时的指针
if(mroot->leftchild==NULL) // 只有右孩子
{
del = mroot;
mroot = mroot->rightchild; // 取右孩子
delete del;
del = NULL;
return;
}
else if(mroot->rightchild==NULL) // 只有左孩子
{
del = mroot;
mroot = mroot->leftchild;
delete del;
del = NULL;
return;
}
else // 要删除的节点有左右子树
{
BSTreeNode* rightFirst = mroot->rightchild; // 获取要删除的节点的右孩子
while(rightFirst->leftchild!=NULL)
{
rightFirst = rightFirst->leftchild;
}
// 交换
// 将要删除的节点交换到最底层
swap(mroot->key, rightFirst->key);
swap(mroot->value, rightFirst->value);
remove(theKey, mroot->rightchild); // 接着删除
return; // ?
}
}
}
template<typename K, typename V>
void BSTree<K, V>::remove(K theKey)
{
remove(theKey, root);
}
template<typename K, typename V>
void BSTree<K, V>::out_put(BSTreeNode* mroot)
{
if(mroot==NULL)
{
return;
}
out_put(mroot->leftchild);
cout << "key: " << mroot->key << " value: " << mroot->value << " ";
out_put(mroot->rightchild);
}
template<typename K, typename V>
void BSTree<K, V>::out_put()
{
out_put(root);
}
#endif
