求凸包及凸包上距离最远点对

证明axb的模是a，b为邻边的平行四边形面积：http://www.docin.com/p-634375594.html

在一个二维平面上距离最远的两个点一定在凸包上。

求凸包这里给出

Graham扫描法

时间复杂度：O(n㏒n)
思路：Graham扫描的思想和Jarris步进法类似，也是先找到凸包上的一个点，然后从那个点开始按逆时针方向逐个找凸包上的点，但它不是利用夹角。

步骤：

1. 把所有点放在二维坐标系中，则纵坐标最小的点一定是凸包上的点，如图中的P0。
2. 把所有点的坐标平移一下，使 P0 作为原点，如上图。
3. 计算各个点相对于 P0 的幅角 α ，按从小到大的顺序对各个点排序。当 α 相同时，距离 P0 比较近的排在前面。例如上图得到的结果为 P1，P2，P3，P4，P5，P6，P7，P8。我们由几何知识可以知道，结果中第一个点 P1 和最后一个点 P8 一定是凸包上的点。
   （以上是准备步骤，以下开始求凸包）
   以上，我们已经知道了凸包上的第一个点 P0 和第二个点 P1，我们把它们放在栈里面。现在从步骤3求得的那个结果里，把 P1 后面的那个点拿出来做当前点，即 P2 。接下来开始找第三个点：
4. 连接P0和栈顶的那个点，得到直线 L 。看当前点是在直线 L 的右边还是左边。如果在直线的右边就执行步骤5；如果在直线上，或者在直线的左边就执行步骤6。
5. 如果在右边，则栈顶的那个元素不是凸包上的点，把栈顶元素出栈。执行步骤4。
6. 当前点是凸包上的点，把它压入栈，执行步骤7。
7. 检查当前的点 P2 是不是步骤3那个结果的最后一个元素。是最后一个元素的话就结束。如果不是的话就把 P2 后面那个点做当前点，返回步骤4。

最后，栈中的元素就是凸包上的点了。
以下为用Graham扫描法动态求解的过程：

bool cmp(node a,node b)
{
    double A=atan2(a.y-p0.y,a.x-p0.x);
    double B=atan2(b.y-p0.y,b.x-p0.x);
    return A==B?a.x<b.x:A<B;
}
long long xmul(int x,int y,int xx,int yy)
{
    return 1ll*x*yy-1ll*xx*y;
}
long long compare(node a,node b,node c)
{
    return xmul(b.x-c.x,b.y-c.y,c.x-a.x,c.y-a.y);
}
void find()
{
    p0=(node){inf,inf};
    int k=0;
    for(int i=1;i<=n;++i)
        if(p0.y>p[i].y||(p0.y==p[i].y&&p0.x>p[i].x))
        p0=p[i],k=i;
    swap(p[k],p[1]);
    sort(p+1,p+1+n,cmp);
    s[1]=p[1];s[2]=p[2];top=2;
    for(int i=3;i<=n;)
    {
        if(top>=2&&compare(s[top-1],p[i],s[top])>=0)top--;
        else s[++top]=p[i++];
    }
}

然后如何求距离最大点对呢，我们运用旋转卡（qia）壳

证明及性质：https://www.cnblogs.com/Booble/archive/2011/04/03/2004865.html

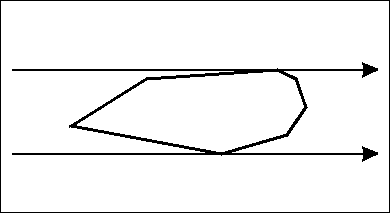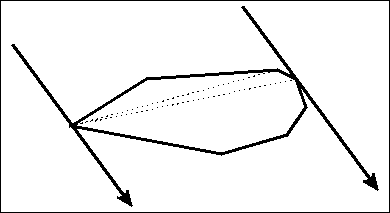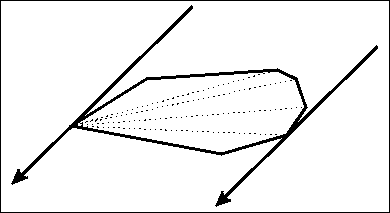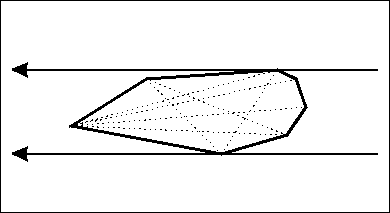
long long dis(node a,node b)
{
    return 1ll*(a.x-b.x)*(a.x-b.x)+1ll*(a.y-b.y)*(a.y-b.y);
}
long long getmax()
{
    long long re=0;
    if(top==2)return dis(s[1],s[2]);
    s[++top]=s[1];
    int j=3;
    for(int i=1;i<=top;++i)
    {
        while(compare(s[i],s[i+1],s[j])<compare(s[i],s[i+1],s[j+1]))
        {
            j=(j+1)%top;
        }
        re=max(re,max(dis(s[i],s[j]),dis(s[i+1],s[j])));
    }
    return re;
}