Good Bye 2019(前五题题解)
Good Bye 2019(前五题题解)
这套也是后来补得。
我太菜了,第三题就卡着了。想了好久才做出来,要是参加了绝对掉分。
D题是人生中做完的第一道交互题,不容易。
A.Card Game
题目大意:一共有n张互不相同的牌,玩家1有k1张牌,玩家2有k2张牌。两个人每次都会拿出一张牌,牌号大的人会得到这张牌,直到一方没牌。问第一个人能否会获胜。
这就是我们从小玩的比大小游戏。
在广大劳动人民的实践后得出来结论是有最大的牌的人获胜。
代码如下:

1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cstring> 5 #include <vector> 6 #define rep(x, l, r) for(int x = l; x <= r; x++) 7 #define repd(x, r, l) for(int x = r; x >= l; x--) 8 #define clr(x, y) memset(x, y, sizeof(x)) 9 #define all(x) x.begin(), x.end() 10 #define pb push_back 11 #define mp make_pair 12 #define MAXN 13 #define fi first 14 #define se second 15 #define SZ(x) ((int)x.size()) 16 using namespace std; 17 typedef long long ll; 18 typedef vector<int> vi; 19 typedef pair<int, int> pii; 20 const int INF = 1 << 30; 21 const int p = 1000000009; 22 int lowbit(int x){ return x & (-x);} 23 int fast_power(int a, int b){ int x; for(x = 1; b; b >>= 1){ if(b & 1) x = 1ll * x * a % p; a = 1ll * a * a % p;} return x % p;} 24 25 int main(){ 26 int t; 27 scanf("%d", &t); 28 rep(times, 1, t){ 29 int n, k1, k2; 30 scanf("%d%d%d", &n, &k1, &k2); 31 int maxx1 = 0, maxx2 = 0; 32 rep(i, 1, k1){ 33 int x; 34 scanf("%d", &x); 35 maxx1 = max(maxx1, x); 36 } 37 rep(i, 1, k2){ 38 int x; 39 scanf("%d", &x); 40 maxx2 = max(maxx2, x); 41 } 42 if(maxx1 > maxx2) puts("YES"); 43 else puts("NO"); 44 } 45 return 0; 46 }
B.Interesting Subarray
题目大意:有一个数列a,让你找任意一个子段满足子段的最大值减最小值大于等于子段长度。
感觉这套的B题也比之前的难了点,看着屏幕愣了半天,可能最近脑子不对劲。
如果子段(l,r)满足条件,那么必定存在i,j满足a[i] - i < a[j] - j ,或者a[i] + i > a[j] + j。
那么只需记录下在所有的i,j( i <= j ),最小的a[i] - i和最大的a[i] + i,如果满足上面的条件就输出这一对。
代码如下:

1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cstring> 5 #include <vector> 6 #define rep(x, l, r) for(int x = l; x <= r; x++) 7 #define repd(x, r, l) for(int x = r; x >= l; x--) 8 #define clr(x, y) memset(x, y, sizeof(x)) 9 #define all(x) x.begin(), x.end() 10 #define pb push_back 11 #define mp make_pair 12 #define MAXN 200005 13 #define fi first 14 #define se second 15 #define SZ(x) ((int)x.size()) 16 using namespace std; 17 typedef long long ll; 18 typedef vector<int> vi; 19 typedef pair<int, int> pii; 20 const int INF = 1 << 30; 21 const int p = 1000000009; 22 int lowbit(int x){ return x & (-x);} 23 int fast_power(int a, int b){ int x; for(x = 1; b; b >>= 1){ if(b & 1) x = 1ll * x * a % p; a = 1ll * a * a % p;} return x % p;} 24 25 int a[MAXN]; 26 27 int main(){ 28 int t; 29 scanf("%d", &t); 30 rep(times, 1, t){ 31 int n; 32 scanf("%d", &n); 33 rep(i, 1, n) scanf("%d", &a[i]); 34 int s = INF, id = 0, ans = 0; 35 rep(i, 1, n){ 36 if(s < a[i] - i){ 37 printf("YES\n%d %d\n", id, i); 38 ans = 1; 39 break; 40 } 41 if(a[i] - i < s){ 42 s = a[i] - i; 43 id = i; 44 } 45 } 46 if(!ans){ 47 s = 0, id = 0; 48 rep(i, 1, n){ 49 if(s > a[i] + i){ 50 printf("YES\n%d %d\n", id, i); 51 ans = 1; 52 break; 53 } 54 if(a[i] + i > s){ 55 s = a[i] + i; 56 id = i; 57 } 58 } 59 } 60 if(!ans) puts("NO"); 61 } 62 return 0; 63 }
C.Make Good
题目大意:给你一串数字,让你在其中插入最多3个数字,使得这些数字的总和等于异或的2倍,只要给出任何一种方案即可。
首先这串数字是和我们没关系了,我们需要的只是它们的异或以及和。
很显然,必定存在一种方案只放一个数字就能成立(不要问我为什么,程序员不需要证明)。
然后么将异或的乘个二,按照二进制来计算。
对于每一位,要是该位的为1,会对和产生1的贡献,对异或产生2的贡献,那么对于一个二进制位,要是这两个数不同,插入的数该位一定为1。
感觉解释的有点模糊……那就来个样例解释一下。
以下以[1,2,3,7]为例:
和:13 二进制:01101
异或:7 二进制:00111
异或的先乘个2也就是右移一位,为01110
0110 | 1
0111 | 0
两位置不同,答案该位为1,即加上1 << 0,变成1
和变成01110,异或变成01100,最后一位已经相同了,舍掉
011 | 1
011 | 0
不同,答案变成3,两数分别变成1000和0100,同样舍最后一位
10 | 0
01 | 0 相同
1 | 0
0 | 1 不同,答案变成11
| 1
| 1 相同
插入后数列为 1, 2, 3, 7 , 11符合条件
具体代码实现:

1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cstring> 5 #include <vector> 6 #define rep(x, l, r) for(int x = l; x <= r; x++) 7 #define repd(x, r, l) for(int x = r; x >= l; x--) 8 #define clr(x, y) memset(x, y, sizeof(x)) 9 #define all(x) x.begin(), x.end() 10 #define pb push_back 11 #define mp make_pair 12 #define MAXN 13 #define fi first 14 #define se second 15 #define SZ(x) ((int)x.size()) 16 using namespace std; 17 typedef long long ll; 18 typedef vector<int> vi; 19 typedef pair<int, int> pii; 20 const int INF = 1 << 30; 21 const int p = 1000000009; 22 int lowbit(int x){ return x & (-x);} 23 int fast_power(int a, int b){ int x; for(x = 1; b; b >>= 1){ if(b & 1) x = 1ll * x * a % p; a = 1ll * a * a % p;} return x % p;} 24 25 int main(){ 26 int t; 27 scanf("%d", &t); 28 rep(times, 1, t){ 29 int n; 30 scanf("%d", &n); 31 ll s1 = 0, s2 = 0; 32 rep(i, 1, n){ 33 ll x; 34 scanf("%lld", &x); 35 s1 += x; 36 s2 ^= x; 37 } 38 s2 <<= 1; 39 ll ans = 0; 40 for(int i = 0; s1 != s2; i++){ 41 if((s1 & 1) ^ (s2 & 1)){ 42 s1 += 1; 43 s2 ^= 2; 44 ans += 1ll << i; 45 } 46 s1 >>= 1; 47 s2 >>= 1; 48 } 49 printf("1\n%lld\n", ans); 50 } 51 return 0; 52 }
D.Strange Device
题目大意:有一个长为n数列a,值已确定,但是你不知道。现在有个设备,你可以输入长为k的上升序列p1,p2,…,pk,进行询问,它会回答ap1,ap2,...,apk中第m小的数在原数列的坐标和这个数的值。现在给你n和k,让你在最多询问n次后回答m的大小。
作为以往交互题直接跳的人,这题拿到一脸懵,后来还是看题解才有的思路。
我们只需要询问k+1次,第i次询问序列为{ x | 1 <= x <= k + 1, x <> i }
假设n = 4, k = 3,询问分别为
2 3 4
1 3 4
1 2 4
1 2 3
这样问有一个好处,第i次询问,若是i <= m,那么返回的必然是[a1..ak +1]中第m + 1小的数,否则返回的数必然是第m小的数。
那么在k+1次询问后,m+1小的数恰好返回了m次,于是我们答案就是返回的较大的一个数的次数。
代码如下:

1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cstring> 5 #include <vector> 6 #include <map> 7 #define rep(x, l, r) for(int x = l; x <= r; x++) 8 #define repd(x, r, l) for(int x = r; x >= l; x--) 9 #define clr(x, y) memset(x, y, sizeof(x)) 10 #define all(x) x.begin(), x.end() 11 #define pb push_back 12 #define mp make_pair 13 #define MAXN 14 #define fi first 15 #define se second 16 #define SZ(x) ((int)x.size()) 17 using namespace std; 18 typedef long long ll; 19 typedef vector<int> vi; 20 typedef pair<int, int> pii; 21 const int INF = 1 << 30; 22 const int p = 1000000009; 23 int lowbit(int x){ return x & (-x);} 24 int fast_power(int a, int b){ int x; for(x = 1; b; b >>= 1){ if(b & 1) x = 1ll * x * a % p; a = 1ll * a * a % p;} return x % p;} 25 26 map<int, int> f; 27 28 int main(){ 29 int n, k; 30 scanf("%d%d", &n, &k); 31 int maxx = 0; 32 rep(i, 1, k + 1){ 33 putchar('?'); 34 rep(j, 1, k + 1){ 35 if(i == j) continue; 36 printf(" %d", j); 37 } 38 puts(""); 39 fflush(stdout); 40 int x, y; 41 scanf("%d%d", &x, &y); 42 f[y]++; 43 maxx = max(maxx, y); 44 } 45 printf("! %d\n", f[maxx]); 46 return 0; 47 }
E.Divide Points
题目大意:给你n个点和它们的坐标,现在给它们两两连上边,如果在同一组为黄色,不同组为蓝色。现在让你给出任意一种分组方案,使得所有长度相同的边颜色相同。
相信大家看到这题目想的都是二分图啊,并查集啊……但我不一样,我想的是:这题目能做嘛……
大佬的做法真是高超,先放上题解里截来的图。

主要思路就是奇偶分类。
我们将点按照横纵坐标的奇偶性,分成4个集合。
其中点上的0,1表示坐标的奇偶性,边上的0,1表示长度平方的奇偶性。
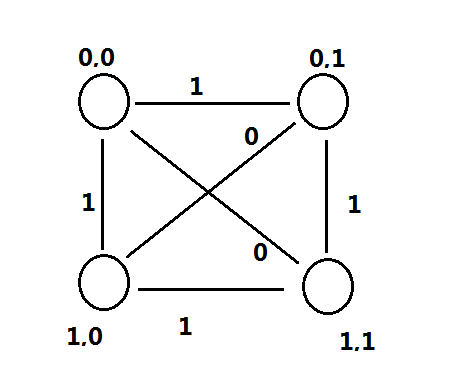
不难得出以上不同集合的点的关系,另外同一集合中的边当然也为0。
那么我们只要将(0,0)和(1,1)放入一组,(0,1)和(1,0)放入另一组,那么偶边(即长度平方为偶数的边)必定是同一组的两点,奇边必定是不同组的两点。当然这有个前提,就是每组都不能为空。
那若是有一组为空呢,图片就变成了这个样子

两个集合连起来也是偶边,自己集合连自己集合也是偶边,似乎无法连接了。
但是我们发现自己连自己横坐标差和纵坐标差都为偶数,和别的集合连得差都为偶数。
我们设同一集合的横坐标差为2k1,纵坐标差为2k2,不同集合的横坐标差为2k1+1,纵坐标差是2k2+1
根据距离公式d = √((x1 - x2) × (x1 + x2) + (y1 - y2) × (y1 - y2))进行计算(方便起见,直接算边长度的平方)。
同一集合相连 = (2k1)2 + (2k2)2 = 4(k12 + k22)
不同集合相连 = (2k1 + 1)2 + (2k2 + 1)2 = 4(k12 + k22 + k1 + k2) + 2
很显然这两个是不会相等的。
那么如果不符合上一个情况,那么按x的奇偶性分组。
可是万一数据只有一个集合呢?
没事把数据缩小一倍就好了,到时候一定会有答案因为点坐标两两不同。
这样为什么可行呢?
因为同一个集合中的点的奇偶性都是相同的,那么我们将它们的最后一位舍弃也是符合原来的大小情况。
代码如下:

1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cstring> 5 #include <vector> 6 #define rep(x, l, r) for(int x = l; x <= r; x++) 7 #define repd(x, r, l) for(int x = r; x >= l; x--) 8 #define clr(x, y) memset(x, y, sizeof(x)) 9 #define all(x) x.begin(), x.end() 10 #define pb push_back 11 #define mp make_pair 12 #define MAXN 1005 13 #define fi first 14 #define se second 15 #define SZ(x) ((int)x.size()) 16 using namespace std; 17 typedef long long ll; 18 typedef vector<int> vi; 19 typedef pair<int, int> pii; 20 const int INF = 1 << 30; 21 const int p = 1000000009; 22 int lowbit(int x){ return x & (-x);} 23 int fast_power(int a, int b){ int x; for(x = 1; b; b >>= 1){ if(b & 1) x = 1ll * x * a % p; a = 1ll * a * a % p;} return x % p;} 24 25 vi ans; 26 int x[MAXN], y[MAXN], cnt[2][2]; 27 28 int main(){ 29 int n; 30 scanf("%d", &n); 31 rep(i, 1, n) scanf("%d%d", &x[i], &y[i]); 32 while(1){ 33 clr(cnt, 0); 34 rep(i, 1, n) cnt[x[i] & 1][y[i] & 1]++; 35 if(cnt[0][1] + cnt[1][0] > 0 && cnt[0][0] + cnt[1][1] > 0){ 36 rep(i, 1, n) 37 if((x[i] & 1) ^ (y[i] & 1)) ans.pb(i); 38 printf("%d\n", SZ(ans)); 39 rep(i, 0, SZ(ans) - 1) printf("%d ", ans[i]); 40 puts(""); 41 return 0; 42 } 43 if(cnt[0][0] + cnt[0][1] > 0 && cnt[1][0] + cnt[1][1] > 0){ 44 rep(i, 1, n) 45 if(x[i] & 1) ans.pb(i); 46 printf("%d\n", SZ(ans)); 47 rep(i, 0, SZ(ans) - 1) printf("%d ", ans[i]); 48 puts(""); 49 return 0; 50 } 51 rep(i, 1, n){ 52 x[i] >>= 1; 53 y[i] >>= 1; 54 } 55 } 56 return 0; 57 }


