相机标定、校正和投影

一相机的成像模型

空间中物体表面的三维坐标点与图像的像素坐标点存在某种关系，需要通过建立相机成像的几何模型来求解。其中，空间中三维坐标点存在于世界坐标系、相机坐标系，二维坐标点存在于图像坐标系、像素坐标系；世界坐标系到相机坐标系的变换关系就是相机的外参标定【姿态R和位置t】，相机坐标系到像素坐标系关系就是相机的内参标定【焦距f、主点坐标（u0、v0）、像素尺寸(dx, dy)】。

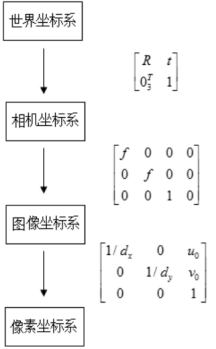
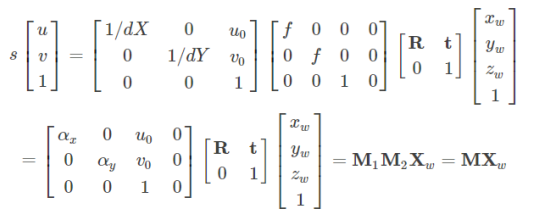
其中：M1-内参矩阵、M2-外参矩阵

1 为什么要有相机的内参标定？

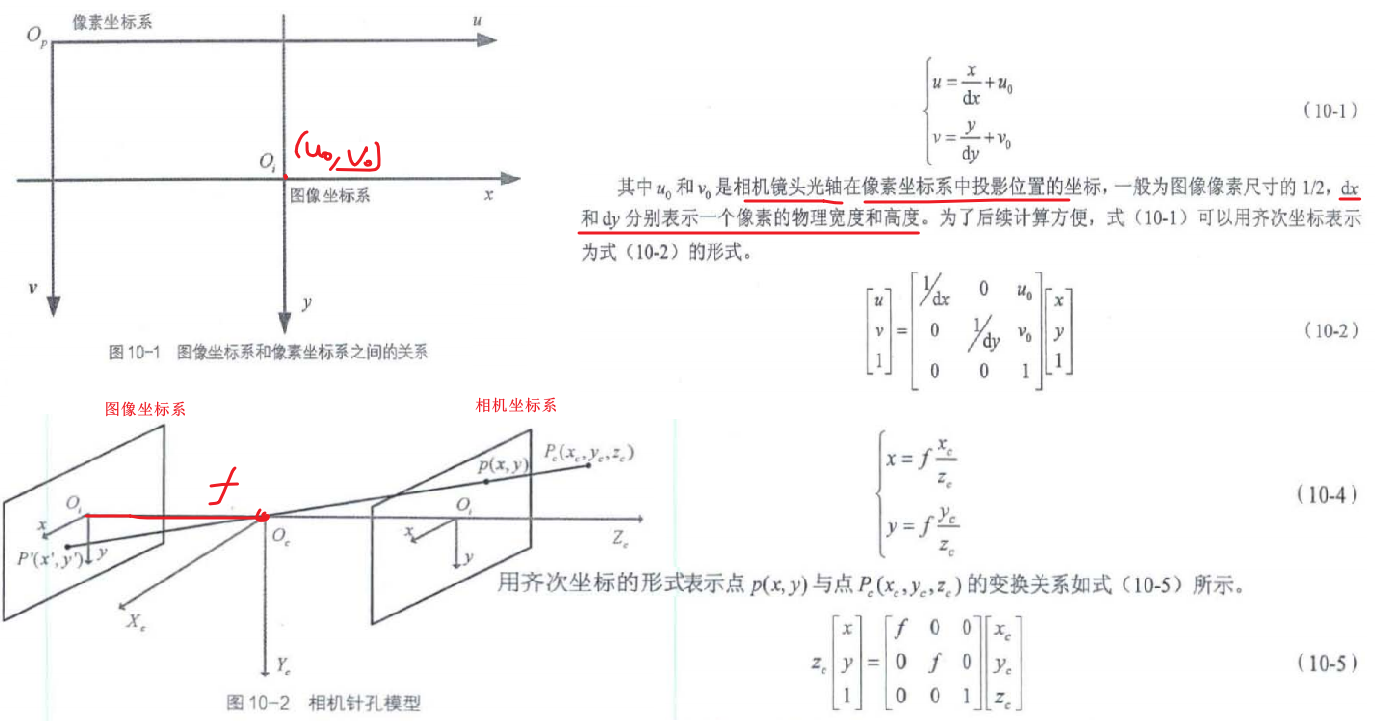
2 为什么要有相机的外参标定？

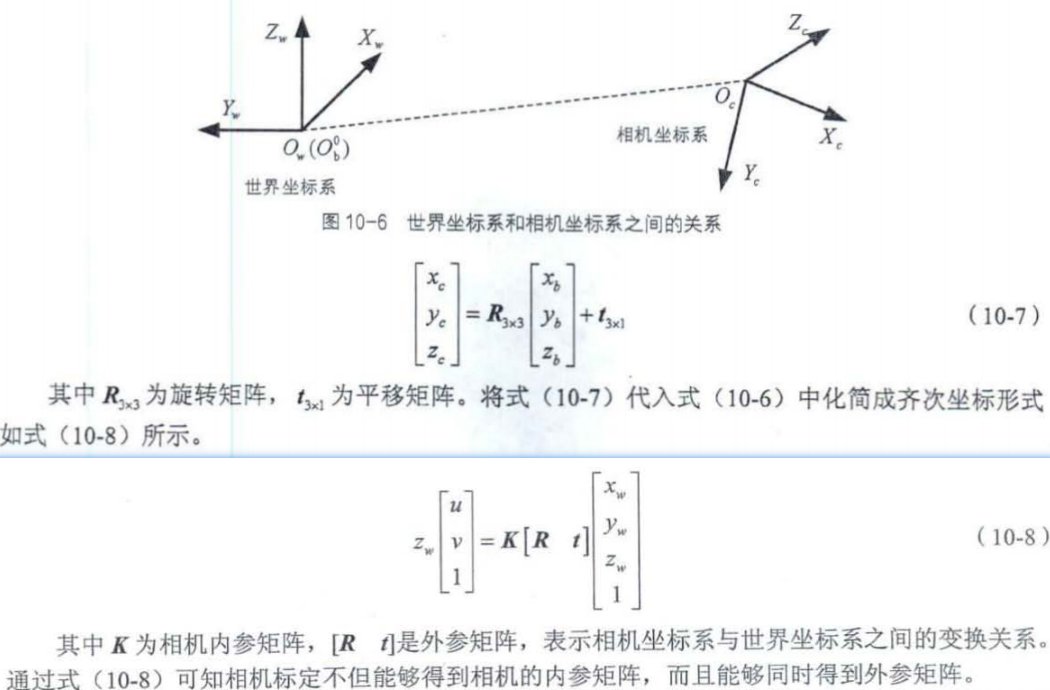
二相机的标定

由相机的成像模型可知，当已知世界坐标系中的三维坐标、图像像素坐标系中二维坐标时，就可以求解相机的内参、外参。接下来介绍OpenCV中的相机标定的相关函数、标定流程、代码及运行结果。

1 OpenCV中的相机标定相关函数介绍

1.1 findChessboardCorners() 函数

1.2 findCirclesGrid() 函数

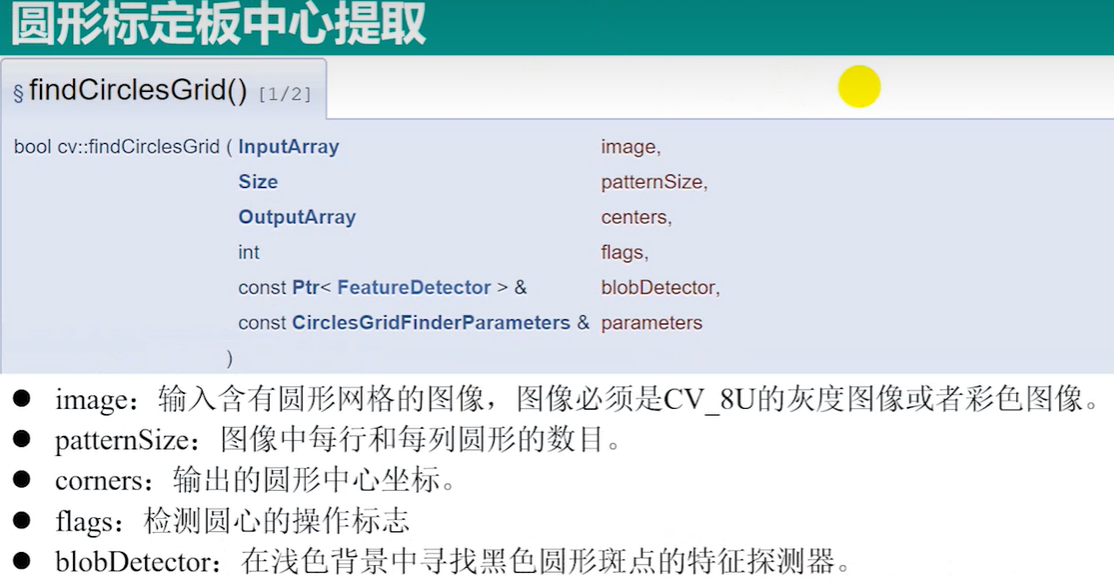
1.3 find4QuadCornerSubpix()函数

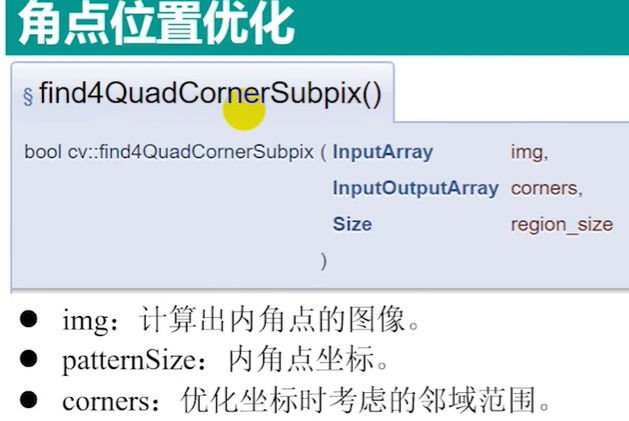
1.4 drawChessboardCorners()函数

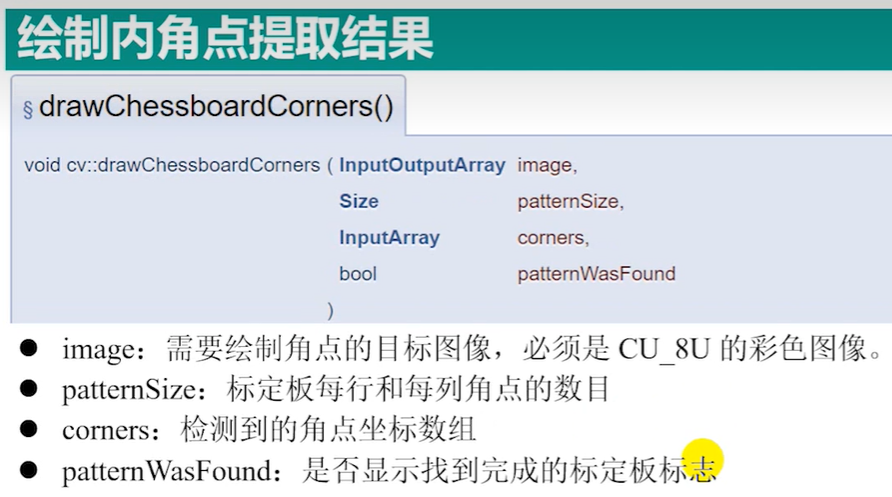
1.5 相机标定函数calibrateCamera()

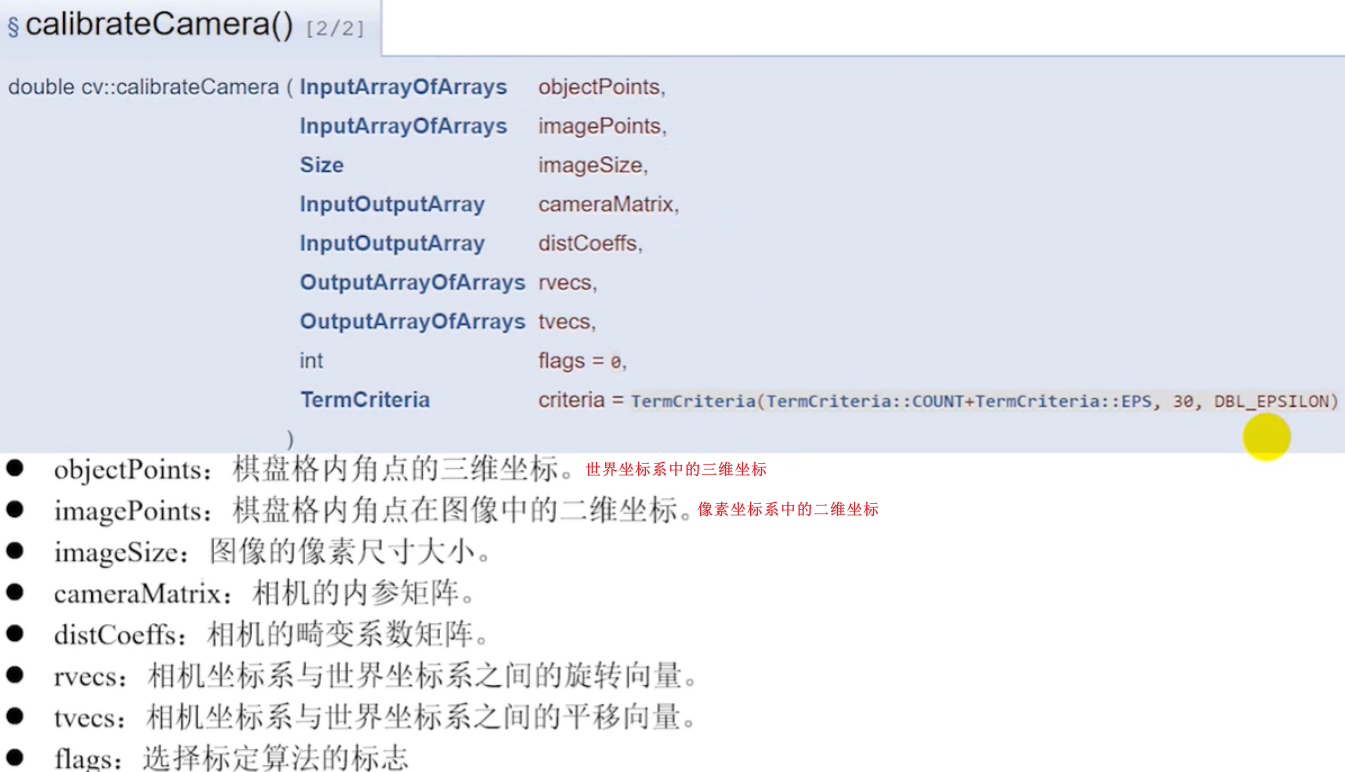
1.6 Rodrigues() 函数

2 相机标定的步骤

选取N张不同角度拍摄的棋盘格图像，使用角点检测得到每张图像上的棋盘像素坐标点；
设定棋盘格中每个方格的物理尺寸和角点的数量，计算世界坐标系中的三维坐标点（z轴设置为0，只需计算x、y轴的坐标）；
调用 calibrateCamera() 获取相机的内参矩阵、畸变系数矩阵、外参中的旋转向量、平移向量；

3 相机标定的代码与运行结果

#include <opencv2\opencv.hpp>
#include <fstream> 
#include <iostream>
#include <vector>

using namespace std;
using namespace cv;

int main()
{
  //读取所有图像
  vector<Mat> imgs;
  string imageName;
  string path = "D:\\zMaterials\\algorithm\\Algo\\Data\\cal\\";
  ifstream fin(path + "calibdata.txt");
  while (getline(fin, imageName))
  {
    Mat img = imread(path + imageName);
    imgs.push_back(img);
  }

  Size board_size = Size(9, 6);  //方格标定板内角点数目（宽，高）
  vector<vector<Point2f>> imgsPoints;
  for (int i = 0; i < imgs.size(); i++)
  {
    Mat img1 = imgs[i];
    Mat gray1;
    cvtColor(img1, gray1, COLOR_BGR2GRAY);
    vector<Point2f> img1_points;
    findChessboardCorners(gray1, board_size, img1_points);  //计算方格标定板角点
    find4QuadCornerSubpix(gray1, img1_points, Size(5, 5));  //细化方格标定板角点坐标
    imgsPoints.push_back(img1_points);
    drawChessboardCorners(img1, board_size, img1_points, true);
    imshow(to_string(i), img1);
    waitKey(0);
  }

  //生成棋盘格每个内角点的空间三维坐标
  Size squareSize = Size(10, 10);  //棋盘格每个方格的真实尺寸
  vector<vector<Point3f>> objectPoints;
  for (int i = 0; i < imgsPoints.size(); i++)
  {
    vector<Point3f> tempPointSet;
    for (int j = 0; j < board_size.height; j++)
    {
      for (int k = 0; k < board_size.width; k++)
      {
        Point3f realPoint;
        // 假设标定板为世界坐标系的z平面，即z=0
        realPoint.x = j * squareSize.width;
        realPoint.y = k * squareSize.height;
        realPoint.z = 0;
        tempPointSet.push_back(realPoint);
      }
    }
    objectPoints.push_back(tempPointSet);
  }

  //图像尺寸
  Size imageSize;
  imageSize.width = imgs[0].cols;
  imageSize.height = imgs[0].rows;

  Mat cameraMatrix = Mat(3, 3, CV_32FC1, Scalar::all(0));  //摄像机内参数矩阵
  Mat distCoeffs = Mat(1, 5, CV_32FC1, Scalar::all(0));  //摄像机的5个畸变系数：k1,k2,p1,p2,k3
  vector<Mat> rvecs;  //每幅图像的旋转向量
  vector<Mat> tvecs;  //每张图像的平移量
  calibrateCamera(objectPoints, imgsPoints, imageSize, cameraMatrix, distCoeffs, rvecs, tvecs, 0);
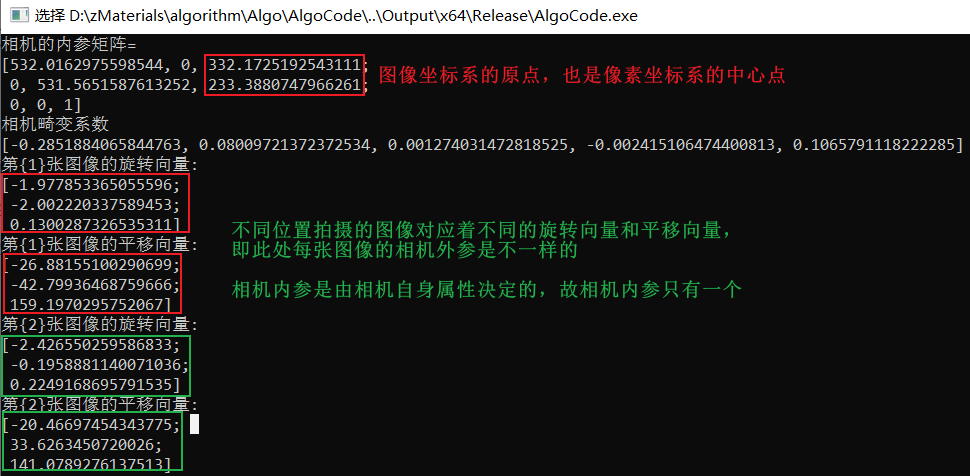
  cout << "相机的内参矩阵=" << endl << cameraMatrix << endl;
  cout << "相机畸变系数" << endl << distCoeffs << endl;
  
  for (int i = 0; i < rvecs.size(); i++)
  {
    //Mat R;
    //Rodrigues(rvecs[i], R);   // 将旋转向量转化为旋转矩阵

    cout << "第{" + to_string(i + 1) + "}张图像的旋转向量:" << endl << rvecs[i] << endl;
    cout << "第{" + to_string(i + 1) + "}张图像的平移向量:" << endl << tvecs[i] << endl;
  }
  waitKey(0);
  destroyAllWindows();

  return 0;
}

运行结果

三相机（图像）校正

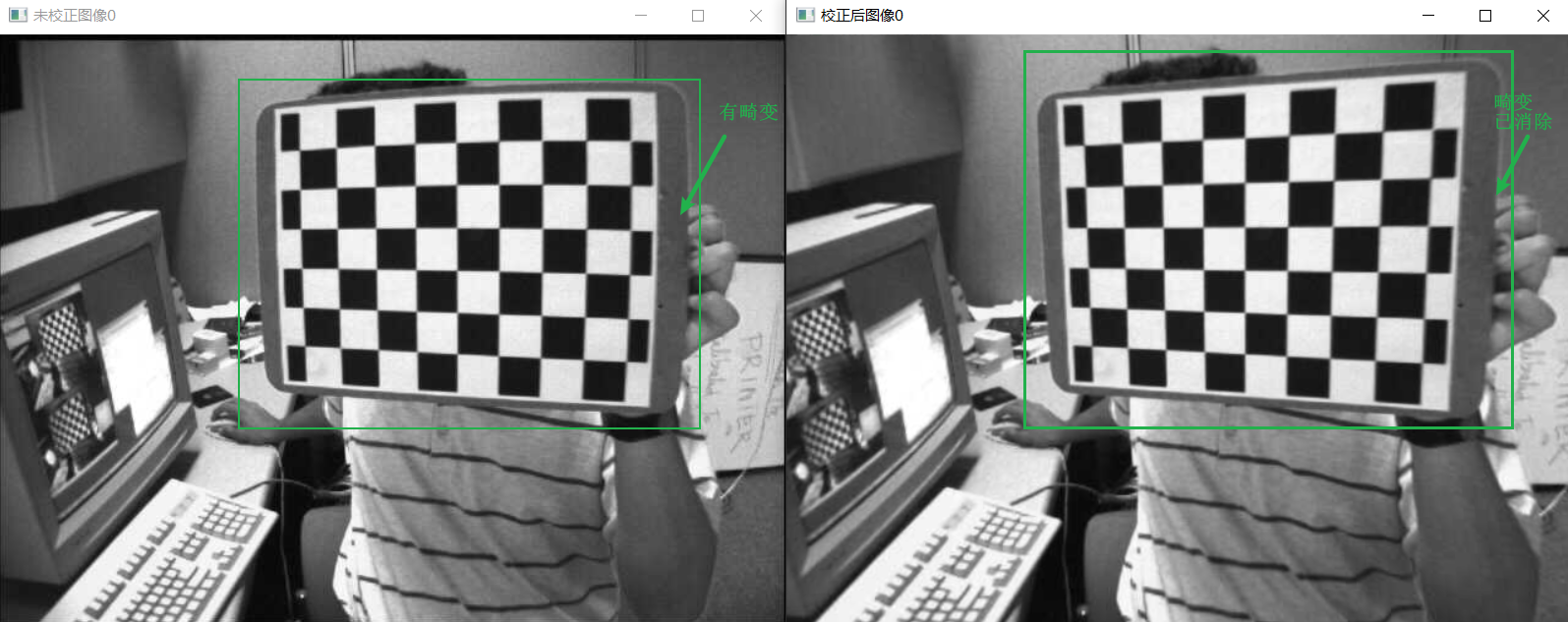
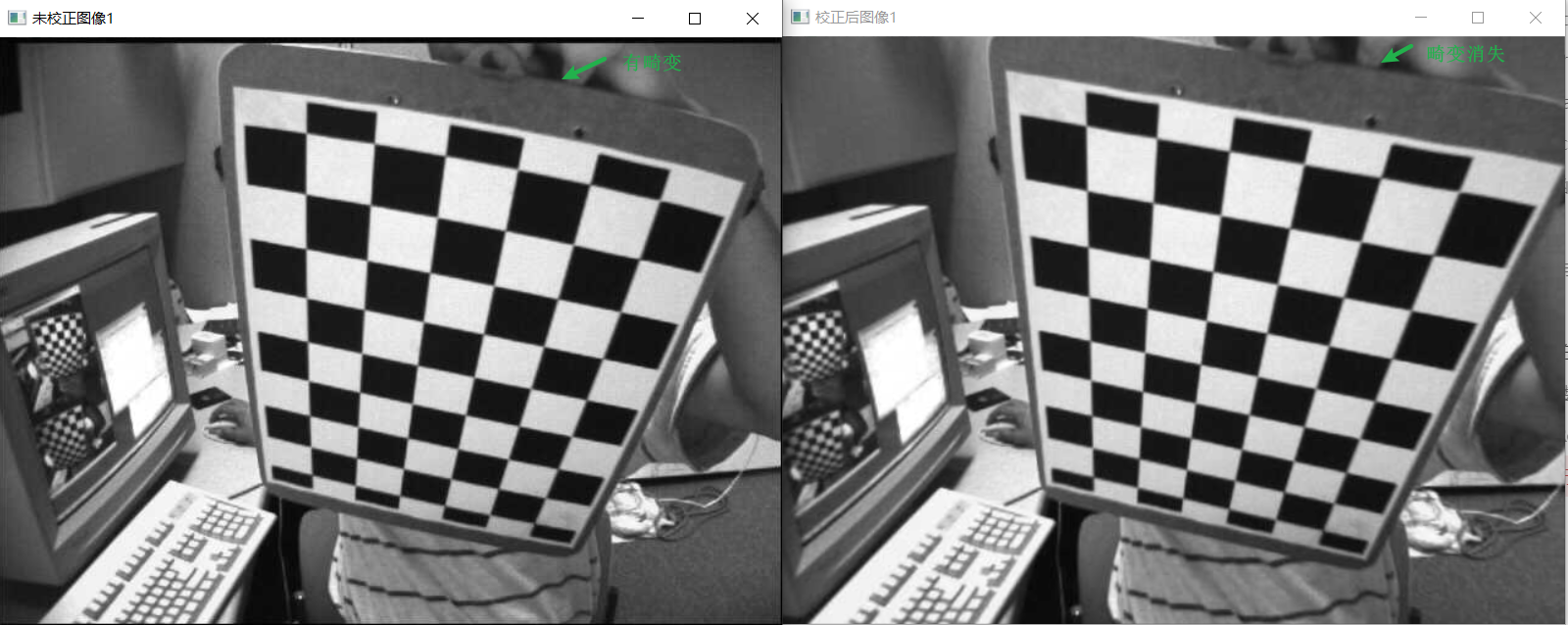
通过标定得到了相机内参矩阵、畸变矩阵，此时可以进行图像校正来去除图像畸变。以下为校正前后的图像：

从图像可以看出，校正前棋盘格的边缘有畸变（曲线），而校正后棋盘格的边缘畸变消失了。

1 OpenCV中去畸变的相关函数

1.1 undistort() 函数

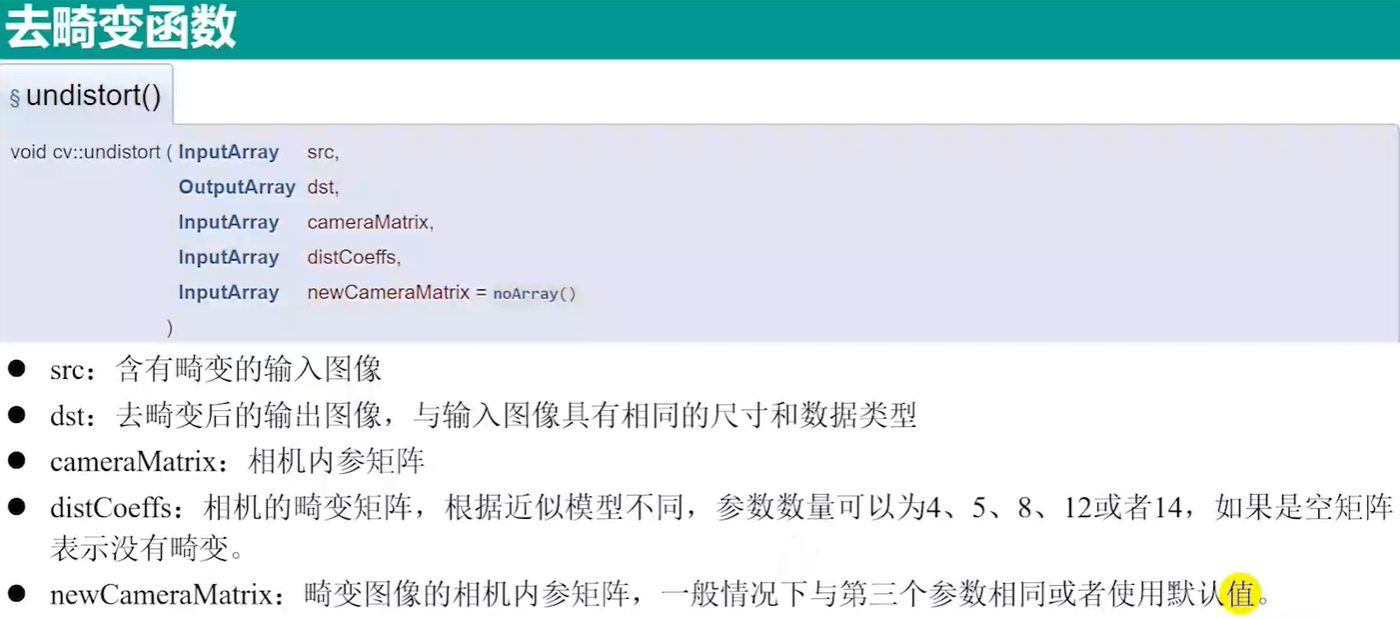
1.2 initUndistortRectifyMap() 和 remap() 函数

2 去畸变的代码及运行结果

#include <opencv2\opencv.hpp>
#include <iostream>
#include <fstream> 
#include <vector>

using namespace std;
using namespace cv;

//使用initUndistortRectifyMap()函数和remap()函数校正图像
void initUndistAndRemap(vector<Mat> imgs,  //所有原图像向量
  Mat cameraMatrix,  //计算得到的相机内参
  Mat distCoeffs,    //计算得到的相机畸变系数
  Size imageSize,    //图像的尺寸
  vector<Mat> &undistImgs)  //校正后的输出图像
{
  //计算映射坐标矩阵
  Mat R = Mat::eye(3, 3, CV_32F);
  Mat mapx = Mat(imageSize, CV_32FC1);
  Mat mapy = Mat(imageSize, CV_32FC1);
  initUndistortRectifyMap(cameraMatrix, distCoeffs, R, cameraMatrix, imageSize, CV_32FC1, mapx, mapy);

  //校正图像
  for (int i = 0; i < imgs.size(); i++)
  {
    Mat undistImg;
    remap(imgs[i], undistImg, mapx, mapy, INTER_LINEAR);
    undistImgs.push_back(undistImg);
  }
}

//用undistort()函数直接计算校正图像
void undist(vector<Mat> imgs,   //所有原图像向量
  Mat cameraMatrix,   //计算得到的相机内参
  Mat distCoeffs,     //计算得到的相机畸变系数
  vector<Mat> &undistImgs)  //校正后的输出图像
{
  for (int i = 0; i < imgs.size(); i++)
  {
    Mat undistImg;
    undistort(imgs[i], undistImg, cameraMatrix, distCoeffs);
    undistImgs.push_back(undistImg);
  }
} 
 
int main()
{
  //读取所有图像
  vector<Mat> imgs;
  string imageName;
  string path = "D:\\zMaterials\\algorithm\\Algo\\Data\\cal\\";
  ifstream fin(path + "calibdata.txt");
  while (getline(fin, imageName))
  {
    Mat img = imread(path + imageName);
    imgs.push_back(img);
  }

  //输入前文计算得到的内参矩阵
  Mat cameraMatrix = (Mat_<float>(3, 3) << 532.016297, 0, 332.172519,
    0, 531.565159, 233.388075,
    0, 0, 1);
  //输入前文计算得到的畸变矩阵
  Mat distCoeffs = (Mat_<float>(1, 5) << -0.285188, 0.080097, 0.001274, -0.002415, 0.106579);
  vector<Mat> undistImgs;
  Size imageSize;
  imageSize.width = imgs[0].cols;
  imageSize.height = imgs[0].rows;

  //使用initUndistortRectifyMap()函数和remap()函数校正图像
  initUndistAndRemap(imgs, cameraMatrix, distCoeffs, imageSize, undistImgs);

  //用undistort()函数直接计算校正图像，下一行代码取消注释即可
  //undist(imgs, cameraMatrix, distCoeffs, undistImgs);

  //显示校正前后的图像
  for (int i = 0; i < imgs.size(); i++)
  {
    string windowNumber = to_string(i);
    imshow("未校正图像" + windowNumber, imgs[i]);
    imshow("校正后图像" + windowNumber, undistImgs[i]);
  }

  waitKey(0);
  return 0;
}

运行结果

四相机投影

单目投影是指根据相机的成像模型计算空间中三维坐标点在图像二维平面中坐标的过程。OpenCV4 中提供 projectPoints() 函数用于计算世界坐标系中的三维点投影到像素坐标系中的二维坐标。

在单目投影时，需要提供三维点在世界坐标系中的坐标、世界坐标系变换到相机坐标系的旋转向量和平移向量以及相机的内参矩阵和畸变矩阵。

1 OpenCV中projectPoints()函数

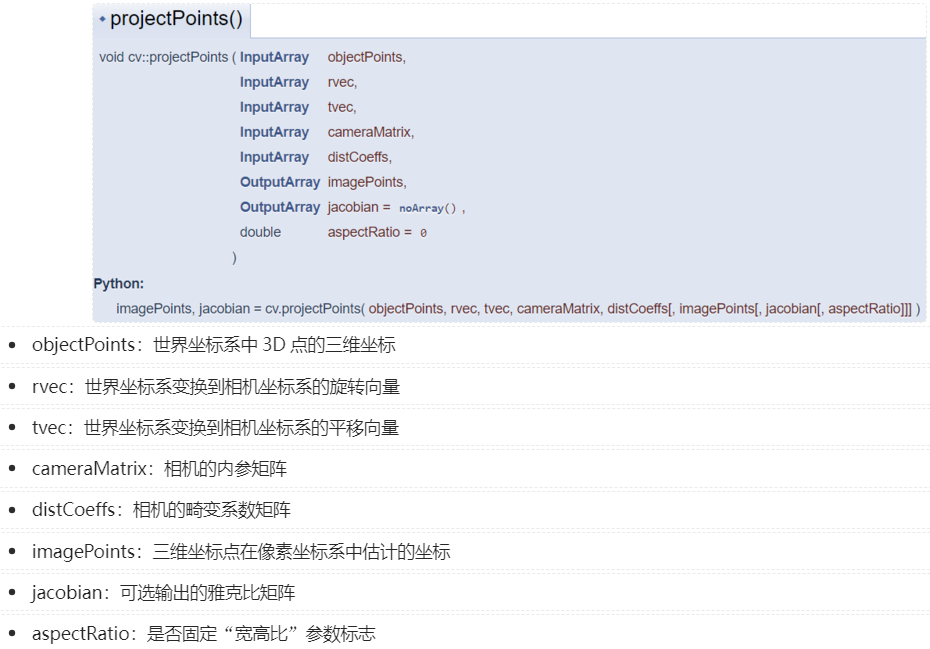
2 单目投影代码和运行结果

#include "opencv2/opencv.hpp"
#include <iostream>
#include <vector>

using namespace std;
using namespace cv;

int main()
{
  /***************各项参数都是标定时得到的*****************/

  //输入前文计算得到的内参矩阵和畸变矩阵
  Mat cameraMatrix = (Mat_<float>(3, 3) << 532.016297, 0, 332.172519,
                                         0, 531.565159, 233.388075,
                                         0, 0, 1);
  Mat distCoeffs = (Mat_<float>(1, 5) << -0.285188, 0.080097, 0.001274,
                                           - 0.002415, 0.106579);
  //第一张图像相机坐标系与世界坐标系之间的关系
  //Mat rvec = (Mat_<float>(1, 3) <<-1.977853, -2.002220, 0.130029);
  //Mat tvec = (Mat_<float>(1, 3) << -26.88155,-42.79936, 159.19703);
  //第二张图像相机坐标系与世界坐标系之间的关系
  Mat rvec = (Mat_<float>(1, 3) << -2.4266, -0.1959, 0.2249);
  Mat tvec = (Mat_<float>(1, 3) << -20.467, 33.626, 141.08);

  //生成第一张图像中内角点的三维世界坐标
  Size boardSize = Size(9, 6);
  Size squareSize = Size(10, 10);  //棋盘格每个方格的真实尺寸
  vector<Point3f> PointSets;
  for (int j = 0; j < boardSize.height; j++)
  {
    for (int k = 0; k < boardSize.width; k++)
    {
      Point3f realPoint;
      // 假设标定板为世界坐标系的z平面，即z=0
      realPoint.x = j*squareSize.width;
      realPoint.y = k*squareSize.height;
      realPoint.z = 0;
      PointSets.push_back(realPoint);
    }
  }
  
  //根据三维坐标、相机与世界坐标系间的关系（旋转、平移）、内参、畸变参数 来估计内角点像素坐标
  vector<Point2f> imagePoints;
  projectPoints(PointSets, rvec, tvec, cameraMatrix, distCoeffs, imagePoints);


  /***********计算图像中内角点的真实坐标误差******************/
  string path = "D:\\zMaterials\\algorithm\\Algo\\Data\\cal\\left02.jpg";
  Mat img = imread(path);
  Mat gray;
  cvtColor(img, gray, COLOR_BGR2GRAY);
  vector<Point2f> imgPoints;
  findChessboardCorners(gray, boardSize, imgPoints);  //计算方格标定板角点
  find4QuadCornerSubpix(gray, imgPoints, Size(5, 5));  //细化方格标定板角点坐标

  //计算估计值和图像中计算的真实时之间的平均误差
  float e = 0;
  for (int i = 0; i < imagePoints.size(); i++)
  {
    float eX = pow(imagePoints[i].x - imgPoints[i].x, 2);
    float eY = pow(imagePoints[i].y - imgPoints[i].y, 2);
    e = e + sqrt(eX + eY);
  }
  e = e / imagePoints.size();
  cout << "估计坐标与真实坐标之间的误差" << e << endl;
  waitKey(0);
  return 0;
}

运行结果：通过成像模型的内外参评估后的像素坐标系中二维坐标的误差很小。

posted @ 2024-01-10 20:14 PRO_Z 阅读(1059) 评论(0) 编辑收藏举报

刷新页面返回顶部