互信息与相关性的图像配准
一 基于互信息与相关性的图像配准
1 互信息定义及图像配准
互信息定义如下:
\[MI(X;Y) = \sum\limits_{x}\sum\limits_{y}p_{(X,Y)}(x,y)\log\cfrac{p_{(X,Y)}(x,y)}{{p_X(x)}\cdot{p_Y(y)}}
\]
从定义中可以看出,当X和Y两个变量趋近于独立时,
\[p_{(X,Y)}(x,y)={p_X(x)}\cdot{p_Y(y)}
\]
此时,
\[\log\cfrac{p_{(X,Y)}(x,y)}{{p_X(x)}\cdot{p_Y(y)}}\approx 0,MI(X;Y)有最小值。
\]
反之,若X和Y两个变量越相关,
\[MI(X;Y)则越大。
\]
基于以上理论,设有模板图片fixed、待配准图片moving,若
\[fixed ( x , y ) = moving( x − △ x , y − △ y )
\]
则当moving平移 △x、 △y 时,以fixed、moving图像二维亮度直方图(表示联合分布)作为输入,求得的互信息MI有最大值。
2 相关性的定义及图像配准
皮尔逊相关系数:
\[ ρX,Y=\cfrac{cov(X,Y)}{σXσY}=\cfrac{[(X−μX)(Y−μY)]}{σXσYE}
\]
\[ρX,Y =\cfrac{\sum\limits_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{{\sum\limits_{i=1}^n(x_i-\bar{x}} )^2}\sqrt{{\sum\limits_{i=1}^n(y_i-\bar{y}} )^2}}\\ \\ \quad\quad\ = \cfrac{n\sum x_iy_i-\sum x_i \sum y_i}{\sqrt{n \sum x_i^2-(\sum x_i)^2}\sqrt{n \sum y_i^2-(\sum y_i)^2}}
\]
基于以上理论,设有模板图片fixed、待配准图片moving,若
\[fixed ( x , y ) = moving( x − △ x , y − △ y )
\]
则当moving平移 △x、 △y 时,将fixed、moving图像按照一维数据排列,进行相关性计算,求得的相关性有最大值;相关性越接近1,配准效果越好,反之,相关性越接近0,配准效果越差。
二 模板图像fixed、(待)配准图像moving的可视化
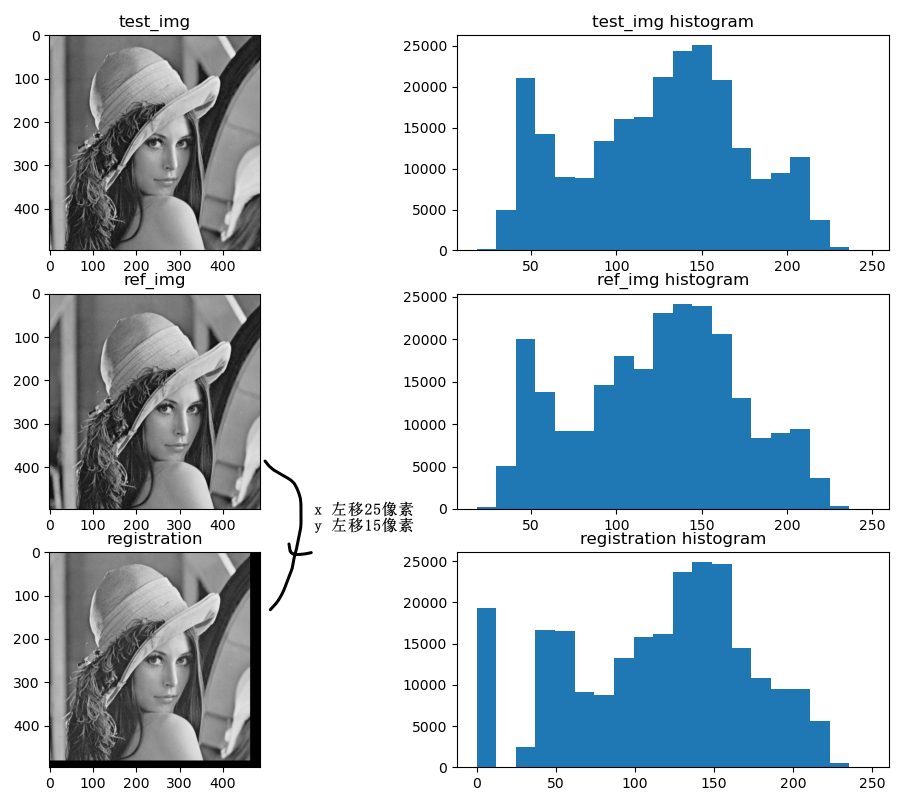
1 fixed 和 moving 图像的直方图
注:配准后图像的缺失边界可以用fixed图像对应的像素来填充,这样差分图对应的像素值就为0。
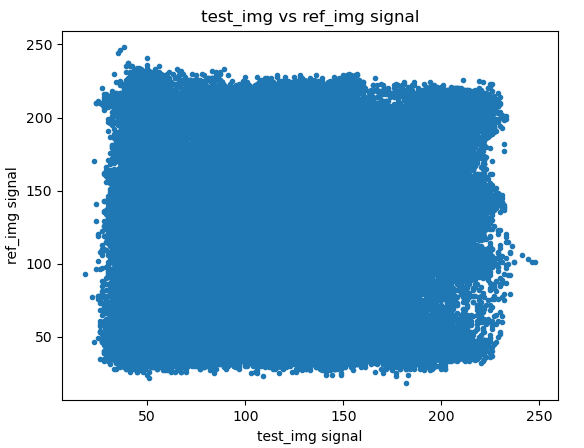
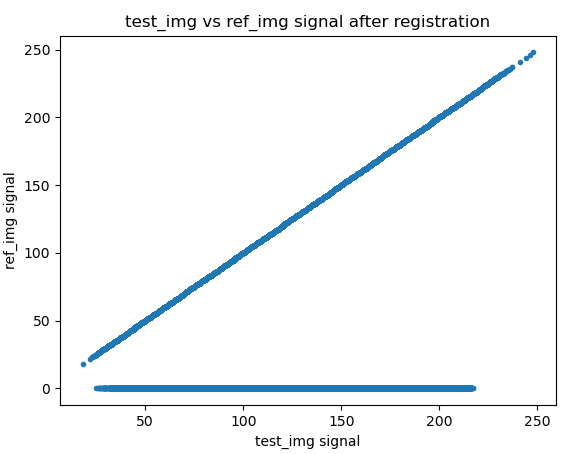
2 fixed 和 moving 图像的散点图
从散点图上可以看出,fixed 和 待配准的 moving 图像的像素分布是相互独立的,而fixed 和 配准的 moving 图像的像素分布表现出一定的线性关系。
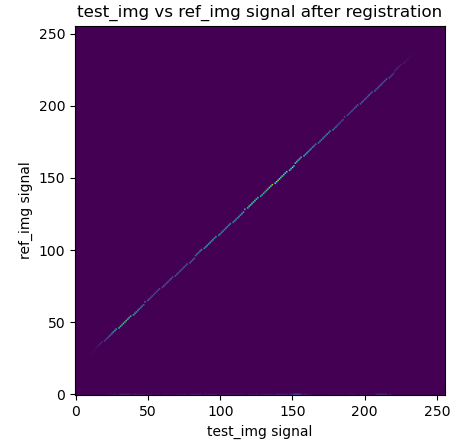
3 fixed 和 moving 图像的2D直方图
同样,从2D直方图上可以看出,fixed 和 待配准的 moving 图像的像素分布线性度不好,而fixed 和 配准的 moving 图像的像素分布表现出一定的线性关系。。
4 fixed 和 moving 图像的差分图
三 图像配准的代码
def mutual_information(hgram):
""" Mutual information for joint histogram
"""
# Convert bins counts to probability values
pxy = hgram / float(np.sum(hgram))
px = np.sum(pxy, axis=1) # marginal for x over y
py = np.sum(pxy, axis=0) # marginal for y over x
px_py = px[:, None] * py[None, :] # Broadcast to multiply marginals
nzs = pxy > 0 # Only non-zero pxy values contribute to the sum
return np.sum(pxy[nzs] * np.log2(pxy[nzs] / px_py[nzs]))
def correlation_information(img_fixed, img_moved):
def NCC(img1, img2):
# # 图片2的标准差
# print(np.std(img2))
# 相关系数,这里使用的是有偏估计
# 协方差 Cov(X, Y) = Σ((Xᵢ - μₓ)(Yᵢ - μᵧ)) / n
# 方差 D(X) = (∑(x - μ)²) / n
# R = Con(X, Y) / (sqrt(D(X)) * sqrt(D(Y)))
con = np.mean(np.multiply((img1 - np.mean(img1)), (img2 - np.mean(img2)))) # 协方差
img1Std = np.std(img1)
img2Std = np.std(img2)
NCCValue = con / (img1Std * img2Std)
return NCCValue
r, _ = stats.pearsonr(img_fixed.ravel(), img_moved.ravel())
# ncc_cal_in = np.corrcoef(img_fixed.astype(np.float32).flatten(), img_moved.astype(np.float32).flatten())[0][1]
# ncc_cal = NCC(img_fixed, img_moved)
# print(r, ncc_cal_in, ncc_cal)
return r
METHOD_REGISTRATION_MI = 0
METHOD_REGISTRATION_CI = 1
def ImageRegistration(img_fixed, img_moved, max_offset_XY=(5, 5), method=METHOD_REGISTRATION_MI):
large = -np.inf
large_ij = []
h, w = img_moved.shape[:2]
ox, oy = max_offset_XY
dirs = [(-1, -1), (-1, 1), (1, 1), (1, -1)]
for i in range(oy):
for j in range(ox):
if i == 0 and j == 0:
ret = 0
if method == METHOD_REGISTRATION_MI:
hist_2d_moved, x_edges, y_edges = np.histogram2d(
img_fixed.ravel(),
img_moved.ravel(),
bins=255, range=[[0, 255], [0, 255]])
ret = mutual_information(hist_2d_moved)
if method == METHOD_REGISTRATION_CI:
ret = correlation_information(img_fixed, img_moved)
if ret > large:
large = ret
large_ij = [i, j]
continue
for _dir in dirs:
deltaY = i * _dir[1]
deltaX = j * _dir[0]
M = np.array([[1, 0, deltaX], [0, 1, deltaY]], dtype=np.float)
img_moved_modify = cv2.warpAffine(img_moved, M, dsize=(w, h))
ret = 0
if method == METHOD_REGISTRATION_MI:
hist_2d_moved, x_edges, y_edges = np.histogram2d(
img_fixed.ravel(),
img_moved_modify.ravel(),
bins=256, range=[[0, 255], [0, 255]])
ret = mutual_information(hist_2d_moved)
if method == METHOD_REGISTRATION_CI:
ret = correlation_information(img_fixed, img_moved_modify)
if ret > large:
large = ret
large_ij = [deltaY, deltaX]
offset_y, offset_x = large_ij
print("ret = {}, offset_y = {}, offset_x = {} pixel".format(large, offset_y, offset_x))
M = np.array([[1, 0, offset_x], [0, 1, offset_y]], dtype=np.float)
img_moved_final = cv2.warpAffine(img_moved, M, dsize=(w, h))
return img_moved_final, offset_x, offset_y