直方图均衡化原理与实现
一 直方图均衡化的概念
直方图均衡化(Histogram Equalization)是一种**增强图像对比度**(Image Contrast)的方法,其主要思想是将一副图像的**灰度直方图分布**通过**累积分布函数**变成**近似均匀分布**(直观上在某个灰阶范围内像素值保持一致 ),从而增强图像的对比度。为了将原图像的亮度范围进行扩展, 需要一个映射函数, 将原图像的像素值均衡映射到新直方图中。
问题1:为什么选择累计分布函数?
均衡化过程中,必须要保证两个条件:①像素无论怎么映射,一定要保证原来的大小关系不变,较亮的区域,依旧是较亮的,较暗依旧暗,只是对比度增大,绝对不能明暗颠倒;②如果是8位图像,那么像素映射函数的值域应在0和255之间的,不能越界。综合以上两个条件,累积分布函数是个好的选择,因为累积分布函数是单调增函数(控制大小关系),并且值域是0到1(控制越界问题),所以直方图均衡化中使用的是累积分布函数。
问题2:为什么使用累积分布函数处理后像素值会均匀分布?
对于概率分布函数和累积分布函数,前者的二维图像的灰度直方图是参差不齐的,后者因为人眼视觉系统(HVS),会将小范围内的像素值认为是同一个像素值,即在某个灰阶范围内像素值保持一致,故后者的二维图像的灰度直方图呈现均匀分布;
二 直方图均衡化的原理
假设图像中像素的总数是 N,图像的灰度级数是 L,灰度级空间是[0, L-1],用𝑛_𝑘表示第 k 级灰度(第 k 个灰度级,像素值为 k)在图像内的像素点个数,那么该图像中灰度级为𝑟_𝑘(第 k 个灰度级)出现的概率为:
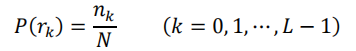
根据灰度级概率,对其进行均衡化处理的计算公式为:
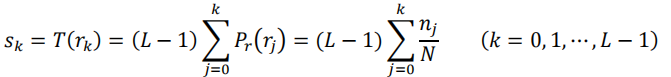
\[式中,\sum_{j=0}^{k} P_{r}\left(r_{j}\right)表示累计概率,将该值与灰度级的最大值 L-1 相乘即得到均衡化后的新灰度级(像素值)
\]
三 直方图均衡化的求解过程
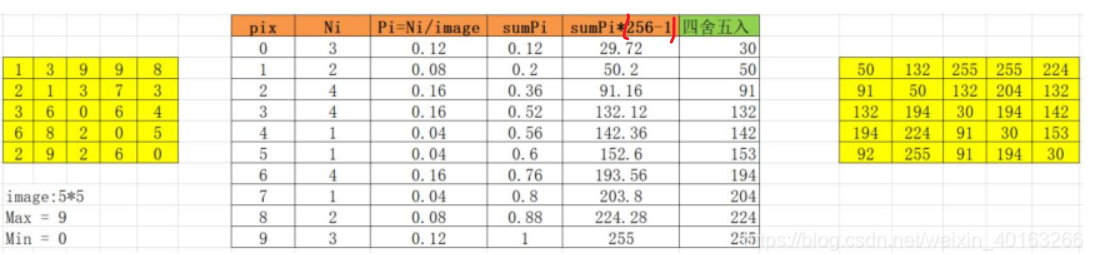
求解步骤:
- 求输入图像的灰度直方图
- 对灰度直方图进行归一化,即概率直方图
- 求累计概率直方图(累计分布函数),记作 Trans
- 通过 均衡化原理 将 源输入图像的像素值 映射到 均衡化后的图像像素值中去
参考链接:https://blog.csdn.net/weixin_40163266/article/details/113802909,注:求出Trans后,将图像映射到8位位图(0~255),是 Trans * 255
四 直方图均衡化的代码及结果分析
核心代码:
def histCalc(img):
"""
灰度直方图统计
:param img: 灰度图
:return: 直方图
"""
hist = np.zeros(256)
rows = img.shape[0]
cols = img.shape[1]
for i in range(rows):
for j in range(cols):
tmp = img[i][j]
hist[tmp] = hist[tmp] + 1
print(hist.shape)
return hist
def histEqualize(img):
"""
直方图均衡化
:param img: 灰度图
:return: 均衡化的图像
"""
hist = histCalc(img)
imgH, imgW = img.shape[0], img.shape[1]
allPixel = imgH * imgW
# 计算累计分布函数(变换函数)
trans = hist / allPixel * 255
for i in range(1, len(trans)):
trans[i] = trans[i] + trans[i-1]
# 均衡化后的图像
imageEqualize = img.copy()
for i in range(imgH):
for j in range(imgW):
imageEqualize[i][j] = trans[img[i][j]]
return imageEqualize
运行结果:
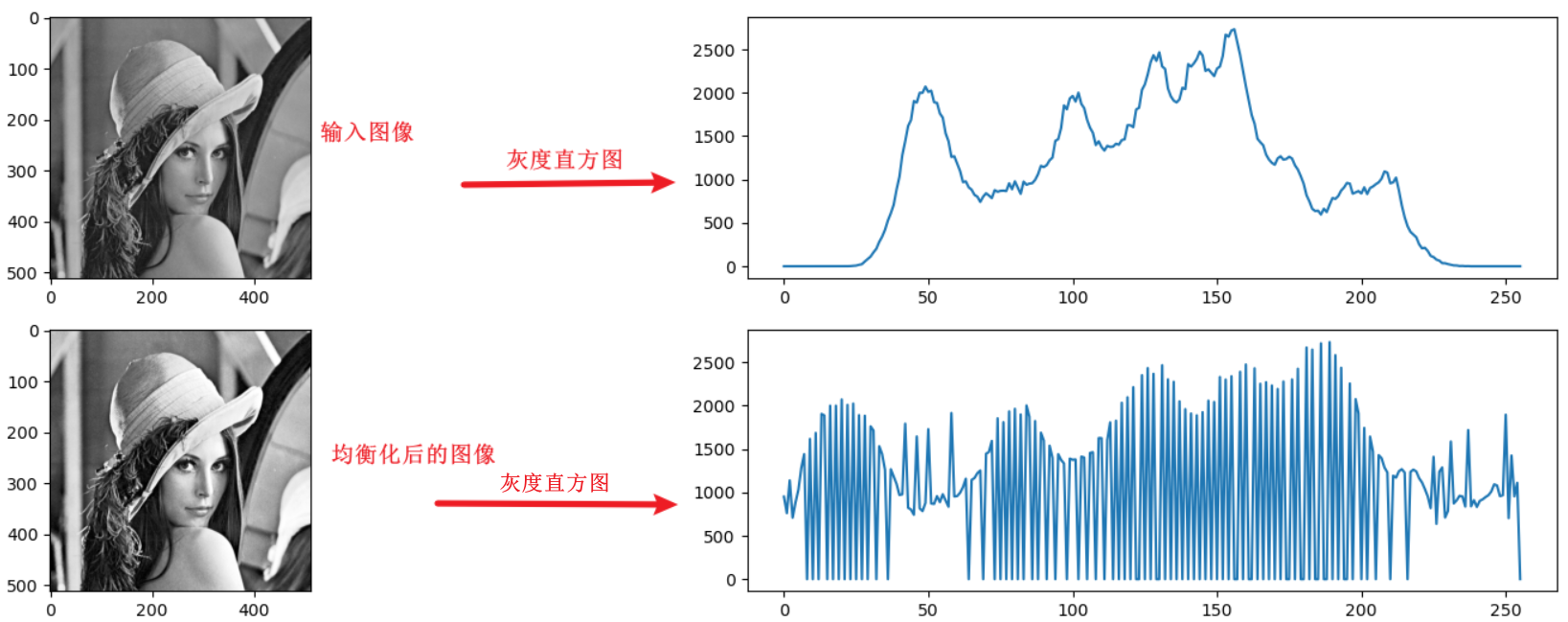
结果分析:输入图像中没有较暗、较亮的像素值,经过均衡化后,输入图像中的较暗、较亮的图像区域得到了有效改善。
五 二维直方图
numpy中的histogram2d 函数 说明
def histogram2d(x, y, bins=10, range=None, normed=None, weights=None, density=None):
"""
Compute the bi-dimensional histogram of two data samples.
Parameters
----------
x : array_like, shape (N,), nx = N
直方图中的Y轴坐标
y : array_like, shape (N,), ny = N
直方图中的X轴坐标
bins : int or [int, int],直方图X轴和Y轴坐标的分组;若是int,对X轴和Y轴同时生效;若是[int, int],对X轴、Y轴分别设置;
range:shape(2,2), default ``[[xmin, xmax], [ymin, ymax]]``, x 轴 和 y 轴的坐标的取值范围
Returns
-------
H : ndarray, shape(nx, ny)
The bi-dimensional histogram of samples `x` and `y`.
xedges : ndarray, shape(nx+1,)
The bin edges along the first dimension. y 轴不同bin分组的边界,最后一个bin边界为左闭右闭,其它为左开右闭
yedges : ndarray, shape(ny+1,)
The bin edges along the second dimension.x 轴不同bin分组的边界,最后一个bin边界为左闭右闭,其它为左开右闭
"""
import numpy as np
ref_img = np.random.randint(0, 11, size=(3, 4))
test_img = np.random.randint(0, 11, size=(3, 4))
print("ref_img\n", ref_img.ravel())
print("test_img\n", test_img.ravel())
hist_2d, x_edges, y_edges = np.histogram2d(ref_img.ravel(), test_img.ravel(), bins=10, range=((0, 10), (0, 10)))
print(hist_2d)
print("\n ----")
print(x_edges)
print("\n ----")
print(y_edges)
"""
ref_img: [1 3 4 8 6 7 9 4 1 5 0 2]
test_img: [1 0 8 7 10 9 4 1 6 10 2 6]
hist_2d
[[0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0. 1. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]
[1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0. 0. 0. 1. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
[0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
[0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]]
x_edges: [ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.]
y_edges: [ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.]
"""
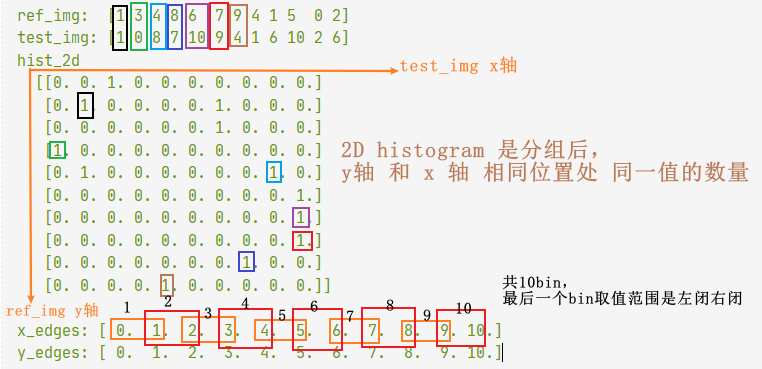
二维直方图 可以用来计算互信息,见图像配准系列;
