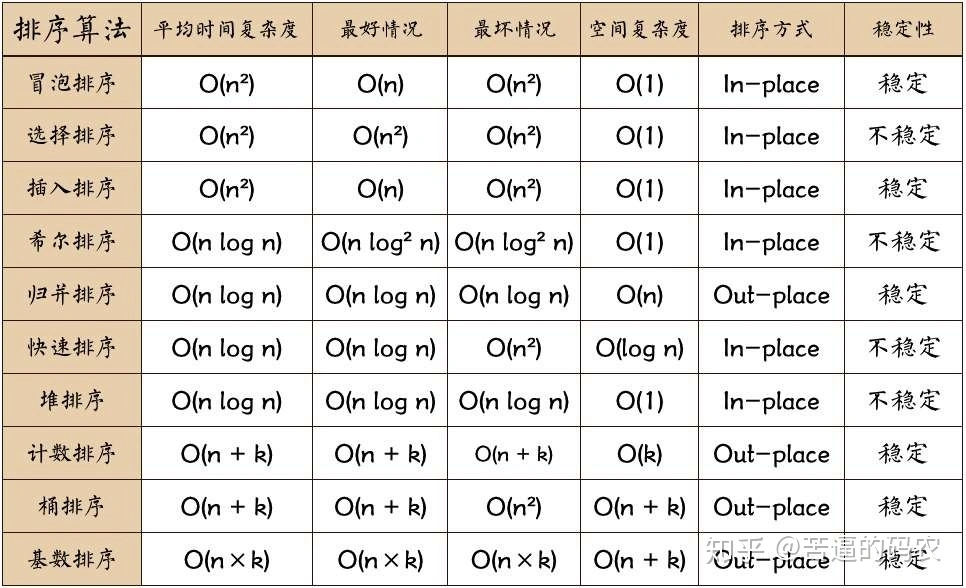
排序算法归纳

1 排序算法的分类

1.1 稳定排序 vs 非稳定排序

  • 稳定排序：对于相同值的元素在序列排序前后的相对位置保持一致，即如果Ai = Aj，Ai原来在Aj位置前，排序后Ai还是要在Aj位置前。如 插入排序、冒泡排序、归并排序。
  • 不稳定排序：对于相同值的元素在序列排序前后的相对位置不一定保持一致，如选择排序、快排、堆排序。
  • 注：对于不同值的元素，稳定排序与不稳定排序效果是一样的。

1.2 内部排序 VS 外部排序

  • 内部排序：将待排序的数据一次性读入内存进行排序；
  • 外部排序：当待排序的数据非常大时，即不能将数据一次性读入内存，需要借助外存并通过内存来对数据排序。

2 选择排序

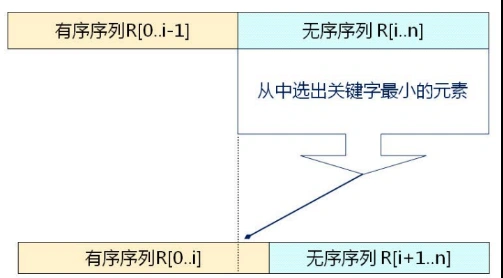
2.1 思想

  • 每次（例如第i次，i=0，1，2，... ，n-2）从后面的n-i 个待排序的数据元素中选出关键字最小的元素，做为有序元素序列的第i个元素。
  • 第i次排序示例：

2.2 代码实现

void select_sort(int *num, int n) {
    for (int i = 0; i < n - 1; i++) {
        int ind = i;    // 最小值的索引
        for (int j = i + 1; j < n; j++) {
            if (num[j] < num[ind]) ind = j;
        }
        // ind != i 说明找到了新的最小值元素索引
        if (ind != i) swap(num[i], num[ind]);
    }
    return ;
}

3 插入排序

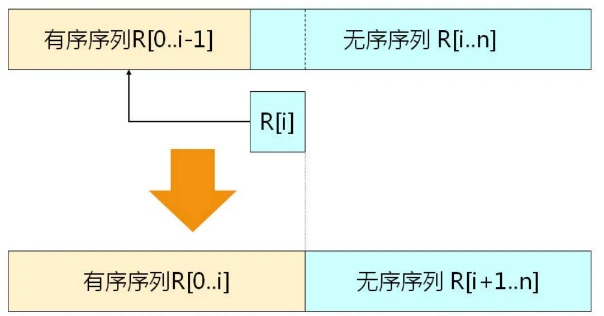
3.1 思想

  • 当插入第 i (i≥1)个数据元素时，前面的V[0]，V[1]，... , V[i-1]已经排好序；这时，用V[i]的关键字与V[i-1]、V[i-2]，... , V[0]的关键字进行比较，找到位置后将V[i]插入，原来位置上的对象向后顺移。
  • 插入第i个元素的示例：

3.2 代码实现

void insert_sort(int *arr, int len) {
    for (int i = 1; i < len; i++) {
        int k = i;
        int v = arr[i];
        for (int j = i - 1; (j >= 0) && (v < arr[j]); j--) {
                arr[j + 1] = arr[j];
                k = j;
        }
        if (k != i) arr[k] = v;
    }
    return ;
}

4 冒泡排序

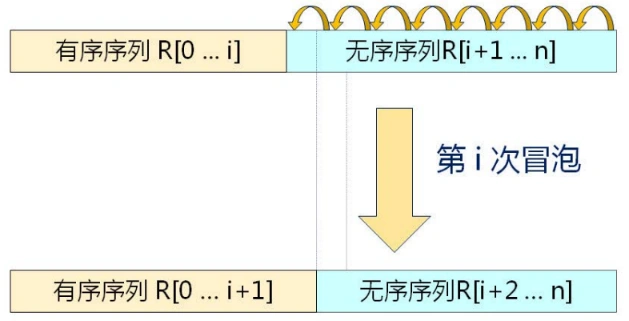
4.1 思想

  • 每次从后向前进行（假设为第i次），j=n-1，n-2，...，i，两两比较V[j-1] 和 V[j]的关键字；如果发生逆序，则交换V[j-1] 和 V[j]；
  • 注：冒泡排序算法中，如果某一次的冒泡过程中无元素交换操作，说明此时的序列已经是有序序列了，应该提前结束；（优化手段）
  • 第i次冒泡示例：

4.2 代码实现

void bubble_sort(int* arr, int len) {
    int exchange = 1;
    for (int i = 0; (i < len) && exchange; i++) {
        exchange = 0;
        for (int j = len - 1; j > i; j--) {
            if (arr[j] < arr[j - 1]) {
                swap(arr[j], arr[j - 1]);
                exchange = 1;
            }
        }
    }
    return ;
}

5 希尔排序

5.1 思想

  • 将待排序序列划分为若干组，在每一组内进行插入排序，以使整个序列基本有序，然后再对整个序列进行插入排序；

5.2 代码实现

void Shell(int* arr, int len) {
    int d = len;
    do {
        d = d / 3 + 1;
        for (int i = d; i < len; i += d) {
            int k = i;
            int v = arr[i];
            for (int j = i - d; (j >= 0) && (v < arr[j]); j -= d) {
                arr[j + d] = arr[j];
                k = j;
            }
            if (k != i) arr[k] = v;
        }
    } while (d > 1);
    return ;
}

6 归并排序

6.1 思想

  • 将两个有序序列合并成一个新的有序序列，这种归并方法称为2路归并，其时间复杂度为\(O(n*log_2n)\)；
  • 归并的套路：
    • 将3个有序序列归并为一个新的有序序列，称为3路归并；
    • 将N个有序序列归并为一个新的有序序列，称为N路归并；
    • 将多个有序序列归并为一个新的有序序列，称为多路归并；
  • 2路归并的示例展示：

6.2 代码实现

void merge_sort(int* arr, int l, int r) {
    if (r == l) return; // 递归出口

    // 二路归并
    int mid = l + (r - l) / 2;
    merge_sort(arr, l, mid);
    merge_sort(arr, mid + 1, r);
    // 左右数组合并->拷贝
    int* temp = (int*)malloc(sizeof(int) * (r - l + 1));
    int p1 = l, p2 = mid + 1, p = 0;    // p1：左侧数据第1个元素的下标，p2：右侧数据第1个元素的下标
    while (p1 <= mid || p2 <= r) {
        // p2 > r：右侧数组元素遍历结束
        if (p2 > r || (p1 <= mid && arr[p1] <= arr[p2])) {
            temp[p++] = arr[p1++];
        } else {
            temp[p++] = arr[p2++];
        }
    }
    memcpy(arr + l, temp, sizeof(int) * (r - l + 1));
    free(temp);

    return ;
}

7 快速排序

7.1 思想

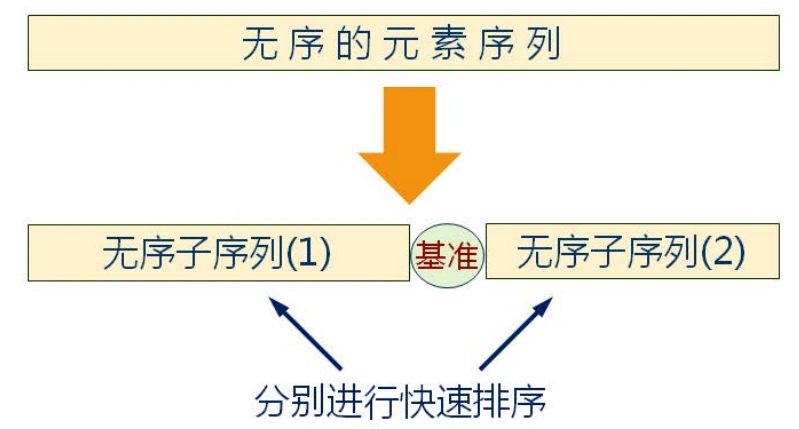
  • 任取序列中的某个元素作为基准，将整个序列划分为左右两个子序列；
    • 左侧子序列中的所有元素都小于或等于基准元素，右侧子序列中的所有元素都大于基准元素；（升序排序）
    • 基准元素排在这两个子序列中间；
  • 分别对这两个子序列重复进行划分，直到所有的数据元素都排列在相应位置上为止；（递归实现）
  • 快排示例：

7.2 代码实现

void quick_sort(int *num, int l, int r) {
    if (l >= r) return ;
    int x = l, y = r, z = num[x];   // x：头指针的位置；y：尾指针的位置；z：主元，默认为待排序数组的第一个元素
    while (x < y) {
        while (x < y && num[y] > z) y--;
        if (x < y) num[x++] = num[y];
        while (x < y && num[x] < z) x++;
        if (x < y) num[y--] = num[x];
    }
    num[x] = z;
    quick_sort(num, l, x - 1);
    quick_sort(num, x + 1, r);
    return ;
}

8 排序算法归纳

posted @ 2022-03-09 17:36  PRO_Z  阅读(49)  评论(0)  编辑  收藏  举报