链表
1 底层存储结构
-
顺序表需要一块连续的内存空间 来存储, 对内存的要求比较高。如果我们申请一个 100MB 大小的顺序表,当内存中没有连续的、足够大的存储空间时,即便内存的剩余总可用空间大于 100MB,仍然会申请失败。
-
而链表恰恰相反,它并不需要一块连续的内存空间,它通过“指针”将一组零散的内存块 串联起来使用,所以如果我们申请的是 100MB 大小的链表,根本不会有问题。
2 链表分类
2.1 单链表
将所有的结点串起来,每个链表的结点除了存储数据之外,还需要记录链上的下一个结点的地址。如图所示,我们把这个记录下个结点地址的指针叫作后继指针 next 。

- 头结点 & 尾结点
- 我们习惯性地把第一个结点叫作头结点 ,把最后一个结点叫作尾结点 ;
- 头结点用来记录链表的基地址,有了它,我们就可以遍历得到整条链表;
- 尾结点特殊的地方是:指针不是指向下一个结点,而是指向一个空地址 NULL,表示这是链表上的最后一个结点;
- 哨兵节点:为了操作的便利,有时会将头结点设置为一个存储数据为null的节点;
2.2 循环链表
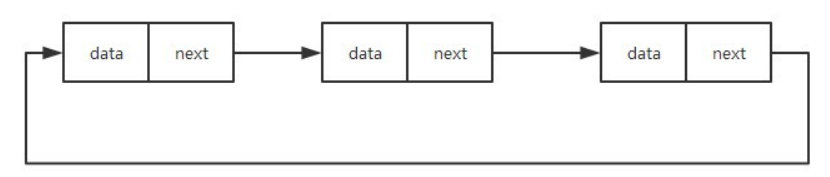
- 循环链表的尾结点指针是指向链表的头结点。它像一个环一样首尾相连,所以叫作“循环”链表
2.3 双向链表
-
双向链表需要额外的两个空间来存储后继结点 和前驱结点 的地址 。所以,如果存储同样多的数据,双向链表要比单链表占用更多的内存空间。虽然两个指针比较浪费存储空间,但可以支持双向遍历,这样也带来了双向链表操作的灵活性。
-
从结构上来看,双向链表可以支持 O(1) 时间复杂度的情况下找到前驱结点,正是这样的特点,也使双向链表在某些情况下的插入、删除等操作都要比单链表简单、高效。

2.4 双向循环链表

3 时间复杂度分析
3.1 插入和删除(理论)
-
在进行顺序表的插入、删除操作时,为了保持内存数据连续性,需要做大量的数据移动,所以时间复杂度是O(n) ;
-
在链表中插入或者删除一个数据,我们并不需要为了保持内存的连续性而移动结点,因为链表的存储空间本身就不是连续的。所以,在链表中插入和删除一个数据是非常快速的。我们只需要考虑相邻结点的指针改变,所以对应的时间复杂度是 O(1) ;
3.2 插入和删除(实际)
-
对链表进行“插入”或“删除”操作时,都需要从链表的头结点开始,依次找到待操作节点的前一个节点位置,然后再对链表进行“插入”或“删除”操作;
-
尽管对链表“插入”或“删除”一个节点的时间复杂度为O(1),但是每次都需要提前遍历待“插入”或“删除”节点的前一个位置,故遍历的时间复杂度为O(n),所以,对于任意一次的“插入”或“删除”操作都需要O(n);
-
插入操作:向第3个节点(下标为2)插入新节点,需要找到待插入节点的前一个节点位置,即第2个节点(下标为1)
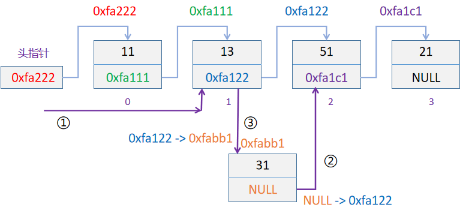

- 删除操作:删除第3个节点(下标为2),需要找到待插入节点的前一个节点位置,即第2个节点(下标为1)
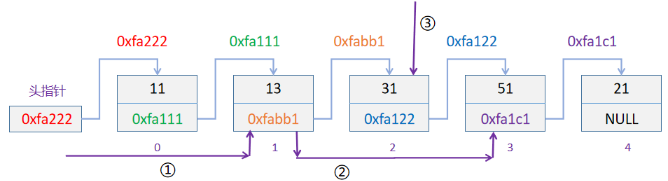
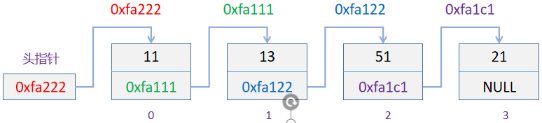
3.3 链表VS顺序表
- 时间复杂度考虑
| 链表 | 顺序表 | |
|---|---|---|
| 插入、删除 | O(1) | O(n) |
| 随机访问 | O(n) | O(1) |
- 动态扩容(重点)
- 链表天然地支持动态扩容,不受内存空间的限制;然而顺序表在内存空间不足时,会自动扩容,但是可能存在过多的闲置内存;
- cpu缓存预读
- 顺序表简单易用,在实现上使用的是连续的内存空间,可以借助 CPU 的缓存机制,预读顺序表中的数据,所以访问效率更高;
- 链表在内存中并不是连续存储,所以对 CPU 缓存不友好,没办法有效预读;
- 内存利用率
- 一般情况下,链表可以动态扩容,所以比一般数组内存利用率高。但若数组在已知要存储元素多少的情况下初始化,内存很少会被浪费,数组更优;
- 链表不适用于内存要求严苛的场景
- 链表中的每个结点都需要消耗额外的存储空间去存储一份指向下一个结点的指针,所以内存消耗会翻倍。但是对于比较大的Node,这点存指针的内存可以忽略;
- 对链表进行频繁的插入、删除操作,还会导致频繁的内存申请和释放,容易造成内存碎片;
4 代码演示
4.1 单链表
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define COLOR(a, b) "\033[" #b "m" a "\033[0m"
#define GREEN(a) COLOR(a, 32)
typedef struct Node {
int data;
struct Node *next; // 后继指针
} Node;
typedef struct List {
Node head; // 链表的虚拟头节点
int length; // 链表的节点个数
} List;
// 声明
Node *getNewNode(int);
List *init_list();
void clear_node(Node *);
void clear(List *);
int insert(List *, int, int);
int erase(List *, int);
void reverse(List *); // 链表翻转(原地翻转)
void reverse_first(List *, List *); // 链表翻转(头插法,需要开辟新的空间)
void output(List *);
int main() {
srand(time(0));
List *l = init_list();
#define MAX_OP 20
for (int i = 0; i < MAX_OP; i++) {
int val = rand() % 100;
int ind = rand() % (l->length + 3) - 1;
int op = rand() % 4;
switch (op) {
case 0: {
printf(GREEN("reverse the list!\n"));
// 使用头插法测试链表翻转时,需要开辟新的空间
List *nl = init_list();
reverse_first(l, nl), output(nl), clear(nl);
reverse(l);
} break;
case 1:
case 2: {
printf("insert %d at %d to List = %d\n", val, ind, insert(l, ind, val));
} break;
case 3: {
printf("erase an item at %d from List = %d\n", ind, erase(l, ind));
} break;
}
output(l), printf("\n");
}
#undef MAX_OP
clear(l);
return 0;
}
// 初始化一个节点
Node *getNewNode(int val) {
Node *node = (Node *)malloc(sizeof(Node));
node->data = val;
node->next = NULL;
return node;
}
// 初始化链表
List *init_list() {
List *l = (List *)malloc(sizeof(List));
l->head.next = NULL;
l->length = 0;
return l;
}
// 向链表l的第ind位置插入值val
int insert(List *l, int ind, int val) {
if (l == NULL) return 0;
if (ind < 0 || ind > l->length) return 0;
Node *p = &(l->head), *node = getNewNode(val);
while (ind--) p = p->next; // 移动到待插入节点的前一个节点位置
node->next = p->next; // 指向待插入节点的下一个节点
p->next = node; // 指向 待插入节点
l->length += 1;
return 1;
}
// 删除链表l中ind位置的元素
int erase(List *l, int ind) {
if (l == NULL) return 0;
if (ind < 0 || ind >= l->length) return 0;
Node *p = &(l->head), *q;
while (ind--) p = p->next; // 移动到待删除节点的前一个节点位置
q = p->next; // 待删除的节点
p->next = q->next; // 指向待删除节点的下一个节点位置
clear_node(q);
l->length -= 1;
return 1;
}
// 节点销毁
void clear_node(Node *node) {
if (node == NULL) return ;
free(node);
return ;
}
// 整个链表的销毁
void clear(List *l) {
if (l == NULL) return ;
Node *p = l->head.next, *q;
while (p != NULL) {
q = p->next;
clear_node(p);
p = q;
}
free(l);
return ;
}
// 链表的翻转(原地翻转,时间复杂度O(1))
void reverse(List *l) {
if (l == NULL) return ;
Node *p = l->head.next, *q;
l->head.next = NULL;
while (p != NULL) {
q = p->next;
p->next = l->head.next;
l->head.next = p;
p = q;
}
return ;
}
// 链表的翻转(头插法,需要重新开辟一块与待翻转链表同大小的空间)
void reverse_first(List *l, List *nl) {
if (l == NULL && nl == NULL) return ;
for (Node *p = l->head.next; p != NULL; p = p->next) {
insert(nl, 0, p->data);
}
return ;
}
void output(List *l) {
if (l == NULL) return ;
printf("list(%d) : ", l->length);
for (Node *p = l->head.next; p != NULL; p = p->next) {
printf("%d->", p->data);
}
printf("NULL\n");
return ;
}
4.2 双向链表
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
typedef struct Node {
int data;
struct Node *next, *pre;
} Node;
typedef struct DList {
Node head;
int length;
} DList;
Node *getNewNode(int val) {
Node *p = (Node *)malloc(sizeof(Node));
p->data = val;
p->next = NULL;
p->pre = NULL;
return p;
}
DList *init_list() {
DList *l = (DList *)malloc(sizeof(DList));
l->head.next = NULL;
l->length = 0;
return l;
}
int insert(DList *l, int ind, int val) {
if (l == NULL) return 0;
if (ind < 0 || ind > l->length) return 0;
Node *p = &(l->head), *node = getNewNode(val);
while (ind--) p = p->next;
node->next = p->next;
p->next = node;
node->pre = p;
if (node->next != NULL) node->next->pre = node;
l->length += 1;
return 1;
}
int erase(DList *l, int ind) {
if (l == NULL) return 0;
if (ind < 0 || ind >= l->length) return 0;
Node *p = &(l->head), *q;
while (ind--) p = p->next;
q = p->next;
p->next = q->next;
if (q->next != NULL) q->next->pre = p;
free(q);
l->length -= 1;
return 1;
}
void clear(DList *l) {
if (l == NULL) return ;
Node *p = l->head.next, *q;
while (p != NULL) {
q = p->next;
free(p);
p = q;
}
free(l);
return ;
}
void l_output(DList *l) {
if (l == NULL) return ;
printf("l_output(%d) : ", l->length);
for (Node *p = l->head.next; p; p = p->next) {
printf("%d->", p->data);
}
printf("NULL\n");
return ;
}
void r_output(DList *l) {
if (l == NULL) return ;
printf("r_output(%d) : ", l->length);
int ind = l->length;
Node *p = &(l->head);
while (ind--) p = p->next; // 将指针移动到链表末尾
for (; p != &(l->head); p = p->pre) {
printf("%d->", p->data);
}
printf("head\n");
return ;
}
int main() {
srand(time(0));
#define MAX_OP 20
DList *l = init_list();
for (int i = 0; i < MAX_OP; i++) {
int op, val, ind;
op = rand() % 4;
ind = rand() % (l->length + 3) - 1;
val = rand() % 100;
switch (op) {
case 0:
case 1:
case 2: {
printf("insert %d at %d to list = %d\n", val, ind, insert(l, ind, val));
break;
}
case 3: {
printf("erase a item at %d from list = %d\n", ind, erase(l, ind));
break;
}
}
l_output(l);
r_output(l), printf("\n");
}
#undef MAX_OP
clear(l);
return 0;
}
参考链接:https://blog.csdn.net/weixin_43935927/article/details/108710424

