1.1 例子：多项式曲线拟合

1.1 例子：多项式曲线拟合

问题描述

　　利用函数sin(2πx)产生一个带有随机噪声的训练集。训练集包括由x的N次观测：x = (x₁, ...,x_N)^T和对应的t的观测值t = (t₁,...,t_N)^T。利用该训练集拟合一个多项式曲线函数预测输入变量的新值x的目标变量的值t。

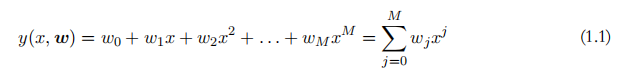
误差函数

　　对于公式1.1，要想使得对于输入x得到y(x, w) = t，需要调整多项式函数的系数值w。调整方法为最小化误差函数，即使得预测输出y(x, w) 与目标输出t之间的差异尽可能的小。这里采用的误差函数为常用的平方和误差：

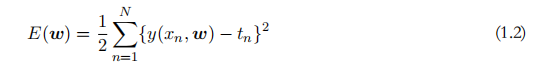
多项式拟合

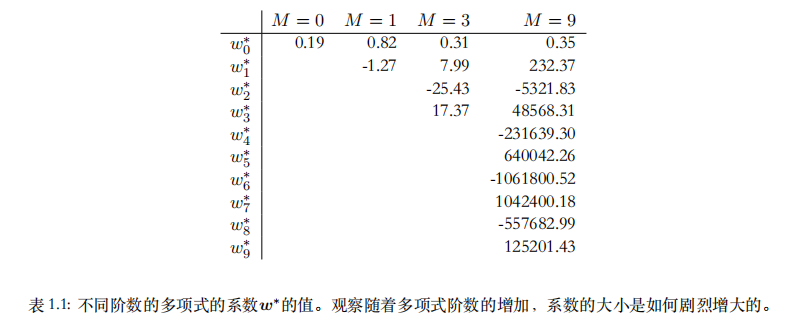
　　图1.4展示了多项式阶数M分别为0,1,3,9时多项式函数对训练集的拟合效果：

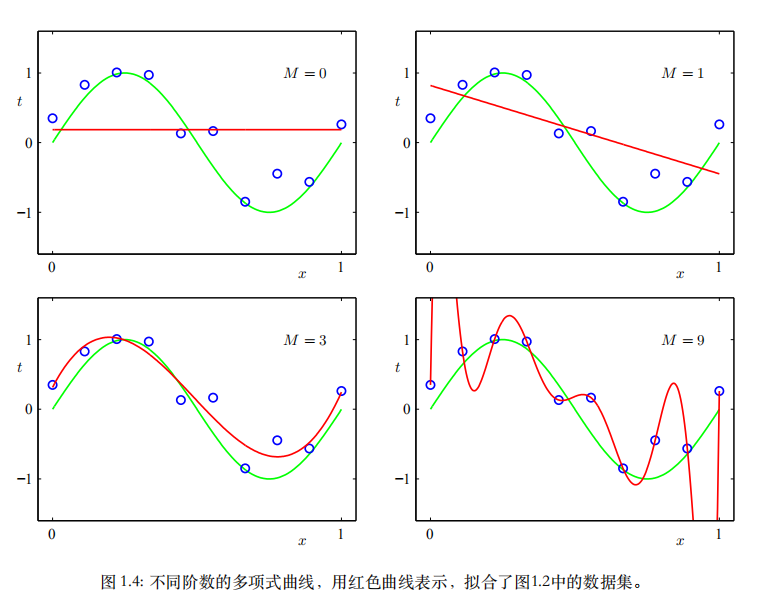
　　分析：M=0,1时，多项式函数表达能力较差，难以代表sin(2πx)函数；当M=9时，多项式函数完美拟合训练集中的每个点，但曲线震荡，对于新的满足sin(2πx)函数的点表达能力差，即出现过拟合现象；M=3时的多项式函数对sin(2πx)函数拟合效果相对较好。

 

 正则化

 　　当训练集数据增加时，能一定程度上缓解过拟合，另一种常用的控制过拟合的方法是正则化。这种技术涉及到给误差函数(1.2)增加⼀个惩罚项，使得系数不会达到很⼤的值，减小拟合函数的震荡。这里的惩罚项为系数w的平方和，则正则化的误差函数如下：

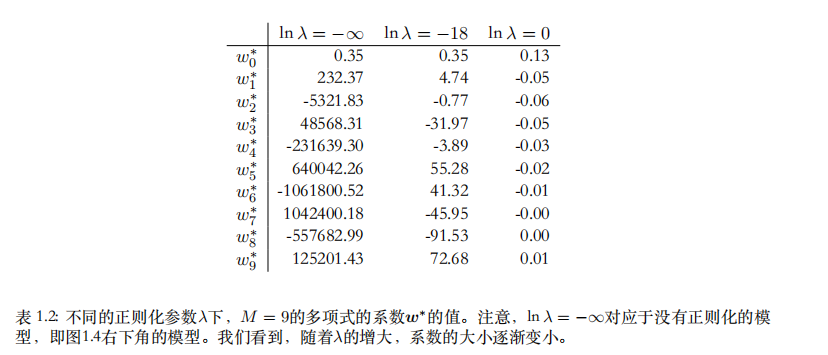
　　下图展示了M=9的多项式函数在添加了正则项后的拟合效果：

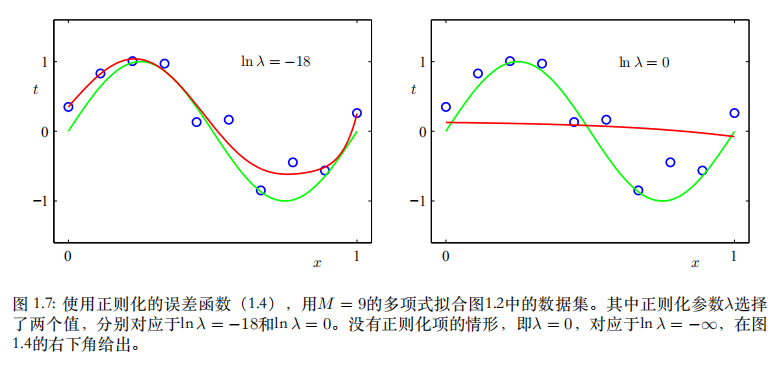
　　另外，如下图，M=9时，正则化多项式函数权重值的浮动显著小于未正则化的权重：

小结

 以多项式拟合为例。训练过程可以描述为：利用一组已知输入及对应输出的训练集合，通过最小化误差函数，调整函数模型中的权重参数，使得模型输出与目标输出尽可能相似。在这个过程中，由于训练数据过少、噪声干扰等问题，可能会使得模型泛化能力差，一种常用的解决方法为才误差函数中增加惩罚项，防止系数被过分调参。