算法(Algorithm)是指用来操作数据、解决程序问题的一组方法。对于同一个问题,使用不同的算法,也许最终得到的结果是一样的,比如排序就有经典排序和几种奇葩排序,虽然结果相同,但在过程中消耗的资源和时间却会有很大的区别,比如快速排序与猴子排序:)。
那么我们应该如何去衡量不同算法之间的优劣呢?
主要还是从算法所占用的「时间」和「空间」两个维度去考量。
-
时间维度:是指执行当前算法所消耗的时间,我们通常用「时间复杂度」来描述。
-
空间维度:是指执行当前算法需要占用多少内存空间,我们通常用「空间复杂度」来描述。
我们假设计算机运行一行基础代码需要执行一次运算。
1 int aFunc(void) { 2 printf("Hello, World!\n"); // 需要执行 1 次 3 return 0; // 需要执行 1 次 4 }
那么上面这个方法需要执行 2 次运算
1 int aFunc(int n) { 2 for(int i = 0; i<n; i++) { // 需要执行 (n + 1) 次 3 printf("Hello, World!\n"); // 需要执行 n 次 4 } 5 return 0; // 需要执行 1 次 6 }
这个方法需要 (n + 1 + n + 1) = 2n + 2 次运算。
我们把 算法需要执行的运算次数 用 输入大小n 的函数 表示,即 T(n) 。
此时为了 估算算法需要的运行时间 和 简化算法分析,我们引入时间复杂度的概念。
定义:存在常数 c 和函数 f(N),使得当 N >= c 时 T(N) <= f(N),表示为 T(n) = O(f(n)) 。
如图:
大O符号(Big O notation)是用于描述函数渐进行为的数学符号。更确切地说,它是用另一个(通常更简单的)函数来描述一个函数数量级(Orders of magnitude)的渐近上界。在数学中,它一般用来刻画被截断的无穷级数尤其是渐近级数的剩余项;在计算机科学中,它在分析算法复杂性的方面非常有用。
如图:
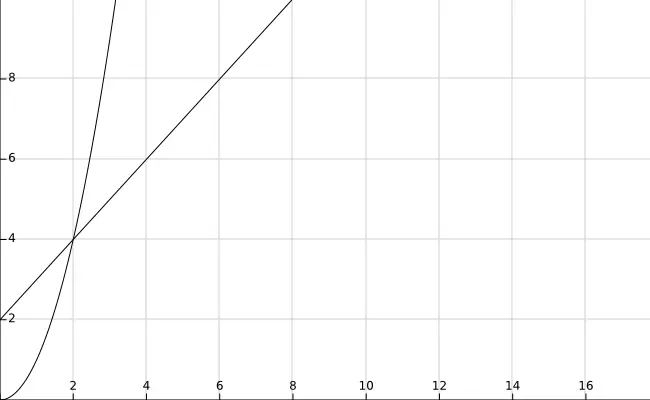
当 N >= 2 的时候,f(n) = n^2 总是大于 T(n) = n + 2 的,于是我们说 f(n) 的增长速度是大于或者等于 T(n) 的,也说 f(n) 是 T(n) 的上界,可以表示为 T(n) = O(f(n))。
因为f(n) 的增长速度是大于或者等于 T(n) 的,即T(n) = O(f(n)),所以我们可以用 f(n) 的增长速度来度量 T(n) 的增长速度,所以我们说这个算法的时间复杂度是 O(f(n))。
算法的时间复杂度,用来度量算法的运行时间,记作: T(n) = O(f(n))。它表示随着 输入大小n 的增大,算法执行需要的时间的增长速度可以用 f(n) 来描述。
那么当我们拿到算法的执行次数函数 T(n) 之后怎么得到算法的时间复杂度呢?
- 我们知道常数项对函数的增长速度影响并不大,所以当 T(n) = c,c 为一个常数的时候,我们说这个算法的时间复杂度为 O(1);如果 T(n) 不等于一个常数项时,直接将常数项省略。
1 比如 2 第一个 Hello, World 的例子中 T(n) = 2,所以我们说那个函数(算法)的时间复杂度为 O(1)。 3 T(n) = n + 29,此时时间复杂度为 O(n)。
- 我们知道高次项对于函数的增长速度的影响是最大的。n^3 的增长速度是远超 n^2 的,同时 n^2 的增长速度是远超 n 的。 同时因为要求的精度不高,所以我们直接忽略低此项。
1 比如 2 T(n) = n^3 + n^2 + 29,此时时间复杂度为 O(n^3)。
- 因为函数的阶数对函数的增长速度的影响是最显著的,所以我们忽略与最高阶相乘的常数。
1 比如 2 T(n) = 3n^3,此时时间复杂度为 O(n^3)。
综合起来:如果一个算法的执行次数是 T(n),那么只保留最高次项,同时忽略最高项的系数后得到函数 f(n),此时算法的时间复杂度就是 O(f(n))。为了方便描述,下文称此为 大O推导法。
由此可见,由执行次数 T(n) 得到时间复杂度并不困难,很多时候困难的是从算法通过分析和数学运算得到 T(n)。对此,提供下列四个便利的法则,这些法则都是可以简单推导出来的,总结出来以便提高效率。
- 对于一个循环,假设循环体的时间复杂度为 O(n),循环次数为 m,则这个
循环的时间复杂度为 O(n×m)。
1 void aFunc(int n) { 2 for(int i = 0; i < n; i++) { // 循环次数为 n 3 printf("Hello, World!\n"); // 循环体时间复杂度为 O(1) 4 } 5 }
此时时间复杂度为 O(n × 1),即 O(n)。
- 对于多个循环,假设循环体的时间复杂度为 O(n),各个循环的循环次数分别是a, b, c...,则这个循环的时间复杂度为 O(n×a×b×c...)。分析的时候应该由里向外分析这些循环。
1 void aFunc(int n) { 2 for(int i = 0; i < n; i++) { // 循环次数为 n 3 for(int j = 0; j < n; j++) { // 循环次数为 n 4 printf("Hello, World!\n"); // 循环体时间复杂度为 O(1) 5 } 6 } 7 }
此时时间复杂度为 O(n × n × 1),即 O(n^2)。
- 对于顺序执行的语句或者算法,总的时间复杂度等于其中最大的时间复杂度。
1 void aFunc(int n) { 2 // 第一部分时间复杂度为 O(n^2) 3 for(int i = 0; i < n; i++) { 4 for(int j = 0; j < n; j++) { 5 printf("Hello, World!\n"); 6 } 7 } 8 // 第二部分时间复杂度为 O(n) 9 for(int j = 0; j < n; j++) { 10 printf("Hello, World!\n"); 11 } 12 }
此时时间复杂度为 max(O(n^2), O(n)),即 O(n^2)。
- 对于条件判断语句,总的时间复杂度等于其中 时间复杂度最大的路径 的时间复杂度。
1 void aFunc(int n) { 2 if (n >= 0) { 3 // 第一条路径时间复杂度为 O(n^2) 4 for(int i = 0; i < n; i++) { 5 for(int j = 0; j < n; j++) { 6 printf("输入数据大于等于零\n"); 7 } 8 } 9 } else { 10 // 第二条路径时间复杂度为 O(n) 11 for(int j = 0; j < n; j++) { 12 printf("输入数据小于零\n"); 13 } 14 } 15 }
此时时间复杂度为 max(O(n^2), O(n)),即 O(n^2)。
时间复杂度分析的基本策略是:从内向外分析,从最深层开始分析。如果遇到函数调用,要深入函数进行分析。
对数是对求幂的逆运算,正如除法是乘法的倒数,反之亦然。
-
特别地,我们称以10为底的对数叫做常用对数(common logarithm),并记为lg。
-
称以无理数e(e=2.71828...)为底的对数称为自然对数(natural logarithm),并记为ln。
-
零没有对数。
若算法的T(n) =O(logn),则称其具有对数时间。由于计算机使用二进制的记数系统,对数常常以2为底(即log2n,有时写作lgn)。然而,由对数的换底公式,logan和logbn只有一个常数因子不同,这个因子在大O记法中被丢弃。因此记作O(logn),而不论对数的底是多少,是对数时间算法的标准记法。
我们来练习一下
一. 基础题
求该方法的时间复杂度
1 void aFunc(int n) { 2 for (int i = 0; i < n; i++) { 3 for (int j = i; j < n; j++) { 4 printf("Hello World\n"); 5 } 6 } 7 }
参考答案:
当 i = 0 时,内循环执行 n 次运算,当 i = 1 时,内循环执行 n - 1 次运算……当 i = n - 1 时,内循环执行 1 次运算。
所以,执行次数 T(n) = n + (n - 1) + (n - 2)……+ 1 = n(n + 1) / 2 = n^2 / 2 + n / 2。
根据上文说的 大O推导法 可以知道,此时时间复杂度为 O(n^2)。
二. 进阶题
求该方法的时间复杂度
1 void aFunc(int n) { 2 for (int i = 2; i < n; i++) { 3 i *= 2; 4 printf("%i\n", i); 5 } 6 }
参考答案:
假设循环次数为 t,则循环条件满足 2^t < n。
可以得出,执行次数t = log(2)(n),即 T(n) = log(2)(n),可见时间复杂度为 O(log(2)(n)),即 O(log n)。
三. 再次进阶
求该方法的时间复杂度
1 long aFunc(int n) { 2 if (n <= 1) { 3 return 1; 4 } else { 5 return aFunc(n - 1) + aFunc(n - 2); 6 } 7 }
参考答案:
显然运行次数,T(0) = T(1) = 1,同时 T(n) = T(n - 1) + T(n - 2) + 1,这里的 1 是其中的加法算一次执行。
显然 T(n) = T(n - 1) + T(n - 2) 是一个斐波那契数列,通过归纳证明法可以证明,当 n >= 1 时 T(n) < (5/3)^n,同时当 n > 4 时 T(n) >= (3/2)^n。
所以该方法的时间复杂度可以表示为 O((5/3)^n),简化后为 O(2^n)。
可见这个方法所需的运行时间是以指数的速度增长的。
常见的时间复杂度量级:
-
常数阶O(1)
-
线性阶O(n)
-
平方阶O(n²)
-
对数阶O(logn)
-
线性对数阶O(nlogn)
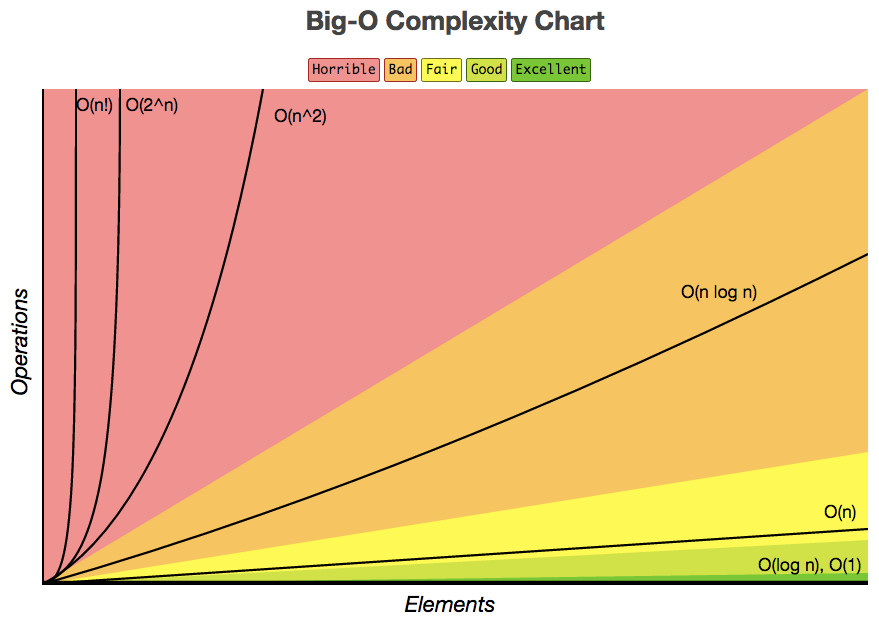
O(1):

无论代码执行了多少行,其他区域不会影响到操作,这个代码的时间复杂度都是O(1)
1 void swapTwoInts(int &a, int &b){ 2 int temp = a; 3 a = b; 4 b = temp; 5 }
O(n):
在下面这段代码,for循环里面的代码会执行 n 遍,因此它消耗的时间是随着 n 的变化而变化的,因此可以用O(n)来表示它的时间复杂度。
1 int sum ( int n ){ 2 int ret = 0; 3 for ( int i = 0 ; i <= n ; i ++){ 4 ret += i; 5 } 6 return ret; 7 }
特别一提的是 c * O(n) 中的 c 可能小于 1 ,比如下面这段代码:
1 void reverse ( string &s ) { 2 int n = s.size(); 3 for (int i = 0 ; i < n/2 ; i++){ 4 swap ( s[i] , s[n-1-i]); 5 } 6 }
O(n²):

当存在双重循环的时候,即把 O(n) 的代码再嵌套循环一遍,它的时间复杂度就是 O(n²) 了。
1 void selectionSort(int arr[],int n){ 2 for(int i = 0; i < n ; i++){ 3 int minIndex = i; 4 for (int j = i + 1; j < n ; j++ ) 5 if (arr[j] < arr[minIndex]) 6 minIndex = j; 7 8 swap ( arr[i], arr[minIndex]); 9 } 10 }
这里简单的推导一下
- 当 i = 0 时,第二重循环需要运行 (n - 1) 次
- 当 i = 1 时,第二重循环需要运行 (n - 2) 次
- 。。。。。。
不难得到公式:
(n - 1) + (n - 2) + (n - 3) + ... + 0
= (0 + n - 1) * n / 2
= O (n ^2)
当然并不是所有的双重循环都是 O(n²),比如下面这段输出 30n 次 Hello,world:)的代码。
1 void printInformation (int n ){ 2 for (int i = 1 ; i <= n ; i++) 3 for (int j = 1 ; j <= 30 ; j ++) 4 cout<< "Hello,world:)"<< endl; 5 }
O(logn):
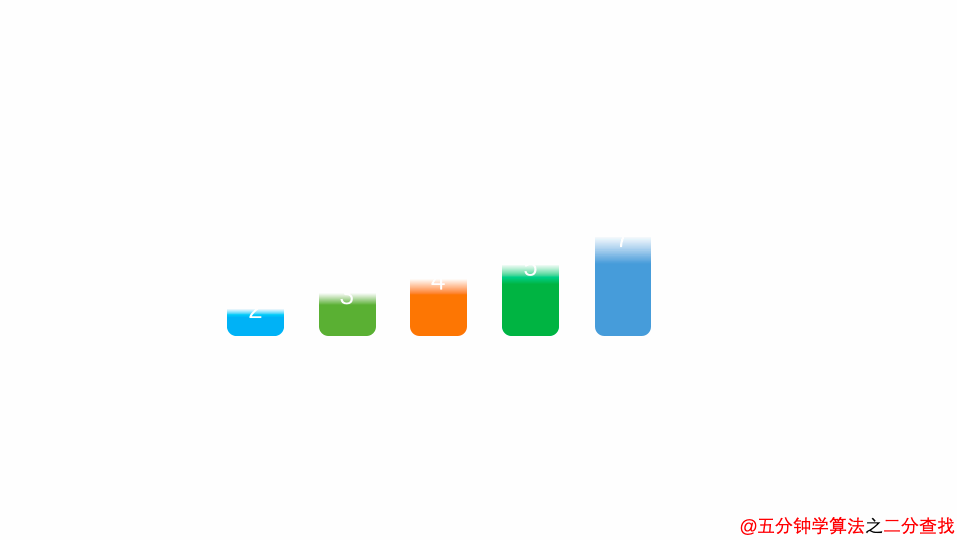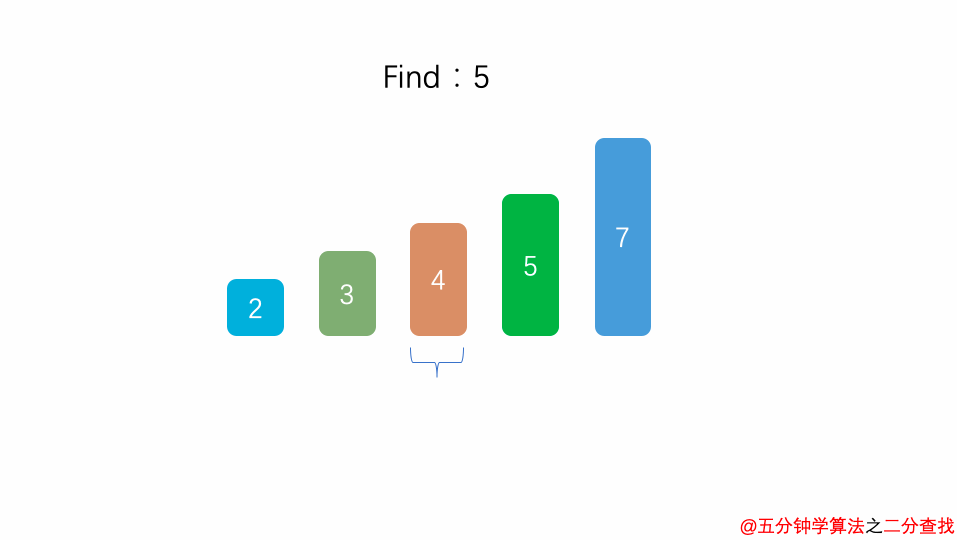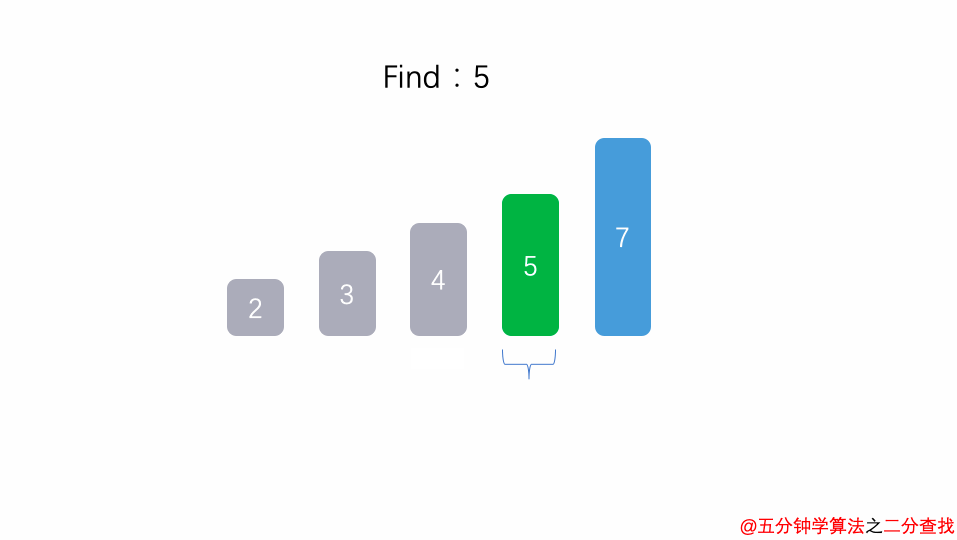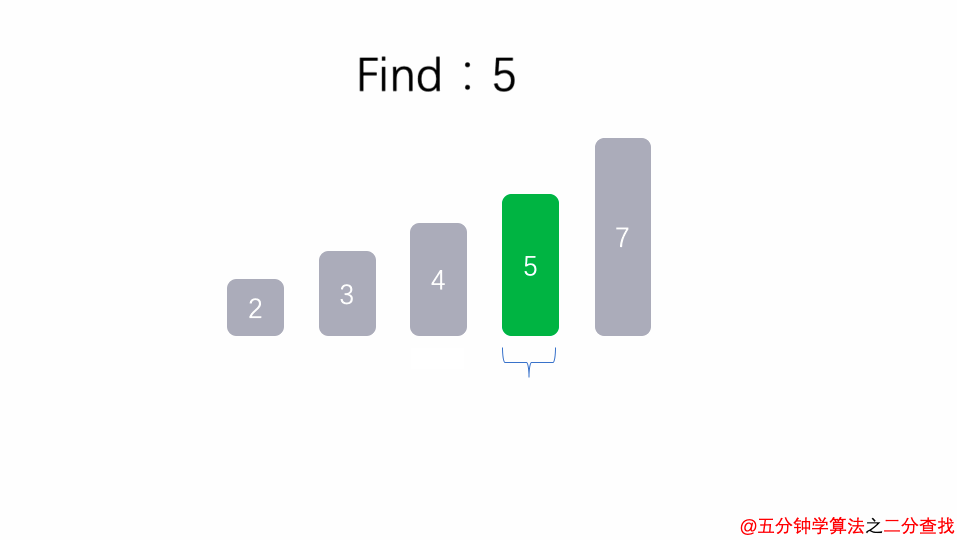
1 int binarySearch( int arr[], int n , int target){ 2 int l = 0, r = n - 1; 3 while ( l <= r) { 4 int mid = l + (r - l) / 2; 5 if (arr[mid] == target) return mid; 6 if (arr[mid] > target ) r = mid - 1; 7 else l = mid + 1; 8 } 9 return -1; 10 }
在二分查找法的代码中,通过while循环,成 2 倍数的缩减搜索范围,也就是说需要经过 log2^n 次即可跳出循环。
同样的还有下面两段代码也是 O(logn) 级别的时间复杂度。
1 // 整形转成字符串 2 string intToString ( int num ){ 3 string s = ""; 4 // n 经过几次“除以10”的操作后,等于0 5 while (num ){ 6 s += '0' + num%10; 7 num /= 10; 8 } 9 reverse(s) 10 return s; 11 } 12 void hello (int n ) { 13 // n 除以几次 2 到 1 14 for ( int sz = 1; sz < n ; sz += sz) 15 for (int i = 1; i < n; i++) 16 cout<< "Hello,五分钟学算法:)"<< endl; 17 }
O(nlogn):
将时间复杂度为O(logn)的代码循环N遍的话,那么它的时间复杂度就是 n * O(logn),也就是了O(nlogn)。
1 void hello (){ 2 for( m = 1 ; m < n ; m++){ 3 i = 1; 4 while( i < n ){ 5 i = i * 2; 6 } 7 } 8 }
不常见的时间复杂度
下面来分析一波另外几种复杂度: 递归算法的时间复杂度(recursive algorithm time complexity),最好情况时间复杂度(best case time complexity)、最坏情况时间复杂度(worst case time complexity)、平均时间复杂度(average case time complexity)和均摊时间复杂度(amortized time complexity)。
递归算法的时间复杂度
如果递归函数中,只进行一次递归调用,递归深度为depth;
在每个递归的函数中,时间复杂度为T;
则总体的时间复杂度为O(T * depth)。
在前面的学习中,归并排序 与 快速排序 都带有递归的思想,并且时间复杂度都是O(nlogn) ,但并不是有递归的函数就一定是 O(nlogn) 级别的。从以下两种情况进行分析。
① 递归中进行一次递归调用的复杂度分析
二分查找法
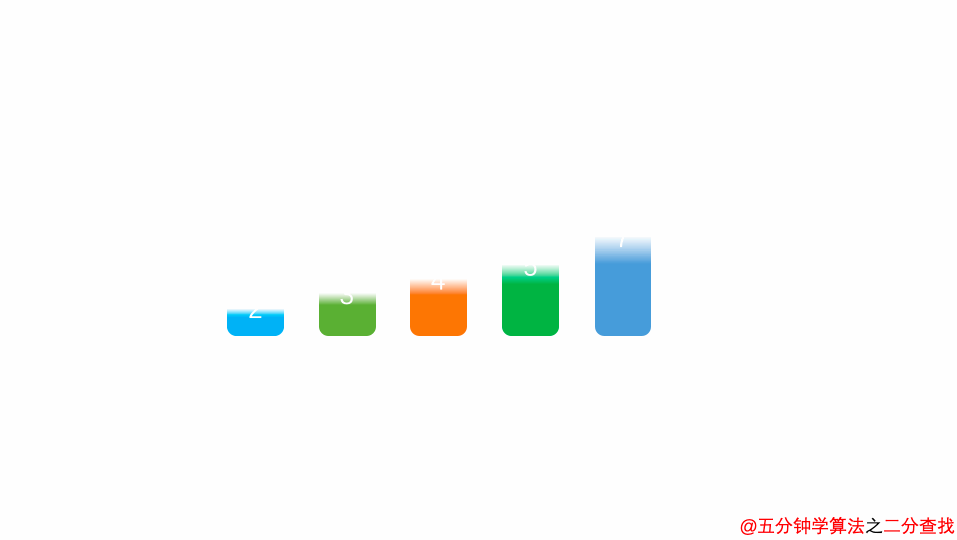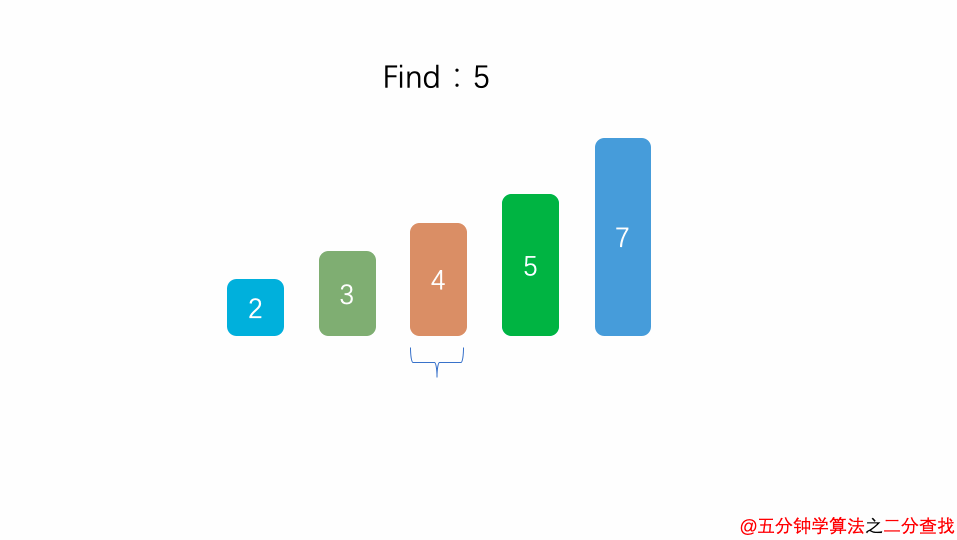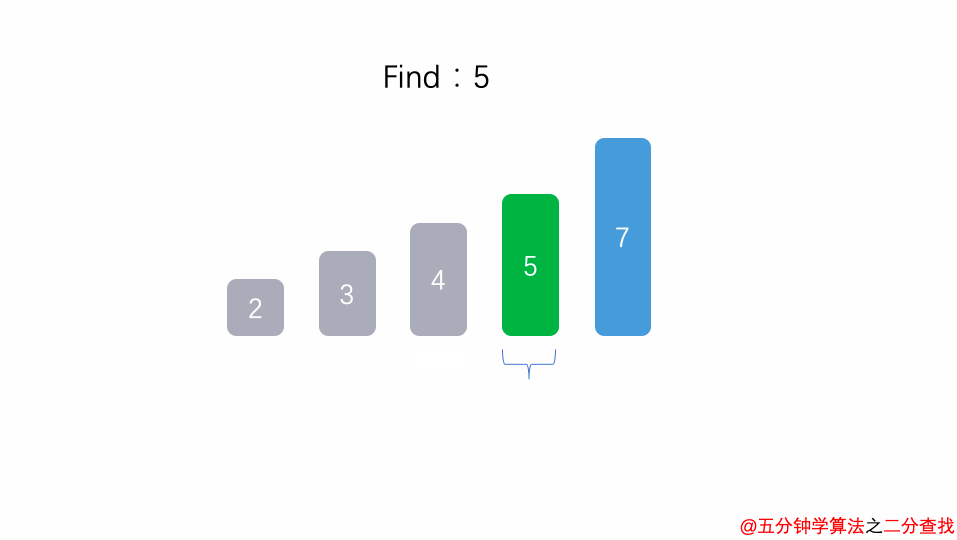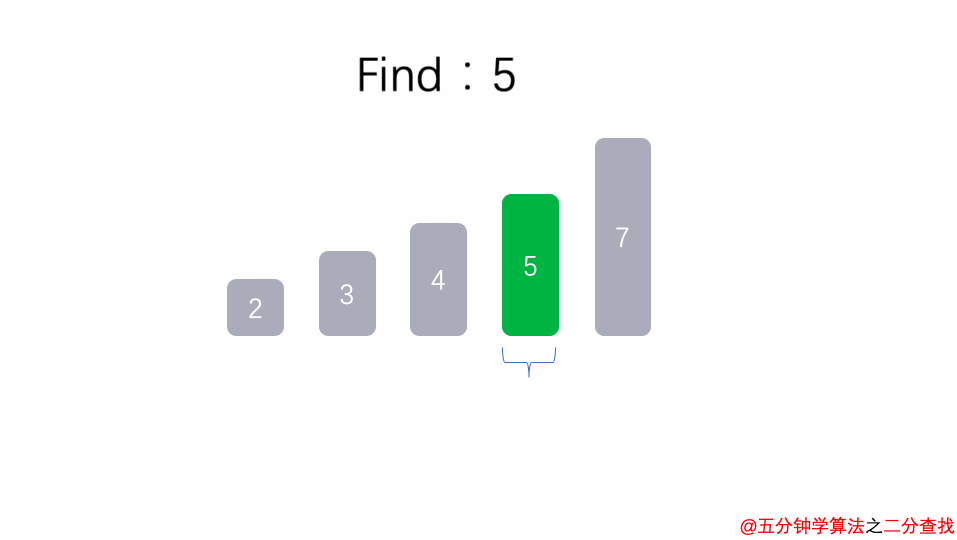
1 int binarySearch(int arr[], int l, int r, int target){ 2 if( l > r ) return -1; 3 4 int mid = l + (r-l)/2; 5 if( arr[mid] == target ) return mid; 6 else if( arr[mid] > target ) 7 return binarySearch(arr, l, mid-1, target); // 左边 8 else 9 return binarySearch(arr, mid+1, r, target); // 右边 10 }
比如在这段二分查找法的代码中,每次在 [ l , r ] 范围中去查找目标的位置,如果中间的元素 arr[mid] 不是 target,那么判断 arr[mid]是比 target 大 还是 小 ,进而再次调用 binarySearch这个函数。
在这个递归函数中,每一次没有找到target时,要么调用 左边 的 binarySearch函数,要么调用 右边 的 binarySearch函数。也就是说在此次递归中,最多调用了一次递归调用而已。根据数学知识,需要log2n次才能递归到底。因此,二分查找法的时间复杂度为 O(logn)。
求和:

1 int sum (int n) { 2 if (n == 0) return 0; 3 return n + sum( n - 1 ) 4 }
在这段代码中比较容易理解递归深度随输入 n 的增加而线性递增,因此时间复杂度为 O (n)。
求幂:

1 //递归深度:logn 2 //时间复杂度:O(logn) 3 double pow( double x, int n){ 4 if (n == 0) return 1.0; 5 6 double t = pow(x,n/2); 7 if (n %2) return x*t*t; 8 return t * t; 9 }
递归深度为 logn,因为是求需要除以 2 多少次才能到底。
② 递归中进行多次递归调用的复杂度分析
递归算法中比较难计算的是多次递归调用。
先看下面这段代码,有两次递归调用。
1 // O(2^n) 指数级别的数量级,后续动态规划的优化点 2 int f(int n){ 3 if (n == 0) return 1; 4 return f(n-1) + f(n - 1); 5 }

递归树中节点数就是代码计算的调用次数。
比如 当 n = 3 时,调用次数计算公式为
1 + 2 + 4 + 8 = 15
一般的,调用次数计算公式为
20 + 21 + 22 + …… + 2n
= 2(n+1) - 1
= O(2n)

与之有所类似的是 归并排序 的递归树,区别点在于
- 上述例子中树的深度为
n,而 归并排序 的递归树深度为logn。
- 上述例子中树的深度为
- 上述例子中每次处理的数据规模是一样的,而在 归并排序 中每个节点处理的数据规模是逐渐缩小的
因此,在如 归并排序 等排序算法中,每一层处理的数据量为 O(n) 级别,同时有 logn 层,时间复杂度便是 O(nlogn)。
最好、最坏情况时间复杂度

最好、最坏情况时间复杂度指的是特殊情况下的时间复杂度。
动图表明的是在数组 array 中寻找变量 x 第一次出现的位置,若没有找到,则返回 -1;否则返回位置下标。
1 int find(int[] array, int n, int x) { 2 for ( int i = 0 ; i < n; i++) { 3 if (array[i] == x) { 4 return i; 5 break; 6 } 7 } 8 return -1; 9 }
在这里当数组中第一个元素就是要找的 x 时,时间复杂度是 O(1);而当最后一个元素才是 x 时,时间复杂度则是 O(n)。
最好情况时间复杂度就是在最理想情况下执行代码的时间复杂度,它的时间是最短的;最坏情况时间复杂度就是在最糟糕情况下执行代码的时间复杂度,它的时间是最长的。
平均情况时间复杂度
最好、最坏时间复杂度反应的是极端条件下的复杂度,发生的概率不大,不能代表平均水平。那么为了更好的表示平均情况下的算法复杂度,就需要引入平均时间复杂度。
平均情况时间复杂度可用代码在所有可能情况下执行次数的加权平均值表示。
还是以 find 函数为例,从概率的角度看, x 在数组中每一个位置的可能性是相同的,为 1 / n。那么,那么平均情况时间复杂度就可以用下面的方式计算:
((1 + 2 + … + n) / n + n) / 2 = (3n + 1) / 4
find 函数的平均时间复杂度为 O(n)。
均摊复杂度分析
我们通过一个动态数组的 push_back 操作来理解 均摊复杂度。

1 template <typename T> 2 class MyVector{ 3 private: 4 T* data; 5 int size; // 存储数组中的元素个数 6 int capacity; // 存储数组中可以容纳的最大的元素个数 7 // 复杂度为 O(n) 8 void resize(int newCapacity){ 9 T *newData = new T[newCapacity]; 10 for( int i = 0 ; i < size ; i ++ ){ 11 newData[i] = data[i]; 12 } 13 data = newData; 14 capacity = newCapacity; 15 } 16 public: 17 MyVector(){ 18 data = new T[100]; 19 size = 0; 20 capacity = 100; 21 } 22 // 平均复杂度为 O(1) 23 void push_back(T e){ 24 if(size == capacity) 25 resize(2 * capacity); 26 data[size++] = e; 27 } 28 // 平均复杂度为 O(1) 29 T pop_back(){ 30 size --; 31 return data[size]; 32 } 33 34 };
push_back实现的功能是往数组的末尾增加一个元素,如果数组没有满,直接往后面插入元素;如果数组满了,即 size == capacity ,则将数组扩容一倍,然后再插入元素。
例如,数组长度为 n,则前 n 次调用 push_back 复杂度都为 O(1) 级别;在第 n + 1 次则需要先进行 n 次元素转移操作,然后再进行 1 次插入操作,复杂度为 O(n)。
因此,平均来看:对于容量为 n 的动态数组,前面添加元素需要消耗了 1 * n 的时间,扩容操作消耗 n 时间 ,
总共就是 2 * n 的时间,因此均摊时间复杂度为 O(2n / n) = O(2),也就是 O(1) 级别了。
可以得出一个比较有意思的结论:一个相对比较耗时的操作,如果能保证它不会每次都被触发,那么这个相对比较耗时的操作,它所相应的时间是可以分摊到其它的操作中来的。
空间复杂度
一个程序的空间复杂度是指运行完一个程序所需内存的大小。利用程序的空间复杂度,可以对程序的运行所需要的内存多少有个预先估计。一个程序执行时除了需要存储空间和存储本身所使用的指令、常数、变量和输入数据外,还需要一些对数据进行操作的工作单元和存储一些为现实计算所需信息的辅助空间。程序执行时所需存储空间包括以下两部分:
(1) 固定部分,这部分空间的大小与输入/输出的数据的个数多少、数值无关。主要包括指令空间(即代码空间)、数据空间(常量、简单变量)等所占的空间。这部分属于静态空间。
(2) 可变空间,这部分空间的主要包括动态分配的空间,以及递归栈所需的空间等。这部分的空间大小与算法有关。
一个算法所需的存储空间用f(n)表示。S(n)=O(f(n)),其中n为问题的规模,S(n)表示空间复杂度。
空间复杂度可以理解为除了原始序列大小的内存,在算法过程中用到的额外的存储空间。
以二叉查找树为例,举例说明二叉排序树的查找性能。
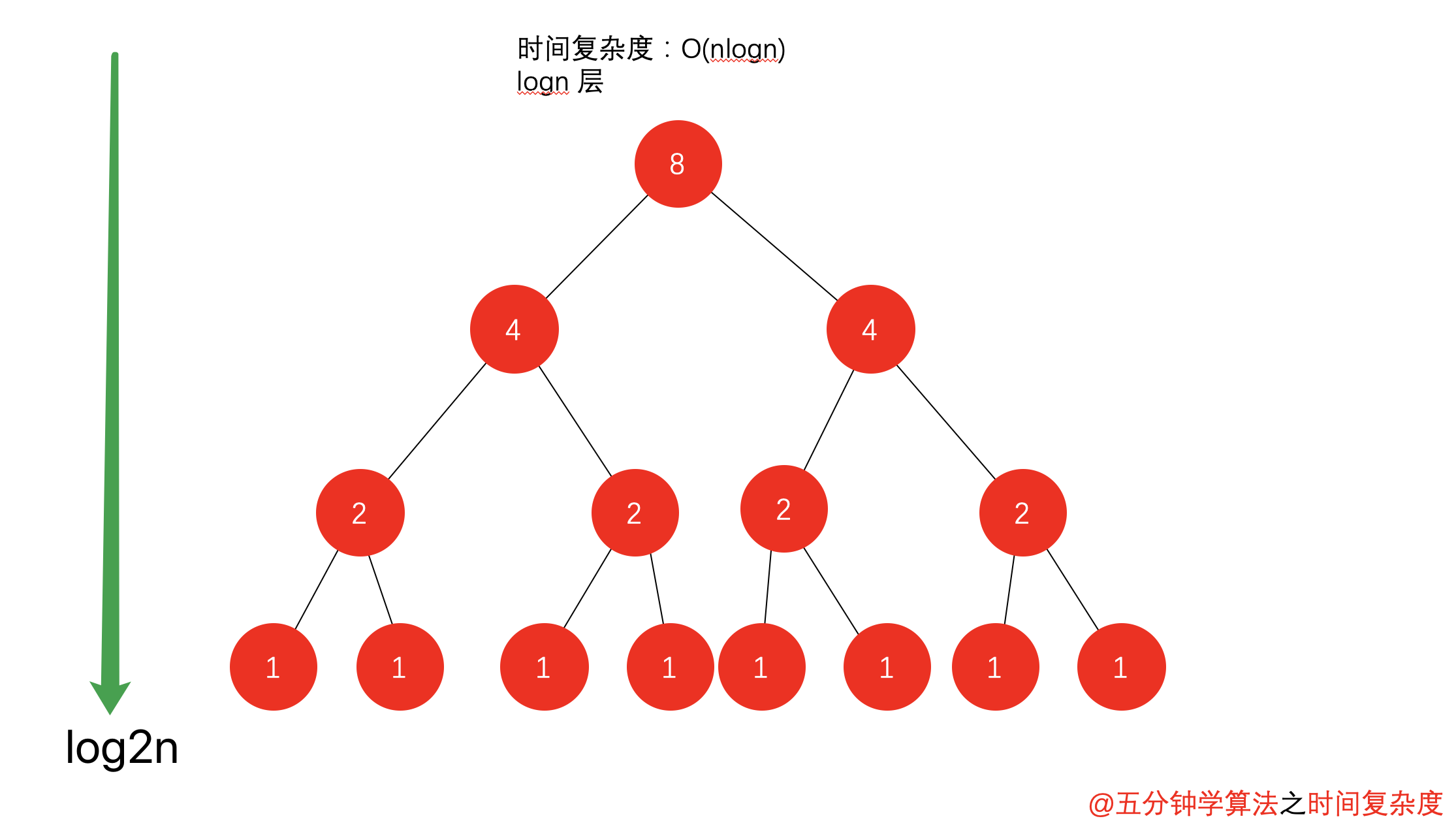
平衡二叉树
如果二叉树的是以红黑树等平衡二叉树实现的,则 n 个节点的二叉排序树的高度为 log2n+1 ,其查找效率为O(Log2n),近似于折半查找。
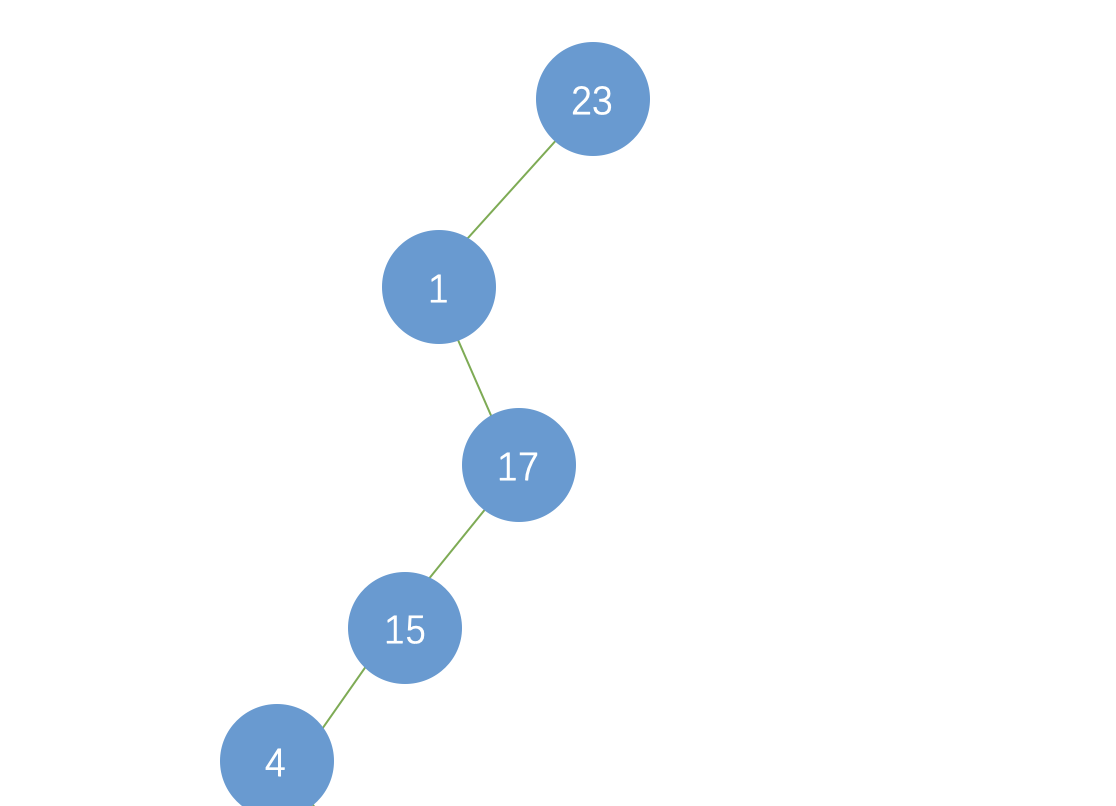
列表二叉树
如果二叉树退变为列表了,则 n 个节点的高度或者说是长度变为了n,查找效率为O(n),变成了顺序查找
一般二叉树
介于「列表二叉树」与「平衡二叉树」之间,查找性能也在O(Log2n)到O(n)之间。
总结:
对于一个算法,其时间复杂度和空间复杂度往往是相互影响的。
比如说,要判断某某年是不是闰年:
- 可以编写一个算法来计算,这也就意味着,每次给一个年份,都是要通过计算得到是否是闰年的结果。
- 还有另一个办法就是,事先建立一个有 5555 个元素的数组(年数比现实多就行),然后把所有的年份按下标的数字对应,如果是闰年,此数组项的值就是1,如果不是值为0。这样,所谓的判断某一年是否是闰年,就变成了查找这个数组的某一项的值是多少的问题。此时,我们的运算是最小化了,但是硬盘上或者内存中需要存储这 5555 个 0 和 1 。
这就是典型的使用空间换时间的概念。
当追求一个较好的时间复杂度时,可能会使空间复杂度的性能变差,即可能导致占用较多的存储空间;
反之,求一个较好的空间复杂度时,可能会使时间复杂度的性能变差,即可能导致占用较长的运行时间。
另外,算法的所有性能之间都存在着或多或少的相互影响。因此,当设计一个算法(特别是大型算法)时,要综合考虑算法的各项性能,算法的使用频率,算法处理的数据量的大小,算法描述语言的特性,算法运行的机器系统环境等各方面因素,才能够设计出比较好的算法。
参考:
0.https://mp.weixin.qq.com/s/1rYK3urLuun5WqnibJ2t3g
1.https://www.jianshu.com/p/f4cca5ce055a
2.https://cxyxiaowu.com/articles/2019/04/04/1554345342924.html
3.https://cxyxiaowu.com/articles/2019/04/04/1554345100970.html
4.https://cxyxiaowu.com/articles/2019/04/04/1554345130826.html
5.https://www.jianshu.com/p/89f4f0831d6c
6.https://www.cnblogs.com/gaochundong/p/complexity_of_algorithms.html
7.https://www.zhihu.com/question/21387264
8.https://blog.csdn.net/CrankZ/article/details/84726408



