定义 S4 泛型函数

在前面的例子中，我们可以看出 S4 比 S3 更正式，因为 S4 类有类的正式定义。同样，

S4 的泛型函数也更加正式。
在一个关于形状的例子中，我们定义了一系列具有继承关系的 S4 类，只是继承关系的层级
结构比较简单。首先，Shape 是处于根节点的类，Polygon 和 Circle 都继承自 Shape，而
Triangle 和Rectangle 继承自Polygon。这些形状的继承结构如图10-5 所示。

 

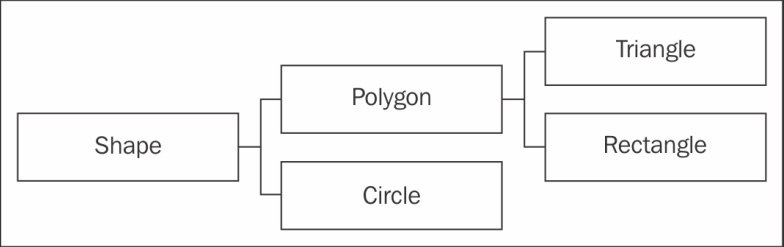
图 10-5
除了 Shape 类，其他每个类都有一些用于描述这个类必要的字段：
setClass("Shape")
setClass("Polygon",
representation(sides = "integer"),
contains = "Shape")
setClass("Triangle",
representation(a = "numeric", b = "numeric", c = "numeric"),
prototype(a = 1, b = 1, c = 1, sides = 3L),
contains = "Polygon")
setClass("Rectangle",
representation(a = "numeric", b = "numeric"),
prototype(a = 1, b = 1, sides = 4L),
contains = "Polygon")
setClass("Circle",
representation(r = "numeric"),
prototype(r = 1, sides = Inf),
contains = "Shape")
定义了这些类，我们就可以构建一个泛型函数来计算一个 Shape 对象的面积。为此，
我们需要调用 setGeneric( )创建一个新的泛型函数：area( )，并为 area( )提供
一个调用 standardGeneric("area")的函数来使这个新的泛型函数可用于 S4 方法分
派。参数 valueClass 是用来确保每种方法的返回值必须是 numeric 类：
setGeneric("area", function(object) {
standardGeneric("area")
}, valueClass = "numeric")
## [1] "area"
一旦构建了泛型函数，我们就可以为不同种类的形状实现不同的方法。对于 Triangle，
给定三角形的 3 个边长，使用海伦公式[Heron's formula（https://en.wikipedia.org/wiki/Heron's_
formula）]来计算它的面积：
setMethod("area", signature("Triangle"), function(object) {
a <- object@a
b <- object@b
c <- object@c
s <- (a + b + c) / 2
sqrt(s * (s -a) *(s -b) * (s -c))
})
## [1] "area"
对于 Rectangle 和 Circle，我们可以很容易地写出它们的面积公式：
setMethod("area", signature("Rectangle"), function(object) {
object@a *object@b
})
## [1] "area"
setMethod("area", signature("Circle"), function(object) {
pi *object@r ^2
})
## [1] "area"
现在，我们创建一个 Triangle 类的对象实例，并查看泛型函数 area( )是否会分
派正确的方法，然后返回正确的答案：
triangle <- new("Triangle", a = 3, b = 4, c = 5)
area(triangle)
## [1] 6
再创建一个 Circle 类对象实例，看看方法分派是否正常进行：
circle <- new("Circle", r = 3)
area(circle)
## [1] 28.27433
两个答案都是正确的。泛型函数 area( )的工作方式与 S3 的泛型函数类似，都是根
据输入对象的类执行方法分派。