内置类和方法
S3 泛型函数和方法在统一各种模型的使用方式上是最有用的。例如，我们可以创建一
个线性模型，使用泛型函数从不同角度查看模型信息：
lm1 <- lm(mpg ~ cyl + vs, data = mtcars)
在前面的章节中，我们提到过线性模型本质上是由模型拟合产生的数据字段构成的列表。
这就是为什么 lm1 的类型是 list，但是它的类是 lm，因此泛型函数根据 lm 选择方法：
typeof(lm1)
## [1] "list"
class(lm1)
## [1] "lm"
甚至在没有明确调用 S3 泛型函数时，S3 方法分派也会自动进行。如果我们输入 lm1，
这个模型对象就会被打印出来：
lm1
##
## Call:
## lm(formula = mpg ~ cyl + vs, data = mtcars)
##
## Coefficients:
## (Intercept) cyl vs
## 39.6250 -3.0907 -0.9391
实际上，print( ) 函数被默默地调用了：
print(lm1)
##
## Call:
## lm(formula = mpg ~ cyl + vs, data = mtcars)
##
## Coefficients:
## (Intercept) cyl vs
## 39.6250 -3.0907 -0.9391
我们知道，lm1 本质上是个列表。为什么它被打印出来的时候看起来不太像呢？因为
print( )是个泛型函数，它为 lm 选择了一个方法来打印出线性模型最重要的信息。我们也
可以调用 getS3method("print", "lm") 获取实际用到的方法。事实上，print(lm1)
选择了方法 stats::print.lm，我们可以通过检查它们是否相同来验证：
identical(getS3method("print", "lm"), stats:::print.lm)
## [1] TRUE
注意到，print.lm 是 stats 包中定义的函数，但是没有被导出为公开可见的函数，
所以我们要使用 ::: 来访问它。一般来说，访问包的内部对象是个坏主意，因为它们可能
在不同版本中被更改，而且对用户不可见。在大多数情况下，我们不需要这样做，因为泛
型函数（例如 print( )）会自动选择调用的正确方法。
在 R 中，print( ) 对很多类都有可实现的方法。下面这行代码展示了对于不同的类
print( ) 有多少种实现方法：
length(methods("print"))
## [1] 198
可以调用 methods("print") 查看属于泛型函数 print( ) 的所有方法的列表。实
际上，安装的扩展包越多，这些包中为不同类定义的方法就越多。
print( )展示了模型的一个简要版本，summary( ) 展示更详细的信息。summary( )
也是一个泛型函数，它为模型的所有类提供了许多方法：
summary(lm1)
##
## Call:
## lm(formula = mpg ~ cyl + vs, data = mtcars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.923 -1.953 -0.081 1.319 7.577
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 39.6250 4.2246 9.380 2.77e-10 ***
## cyl -3.0907 0.5581 -5.538 5.70e-06 ***
## vs -0.9391 1.9775 -0.475 0.638
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.248 on 29 degrees of freedom
## Multiple R-squared: 0.7283, Adjusted R-squared: 0.7096
## F-statistic: 38.87 on 2 and 29 DF, p-value: 6.23e-09
线性模型的总结不仅提供了 print( ) 展示的内容，也包括了一些关于系数和模型整
体的重要统计量。实际上，summary( ) 的输出结果也是一个对象，其中包含的数据都可
以被访问。在这个例子中，这个对象（summary( ) 的输出结果）是一个列表，并且是
summary.lm 类的，而且它有可供 print( ) 选择的自己的方法：
lm1summary <- summary(lm1)
typeof(lm1summary)
## [1] "list"
class(lm1summary)
## [1] "summary.lm"
我们可以通过查看列表中的名称，来了解 lm1summary 都包含什么成分：
names(lm1summary)
## [1] "call" "terms" "residuals"
## [4] "coefficients" "aliased" "sigma"
## [7] "df" "r.squared" "adj.r.squared"
##[10] "fstatistic" "cov.unscaled"
访问每个成分的方法与从一个典型列表中提取成分是完全一致的。例如，访问线性模
型的估计系数，我们可以使用 lm1$coefficients。通常使用以下代码访问估计系数：
coef(lm1)
## (Intercept) cyl vs
## 39.6250234 -3.0906748 -0.9390815
这里，coef( )也是一个泛型函数，它从模型对象中提取系数向量。为了访问模型总结
中
详细的系数表格，我们可以使用 lm1summary$coefficients 或者再次使用 coef( )：
coef(lm1summary)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 39.6250234 4.2246061 9.3795782 2.765008e-10
## cyl -3.0906748 0.5580883 -5.5379676 5.695238e-06
## vs -0.9390815 1.9775199 -0.4748784 6.384306e-01
还有一些其他有用的且与模型相关的泛型函数，例如 plot( )、predict( )等。所
有我们提到的泛型函数都是 R 中用户和估计模型交互的标准方式。不同的内置模型和第三
方扩展包提供的模型都能实现这些泛型函数，即它们是通用的，因此我们无需记忆哪些函
数适用于哪个模型。
举个例子，我们可以对线性模型调用 plot( )函数，并且将画布划分成 2 行 2 列，
如图 10-1 所示。
oldpar <- par(mfrow = c(2, 2))
plot(lm1)
par(oldpar)
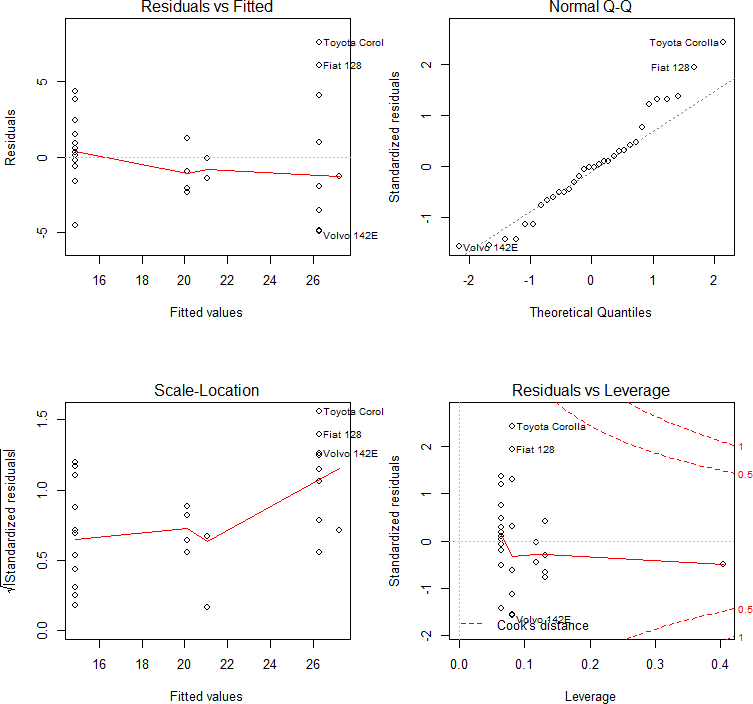
图 10-1
可以看到，我们对线性模型调用 plot( )函数，返回了 4 幅诊断图，用于说明残差的
性质，帮助判断模型拟合的效果。注意到，如果在控制台对 lm 模型直接调用 plot( )，4
幅图会依次交互地完成。为了避免这种情况，我们调用 par( )将绘图区域划分成 2×2 个
子区域。
大多数统计模型都是有用的，因为它们可以利用新数据进行预测，调用 predict( )
加以实现。在这个例子中，我们为 predict( )函数提供线性模型和新数据，泛型函数
predict( )自动选择正确的方法用新数据进行预测：
predict(lm1, data.frame(cyl = c(6, 8), vs = c(1, 1)))
## 1 2
## 20.14189 13.96054
这个函数既可以用在样本内，又可以用在样本外。如果我们为模型提供新数据，
它就进行样本外预测。如果提供样本中的数据，它就进行样本内预测。这里，我们可
以创建一幅关于真实值和拟合值的散点图（见图 10-2），看一看拟合的线性模型的预
测效果：
plot(mtcars$mpg, fitted(lm1))
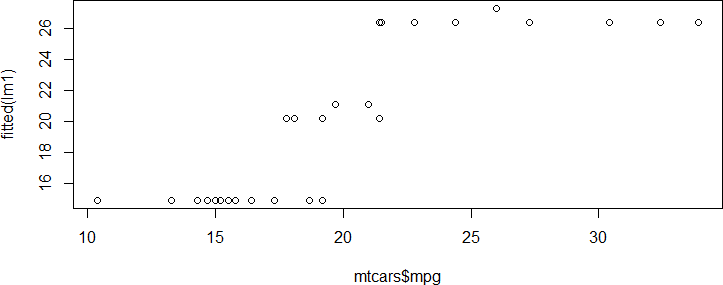
图 10-2
这里，fitted( )也是一个泛型函数，在这个例子中，它等价于lm1$fitted.values，
拟合值等价于用原始数据集得到的预测值，即 predict(lm1, mtcars)。
响应变量的真实值和拟合值的差值称为残差。我们可以使用另一个泛型函数
residuals( )访问残差数值向量，或者等价地使用 lm1$residuals。这里画出残差
的密度曲线图，如图 10-3 所示。
plot(density(residuals(lm1)),
main = "Density of lm1 residuals")
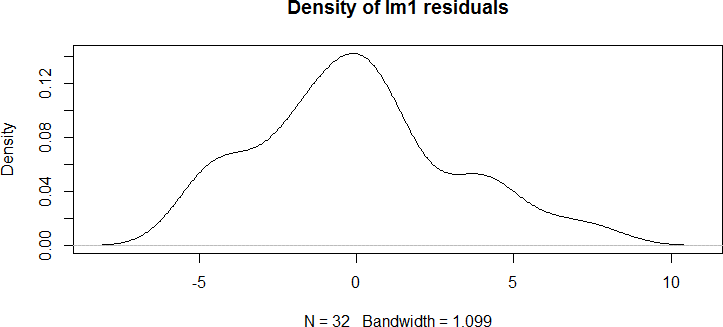
图 10-3
上述函数调用中，所有函数都是泛型函数。residuals( ) 函数从 lm1 中提取残差并返
回一个数值向量。density( ) 函数创建了一个类为 density 的列表，用于存储残差的密度
函数的估计数据。最后，plot( ) 函数选择 plot.density 方法创建一幅密度图。
这些泛型函数不仅适用于 lm、glm 和其他内置模型，也适用于其他扩展包提供的模
型。例如，我们使用 rpart 包，沿用前面例子的数据和公式拟合一个回归树模型。
如果你还没有安装 rpart 包，请先运行以下代码进行安装：
install.packages("rpart")
现在，这个包可以加载了。然后，调用 rpart( ) 函数，而且，调用 rpart( ) 函数
的方式与调用 lm( ) 完全相同：
library(rpart)
tree_model <- rpart(mpg ~cyl + vs, data = mtcars)
我们可以这样做，是因为这个包的作者希望函数调用的方式与调用 R 的内置函数保持
一致。结果对象是一个类为 rpart 的列表，其工作方式与调用 lm( ) 并返回一个类
为 lm 的列表完全相同：
typeof(tree_model)
## [1] "list"
class(tree_model)
## [1] "rpart"
与 lm 对象类似，rpart 对象也有很多可实现的通用方法。例如，我们可以使用
print( ) 函数以它自己的方式将模型打印出来：
print(tree_model)
## n= 32
##
## node), split, n, deviance, yval
## * denotes terminal node
##
## 1) root 32 1126.04700 20.09062
## 2) cyl>= 5 21 198.47240 16.64762
## 4) cyl>= 7 14 85.20000 15.10000 *
## 5) cyl< 7 7 12.67714 19.74286 *
## 3) cyl < 5 11 203.38550 26.66364 *
输出结果显示，对于 rpart，print( )用某种方法简要地展示了这棵回归树的样子。
除了 print( )，summary( )还给出关于模型拟合的更详细的信息：
summary(tree_model)
## Call:
## rpart(formula = mpg ~ cyl + vs, data = mtcars)
## n= 32
##
## CP nsplit rel error xerror xstd
## 1 0.64312523 0 1.0000000 1.0870669 0.25507260
## 2 0.08933483 1 0.3568748 0.4237026 0.08407831
## 3 0.01000000 2 0.2675399 0.4051812 0.08111957
##
## Variable importance
## cyl vs
## 65 35
##
## Node number 1: 32 observations, complexity param=0.6431252
## mean=20.09062, MSE=35.18897
## left son=2 (21 obs) right son=3 (11 obs)
## Primary splits:
## cyl < 5 to the right, improve=0.6431252, (0 missing)
## vs < 0.5 to the left, improve=0.4409477, (0 missing)
## Surrogate splits:
## vs < 0.5 to the left, agree=0.844, adj=0.545, (0 split)
##
## Node number 2: 21 observations, complexity param=0.08933483
## mean=16.64762, MSE=9.451066
## left son=4 (14 obs) right son=5 (7 obs)
## Primary splits:
## cyl < 7 to the right, improve=0.5068475, (0 missing)
## Surrogate splits:
## vs < 0.5 to the left, agree=0.857, adj=0.571, (0 split)
##
## Node number 3: 11 observations
## mean=26.66364, MSE=18.48959
##
## Node number 4: 14 observations
## mean=15.1, MSE=6.085714
##
## Node number 5: 7 observations
## mean=19.74286, MSE=1.81102
同样地，plot( )和 text( )也有方法将 rpart 可视化：
oldpar <- par(xpd = NA)
plot(tree_model)
text(tree_model, use.n = TRUE)
par(oldpar)
然后，我们就得到了树图，如图 10-4 所示。
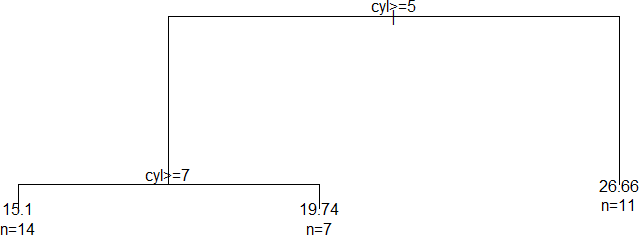
图 10-4
我们可以使用新数据并调用predict( )进行预测，就像在前面线性模型例子中做的一样：
predict(tree_model, data.frame(cyl = c(6, 8), vs = c(1, 1)))
## 1 2
## 19.74286 15.10000
要注意，并非所有的模型对所有的泛型函数都有可实现的方法。例如，由于回归树不
是一个简单的参数模型，所以，对于 coef( )，它就没有相应的实现方法：
coef(tree_model)
## NULL
