ZOJ--3899（分治NTT，DP，线段树）

2015-09-14 22:20:13

【传送门】

题意：有N（有序号）个怪兽，给出M（1～M）个房间，每个房间的初始状态为1，接下来有D次操作，每次操作是选择一个区间使得区间内房间的状态反转（0->1 , 1->0），每次操作后计算将这N个怪兽放进所有状态为1的房间内，且每个状态为1的房间非空的方案数。（注意房间之间不可辨别。两种方案一样，当且仅当两种方案中存在两个房间，里面的怪兽数量以及编号一致）

思路： 根据斯特林数苦思冥想很久没有结果，问了Nero巨巨，才知道应该这么写。。。orz！！（与其展开式有关）

　　核心问题：将n个东西放进k个非空的无序号的盒子中的种数
　　思路：观察到n是不变的，k在变动，令F[i]为n个东西放i个盒子的方案数
　　那么可以这么计算：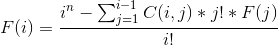
　　大体思路是：先假设有序列性，i^n表示可为空时的方案数，然后减去空的情况
　　 表示n个东西放j(1<=j<i)个有序号盒子的方案数
　　最后再除以 i! 就消去了序列性，变成无序的了。

　　然后转化一下：
　　发现右边是个卷积，就可以分治NTT辣！

　　　（对于状态为1的房间的统计，用线段树就好～） 

#include <cstdio>
#include <ctime>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <vector>
#include <map>
#include <set>
#include <stack>
#include <queue>
#include <string>
#include <iostream>
#include <algorithm>
using namespace std;

#define getmid(l,r) ((l) + ((r) - (l)) / 2)
#define MEM(a,b) memset(a,b,sizeof(a))
#define MP(a,b) make_pair(a,b)
#define PB push_back

typedef long long ll;
typedef pair<int,int> pii;
const double eps = 1e-8;
const int INF = (1 << 30) - 1;

//核心问题：将n个东西放进k个非空的无序号的盒子中的种数
//思路：观察到n是不变的，k在变动，令F[i]为n个东西放i个盒子的方案数
//那么可以这么计算：F[i] = (i^n - Sigma(C(i,j)*j!*F[j])(1<=j<i)) / (i!)
//大体思路是：先假设有序列性，i^n表示可为空时的方案数，然后减去空的情况
//C(i,j)*j!*F[j]表示n个东西放j(1<=j<i)个有序号盒子的方案数
//最后再除以 i! 就消去了序列性，变成无序的了。

//然后转化一下：F[i] = (i^n - i!*Sigma(F[j] / (i-j)!)) / (i!)
//发现右边是个卷积，就可以分治NTT辣！

const int P = 880803841;
const int G = 26;
const int NUM = 30;
const int MAXN = (1 << 18) + 10;

int T,n,m,D;
int rev[MAXN],A1[MAXN],A2[MAXN],wn[2][NUM],inv[MAXN];
int dp[MAXN],fac[MAXN],afac[MAXN];
int t1[MAXN << 2],t0[MAXN << 2],add[MAXN << 2];
int N,bit;

int Q_pow(int x,int y,int mod){
    int res = 1;
    x %= mod;
    while(y){
        if(y & 1) res = 1ll * res * x % mod;
        x = 1ll * x * x % mod;
        y >>= 1;
    }
    return res;
}

void Pre_cal(int n3){
    for(N = 1,bit = 0; N < n3; N <<= 1,++bit);
    for(int i = 1; i < N; ++i)
        rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
}

void NTT(int *A,int n,int f){
    for(int i = 0; i < n; ++i) if(i < rev[i]) swap(A[i],A[rev[i]]);
    int id = (f == -1) ? 1 : 0,p = 1;
    for(int m = 2; m <= n; m <<= 1,++p){
        for(int k = 0; k < n; k += m){
            for(int j = k,w = 1; j < k + (m >> 1); ++j){
                int t = 1ll * w * A[j + (m >> 1)] % P;
                int u = A[j];
                if((A[j] = u + t) >= P) A[j] -= P;
                if((A[j + (m >> 1)] = u - t) < 0) A[j + (m >> 1)] += P;
                w = 1ll * w * wn[id][p] % P;
            }
        }
    }
    if(f == -1) for(int i = 0; i < n; ++i) A[i] = 1ll * A[i] * inv[n] % P;
}

void CDQ(int l,int r){
    if(l == r) return;
    int mid = getmid(l,r);
    CDQ(l,mid);
    int len = r - l + 1;
    Pre_cal(len);
    for(int i = 0; i <= mid - l; ++i) A1[i] = dp[i + l];
    for(int i = mid - l + 1; i < N; ++i) A1[i] = 0;
    for(int i = 0; i < N; ++i) A2[i] = afac[i + 1];
    NTT(A1,N,1);
    NTT(A2,N,1);
    for(int i = 0; i < N; ++i) A1[i] = 1ll * A1[i] * A2[i] % P;
    NTT(A1,N,-1);
    for(int i = mid - l + 1; i <= r - l; ++i) //dp算出来可能为负
        dp[i + l] = ((dp[i + l] - A1[i - 1]) % P + P) % P;
    CDQ(mid + 1,r);
}

void Pre(){
    fac[0] = 1;
    for(int i = 1; i < MAXN; ++i) fac[i] = 1ll * fac[i - 1] * i % P;
    afac[MAXN - 1] = Q_pow(fac[MAXN - 1],P - 2,P);
    for(int i = MAXN - 1; i >= 1; --i) afac[i - 1] = 1ll * afac[i] * i % P;
    for(int i = 1; i < MAXN; ++i) inv[i] = Q_pow(i,P - 2,P);
    for(int i = 0; i < NUM; ++i){
        int t = 1 << i;
        wn[0][i] = Q_pow(G,(P - 1) / t,P);
        wn[1][i] = Q_pow(wn[0][i],P - 2,P);
    }
}

void Solve(int top){
    dp[1] = 1;
    for(int i = 2; i <= top; ++i) dp[i] = 1ll * Q_pow(i,n,P) * afac[i] % P;
    CDQ(1,top);
}

void Push_up(int p){
    t1[p] = t1[p << 1] + t1[p << 1|1];
    t0[p] = t0[p << 1] + t0[p << 1|1];
}

void Build(int p,int l,int r){
    add[p] = 0;
    if(l == r){
        t1[p] = 1;
        t0[p] = 0;
        return;
    }
    int mid = getmid(l,r);
    Build(p << 1,l,mid);
    Build(p << 1|1,mid + 1,r);
    Push_up(p);
}

void Push_down(int p){
    if(add[p]){
        add[p << 1] ^= 1;
        add[p << 1|1] ^= 1;
        swap(t1[p << 1],t0[p << 1]);
        swap(t1[p << 1|1],t0[p << 1|1]);
        add[p] = 0;
    }
}

void Update(int a,int b,int p,int l,int r){
    if(a <= l && r <= b){
        add[p] ^= 1;
        swap(t1[p],t0[p]);
        return;
    }
    Push_down(p);
    int mid = getmid(l,r);
    if(a <= mid) Update(a,b,p << 1,l,mid);
    if(b > mid) Update(a,b,p << 1|1,mid + 1,r);
    Push_up(p);
}

int main(){
    Pre();
    scanf("%d",&T);
    while(T--){
        scanf("%d%d%d",&n,&m,&D);
        Solve(m);
        Build(1,1,m);
        for(int i = 1; i <= D; ++i){
            int a,b;
            scanf("%d%d",&a,&b);
            Update(a,b,1,1,m);
            //ask for dp[t1[1]]
            printf("%d\n",dp[t1[1]]);
        }
    }
    return 0;
}