HDU--5322（分治NTT，DP）

2015-08-17 18:53:54

【传送门】

题意：和 ZOJ3874 那道有点像，题意就不赘述了。

思路：根据DP定义：DP[i]为1～i 排列的答案，那么根据 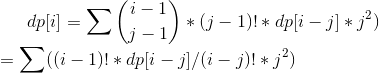就可以CDQ分治NTT来做了。

#include <cstdio>
#include <ctime>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <vector>
#include <map>
#include <set>
#include <stack>
#include <queue>
#include <string>
#include <iostream>
#include <algorithm>
using namespace std;

#define getmid(l,r) ((l) + ((r) - (l)) / 2)
#define MP(a,b) make_pair(a,b)
#define PB push_back

typedef long long ll;
typedef pair<int,int> pii;
const double eps = 1e-8;
const int INF = (1 << 30) - 1;
const int P = 998244353;
const int G = 3;
const int NUM = 20;
const int MAXN = (1 << 18) + 10;

int rev[MAXN];
int A1[MAXN],A2[MAXN],wn[2][NUM];
int fac[MAXN],afac[MAXN],dp[MAXN],sq[MAXN],inv[MAXN];
int n,m,N,bit;

int Q_pow(int x,int y,int mod){
    int res = 1;
    x %= mod;
    while(y){
        if(y & 1) res = 1ll * res * x % mod;
        x = 1ll * x * x % mod;
        y >>= 1;
    }
    return res;
}

void Pre_cal(int n3){
    for(N = 1,bit = 0; N < n3; N <<= 1,++bit); //DFT底层
    for(int i = 1; i < N; ++i)
        rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
    for(int i = 0; i < NUM; ++i){
        int t = 1 << i;
        wn[0][i] = Q_pow(G,(P - 1) / t,P); //预处理求值点
        wn[1][i] = Q_pow(wn[0][i],P - 2,P); //求值点逆元
    }
}

void NTT(int *A,int n,int f){
    for(int i = 0; i < n; ++i) if(i < rev[i]) swap(A[i],A[rev[i]]);
    int id = (f == -1) ? 1 : 0,p = 1;
    for(int m = 2; m <= n; m <<= 1,++p){ //m次单位根
        for(int k = 0; k < n; k += m){ //遍历每一块
            for(int j = k,w = 1; j < k + (m >> 1); ++j){ //折半
                int t = 1ll * w * A[j + (m >> 1)] % P; //右项
                int u = A[j] % P; //左项 (此处取模待商讨)
                if((A[j] = u + t) >= P) A[j] -= P;
                if((A[j + (m >> 1)] = u - t) < 0) A[j + (m >> 1)] += P;
                w = 1ll * w * wn[id][p] % P;
            }
        }
    }
    if(f == -1) for(int i = 0; i < n; ++i) A[i] = 1ll * A[i] * inv[n] % P;
}

void CDQ(int l,int r){
    if(l == r) return;
    int mid = getmid(l,r);
    CDQ(l,mid);
    int len = r - l + 1;
    Pre_cal(len);
    for(int i = 0; i <= mid - l; ++i) A1[i] = (ll)dp[i + l] * afac[i + l] % P;
    for(int i = mid - l + 1; i < N; ++i) A1[i] = 0;
    for(int i = 0; i < N; ++i) A2[i] = sq[i];
    NTT(A1,N,1);
    NTT(A2,N,1);
    for(int i = 0; i < N; ++i) A1[i] = 1ll * A1[i] * A2[i] % P;
    NTT(A1,N,-1);
    for(int i = mid - l + 1; i <= r - l; ++i)
        dp[i + l] = (dp[i + l] + 1ll * A1[i] * fac[i + l - 1] % P) % P;
    CDQ(mid + 1,r);
}

void Solve(){
    fac[0] = 1;
    for(int i = 1; i <= 100000; ++i) fac[i] = 1ll * fac[i - 1] * i % P;
    afac[100000] = Q_pow(fac[100000],P - 2,P);
    for(int i = 100000; i >= 1; --i) afac[i - 1] = 1ll * afac[i] * i % P;
    for(int i = 1; i <= 100000; ++i) sq[i] = 1ll * i * i % P;
    for(int i = 1; i < MAXN; ++i) inv[i] = Q_pow(i,P - 2,P);
    dp[0] = 1;
    CDQ(0,100000);
}

int main(){
    Solve();
    int cur;
    while(scanf("%d",&cur) != EOF){
        printf("%d\n",dp[cur]);
    }
    return 0;
}