CF #252 div2

2014-06-09 22:53:58

A、B依然水过，，（TAT，Ａ题因为数组开小了ＷＡ三次，简直不能再忍！，Ｂ一个小错误给ｈａｃｋ－　－！郁闷的一比）

Ｃ　在最后才Ａ出：按照蛇形输出，前ｋ－１个都输两个ｃｅｌｌ，最后一个输出到底。

#include <cstdio>
#include <iostream>
using namespace std;

int n,m,k,x = 1,y = 1,dir = 1,cnt = 0;

void Next(int &x,int &y){
        if(dir == 1) ++y;
        else --y;
        if(y > m){
            y = m;
            ++x;
            dir = 2;
        }
        if(y < 1){
            y = 1;
            ++x;
            dir = 1;
        }
}

int main(){
    scanf("%d %d %d",&n,&m,&k);
    while(k--){
        if(k == 0){
            printf("%d",n * m - cnt);
            while(1){
                ++cnt;
                printf(" %d %d",x,y);
                Next(x,y);
                if(cnt == n * m)
                    break;
            }
            puts("");
            break;
        }
        cnt += 2;
        printf("2 %d %d",x,y);
        Next(x,y);
        printf(" %d %d\n",x,y);
         Next(x,y);
    }
    return 0;
}

Ｄ：转载一下作者牛牛的思路！：

441D - Valera and Swaps

Problem author dans

In this task you should represent permutation as graph with n vertexes, and from every vertex i exists exactly one edge to vertex p[i]. It's easy to understand that such graph consists of simple cycles only.

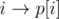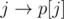If we make swap (i, j), edges  and  will become edges  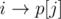and 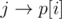 respectively. Then if i and j is in the same cycle, this cycle will break:

but if they are in different cycles, these cycles will merge into one:

this means that every swap operation increases number of cycles by one, or decreases it by one.

Assuming all above, to get permutation q from permutation p, we need to increase (or decrease) number of cycles in p to n - m. Let c— number of cycles in p. Then k always equals |(n - m) - c|.

For satisfying lexicographical minimality we will review three cases:

1) n - m < c

It's easy to understand, that in this case you must decrease cycles number by merging cycles one by one with cycle containing vertex 1. This way every swap has form (1, v), where v > 1. Because every cycle vertex is bigger than previous cycle vertex, this case can be solved with O(n).

2) n - m > c

In this case you should break cycle for every vertex, making swap with smallest possible vertex (it should be in this cycle too). This could be done if represent cycle by line 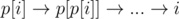. As soon as every cycle is broken with linear asymptotics, this case solution works with O(n2).

Bonus: this way of representing cycle lets us optimize solution to  asymptotics, you may think how.

3) n - m = с

Besause in this case k = 0, there is nothing need to be swapped.

#include <cstdio>
#include <cmath>
#include <cstring>
#include <iostream>
using namespace std;

int n,p[3050],f = 0,m,used[3050];

void Swap(int & a,int &b){
    int tem;
    tem = p[a];
    p[a] = p[b];
    p[b] = tem;
}

int Make_circle(int n){
    int cnt = 0;
    for(int i = n; !used[i]; i = p[i]){
        used[i] = 1;
        ++cnt;
    }
    if(cnt >= 2) return 1;
    else return 0;
}

int main(){
    cin >> n;
    for(int i = 1; i <= n; ++i)
        cin >> p[i];
    cin >> m;
    m = n - m;
    for(int i = 1; i <= n; ++i){
        if(!used[i]){
            ++f;
            Make_circle(i);
        }
    }
    printf("%d\n",(int)abs(f - m));
    memset(used,0,sizeof(used));
    if(m < f){
        Make_circle(1);
        for(int i = 1; i <= n && m < f; ++i){
            if(!used[i]){
                printf("1 %d ",i);
                --f;
                Make_circle(i);
            }
        }
    }
    else if(m > f){
        while(m > f){
            memset(used,0,sizeof(used));
            int flag = 0;
            for(int i = 1; i <= n && m > f; ++i){
                if(Make_circle(i)){
                    for(int j = i + 1; j <= n && m > f; ++j){
                        if(used[j]){
                            printf("%d %d ",i,j);
                            ++f;
                            Swap(i,j);
                            flag = 1;
                            break;
                        }
                    }
                    if(flag) break;
                }
            }    
        }
    }
    puts("");
    return 0;
}