损失函数。

首先我们假设要预测一个公司某商品的销售量：

 

 

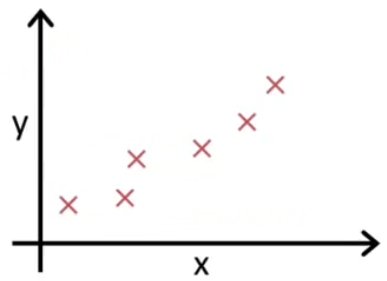
X：门店数     Y：销量

我们会发现销量随着门店数上升而上升。于是我们就想要知道大概门店和销量的关系是怎么样的呢？

我们根据图上的点描述出一条直线：

 

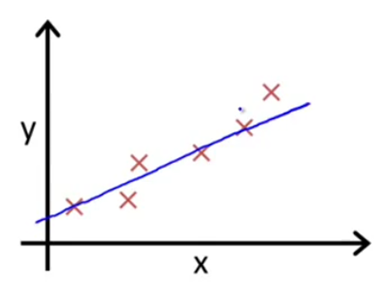
似乎这个直线差不多能说明门店数X和Y得关系了：我们假设直线的方程为Y=a0+a1X（a为常数系数）。假设a0=10 a1=3 那么Y=10+3X（公式1）

X	公式Y	实际Y	差值
1	13	13	0
2	16	14	2
3	19	20	-1
4	22	21	1
5	25	25	0
6	28	30	-2

 

我们希望我们预测的公式与实际值差值越小越好，所以就定义了一种衡量模型好坏的方式，即损失函数（用来表现预测与实际数据的差距程度）。于是乎我们就会想到这个方程的损失函数可以用绝对损失函数表示：

公式Y-实际Y的绝对值，数学表达式：[1]

上面的案例它的绝对损失函数求和计算求得为：6

为后续数学计算方便，我们通常使用平方损失函数代替绝对损失函数：

公式Y-实际Y的平方，数学表达式：L（Y，f（X））= [1]

上面的案例它的平方损失函数求和计算求得为：10

以上为公式1模型的损失值。

假设我们再模拟一条新的直线：a0=8，a1=4

X	公式Y	实际Y	差值
1	12	13	-1
2	16	14	2
3	20	20	0
4	24	21	3
5	28	25	3
6	32	30	2

 

公式2   Y=8+4X

绝对损失函数求和：11  平方损失函数求和：27

公式1   Y=10+3X

绝对损失函数求和：6  平方损失函数求和：10

从损失函数求和中，就能评估出公式1能够更好得预测门店销售。

 

统计学习中常用的损失函数有以下几种：

(1) 0-1损失函数(0-1 lossfunction):

 L(Y,f(X))={1,0,Y≠f(X)Y=f(X)

 (2) 平方损失函数(quadraticloss function)

 L(Y,f(X))=(Y−f(X))2

 (3) 绝对损失函数(absoluteloss function)

 L(Y,f(X))=|Y−f(X)|

 (4) 对数损失函数(logarithmicloss function) 或对数似然损失函数(log-likelihood loss function)

 L(Y,P(Y|X))=−logP(Y|X)

 损失函数越小，模型就越好。